Difference between revisions of "Aufgaben:Exercise 4.3: Iterative Decoding at the BSC"
From LNTwww
| Line 63: | Line 63: | ||
|type="{}"} | |type="{}"} | ||
$\underline{y} = \underline{y}_2 \text{:} \hspace{0.2cm} L_{\rm K}(1) \ = \ ${ 1 3% } | $\underline{y} = \underline{y}_2 \text{:} \hspace{0.2cm} L_{\rm K}(1) \ = \ ${ 1 3% } | ||
| − | $\hspace{1. | + | $\hspace{1.4cm} L_{\rm K}(2) \ = \ ${ -1.03--0.97 } |
| − | $\hspace{1. | + | $\hspace{1.4cm} L_{\rm K}(3) \ = \ ${ 1 3% } |
{Welche Aussagen sind für die Decodierung des Empfangswortes $\underline{y}_2 = (0, \, 1, \, 0)$ zutreffend? Gehen Sie weiterhin vom RC (3, 1, 3) aus. | {Welche Aussagen sind für die Decodierung des Empfangswortes $\underline{y}_2 = (0, \, 1, \, 0)$ zutreffend? Gehen Sie weiterhin vom RC (3, 1, 3) aus. | ||
|type="[]"} | |type="[]"} | ||
+ Ab der ersten Iteration sind alle Vorzeichen von $L_{\rm APP}(i)$ positiv. | + Ab der ersten Iteration sind alle Vorzeichen von $L_{\rm APP}(i)$ positiv. | ||
| − | + Bereits nach der zweiten Iteration ist ${\rm Pr}(\underline{x}_0 | \underline{y}_2)$ größer als $ | + | + Bereits nach der zweiten Iteration ist ${\rm Pr}(\underline{x}_0 | \underline{y}_2)$ größer als $99\%$. |
+ Mit jeder Iteration werden die Beträge $L_{\rm APP}(i)$ größer. | + Mit jeder Iteration werden die Beträge $L_{\rm APP}(i)$ größer. | ||
| Line 76: | Line 76: | ||
- Der iterative Decoder entscheidet richtig. | - Der iterative Decoder entscheidet richtig. | ||
+ Der iterative Decoder entscheidet falsch. | + Der iterative Decoder entscheidet falsch. | ||
| − | + Die „Zuverlässigkeit” für „$\underline{y}_6 | + | + Die „Zuverlässigkeit” für „$\underline{y}_6 \Rightarrow \underline{x}_0$” steigt mit wachsendem $I$. |
</quiz> | </quiz> | ||
Revision as of 09:27, 7 December 2017
Wir betrachten in dieser Aufgabe zwei Codes:
- den Single Parity–Code ⇒ SPC (3, 2, 2):
- $$\underline{x} = \big (\hspace{0.05cm}(0, 0, 0), \hspace{0.1cm} (0, 1, 1), \hspace{0.1cm} (1, 0, 1), \hspace{0.1cm} (1, 1, 0) \hspace{0.05cm} \big ) \hspace{0.05cm}, $$
- den Wiederholungscode ⇒ RC (3, 1, 3:
- $$\underline{x} = \big (\hspace{0.05cm}(0, 0, 0), \hspace{0.1cm} (1, 1, 1) \hspace{0.05cm} \big ) \hspace{0.05cm}.$$
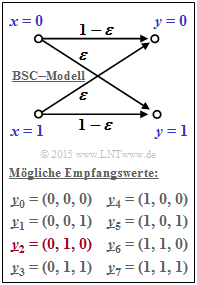
Der Kanal wird auf Bitebene durch das BSC–Modell beschrieben. Entsprechend der Grafik gilt dabei:
- $${\rm Pr}(y_i \ne x_i) \hspace{-0.15cm} \ = \ \hspace{-0.15cm}\varepsilon = 0.269\hspace{0.05cm},$$
- $${\rm Pr}(y_i = x_i) \hspace{-0.15cm} \ = \ \hspace{-0.15cm}1-\varepsilon = 0.731\hspace{0.05cm}.$$
Hierbei bezeichnet $\epsilon$ die Verfälschungswahrscheinlichkeit.
Bis auf die letzte Teilaufgabe wird stets von folgendem Empfangswert ausgegangen:
- $$\underline{y} = (0, 1, 0) =\underline{y}_2 \hspace{0.05cm}. $$
Die hier gewählte Indizierung aller möglichen Empfangsvektoren kann der Grafik entnommen werden. Der meist betrachtete Vektor $\underline{y}_2$ ist hierbei rot hervorgehoben. Für die Teilaufgabe (6) gilt dann:
- $$\underline{y} = (1, 1, 0) =\underline{y}_6 \hspace{0.05cm}. $$
Zur Decodierung sollen in der Aufgabe untersucht werden:
- die Syndromdecodierung, die bei den hier betrachteten Codes als Hard Decision Maximum Likelihood Detection (HD–ML) vornimmt. Hinweis: Softwerte liegen beim BSC nicht vor.
- die symbolweise Soft–in Soft–out Decodierung (SISO) entsprechend dieses Abschnitts.
Hinweise:
- Die Aufgabe bezieht sich auf das Kapitel Soft–in Soft–out Decoder.
- Das vom Decoder ausgewählte Codewort wird in den Fragen mit $\underline{z}$ bezeichnet.
- Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.
Fragebogen
Musterlösung
(1)
(2)
(3)
(4)
(5)