Difference between revisions of "Aufgaben:Exercise 4.08: Repetition to the Convolutional Codes"
From LNTwww
(Die Seite wurde neu angelegt: „{{quiz-Header|Buchseite=Kanalcodierung/Grundlegendes zu den Turbocodes }} [[File:|right|]] ===Fragebogen=== <quiz display=simple> {Multiple-Choic…“) |
|||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite=Kanalcodierung/Grundlegendes zu den Turbocodes | + | {{quiz-Header|Buchseite=Kanalcodierung/Grundlegendes zu den Turbocodes}} |
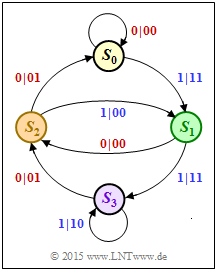
| + | [[File:P_ID3033__KC_A_4_8_v2.png|right|frame|Zustandsübergangsdiagramm eines nichtrekursiven Codes]] | ||
| + | Die Turbocodes basieren auf den Faltungscodes, die im [[Kapitel 3]] auführlich behandelt werden. | ||
| + | Ausgehend von dem nebenstehenden Zustandsübergangsdiagramm sollen wesentliche Eigenschaften und Kenngrößen des betrachteten Rate–1/2–Faltungscodes ermittelt werden, wobei wir ausdrücklich auf folgende Theorieseiten verweisen: | ||
| + | [[Systematische Faltungscodes (1)]] | ||
| + | [[Darstellung im Zustandsübergangsdiagramm (1)]] | ||
| + | [[Definition der freien Distanz (1)]] | ||
| + | [[GF(2)–Beschreibungsformen eines Digitalen Filters (2)]] | ||
| + | [[Anwendung der $D$–Transformation auf Rate–1/n–Faltungscodes (2)]] | ||
| − | }} | + | Im Zustandsübergangsdiagramm wird grundsätzlich vom Zustand $S_0$ ausgegangen. Von jedem Zustand gehen zwei Pfeile ab. Die Beschriftung lautet „$u_i | x_i^{(1)}x_i^{(2)}$”. Bei einem systematischen Code gilt dabei: |
| + | * Das erste Codebit ist identisch mit dem Informationsbit: $x_i^{(1)} = u_i ∈ \{0, \, 1\}$ | ||
| + | * Das zweite Codebit ist das Prüfbit (Paritybit): $x_i^{(2)} = p_i ∈ \{0, \, 1\}$. | ||
| + | |||
| + | |||
| + | ''Hinweise:'' | ||
| + | * Die Aufgabe bezieht sich auf das Kapitel [[...]]. | ||
| + | * Ähnliche Aufgaben finden Sie in den Kapiteln 3.1 bis 3.3. In den Fragen zu dieser Aufgabe werden folgende semi–infinite Vektoren verwendet: | ||
| + | * Informationssequenz $\ \underline{u} = (u_1, \, u_2, \, ...)$, | ||
| + | * Paritysequenz $\ \underline{p} = (p_1, \, p_2, \, ...)$, | ||
| + | * Impulsantwort $\ \underline{g} = (g_1, \, g_2, \, ...)$; diese ist gleich der Paritysequenz $\underline{p}$ für $\underline{u} = (1, \, 0, \, 0, \, ...)$. | ||
| − | |||
===Fragebogen=== | ===Fragebogen=== | ||
| − | |||
<quiz display=simple> | <quiz display=simple> | ||
| − | {Multiple-Choice | + | {Multiple-Choice |
|type="[]"} | |type="[]"} | ||
| − | + | + correct | |
| − | + | + | - false |
| − | |||
{Input-Box Frage | {Input-Box Frage | ||
|type="{}"} | |type="{}"} | ||
| − | $\ | + | $xyz \ = \ ${ 5.4 3% } $ab$ |
| − | |||
| − | |||
| − | |||
</quiz> | </quiz> | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''1 | + | '''(1)''' |
| − | '''2 | + | '''(2)''' |
| − | '''3 | + | '''(3)''' |
| − | '''4 | + | '''(4)''' |
| − | '''5 | + | '''(5)''' |
| − | |||
| − | |||
{{ML-Fuß}} | {{ML-Fuß}} | ||
| − | [[Category:Aufgaben zu Kanalcodierung|^4.3 Grundlegendes zu den Turbocodes | + | [[Category:Aufgaben zu Kanalcodierung|^4.3 Grundlegendes zu den Turbocodes^]] |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | ^]] | ||
Revision as of 19:25, 10 December 2017
Zustandsübergangsdiagramm eines nichtrekursiven Codes
Die Turbocodes basieren auf den Faltungscodes, die im Kapitel 3 auführlich behandelt werden.
Ausgehend von dem nebenstehenden Zustandsübergangsdiagramm sollen wesentliche Eigenschaften und Kenngrößen des betrachteten Rate–1/2–Faltungscodes ermittelt werden, wobei wir ausdrücklich auf folgende Theorieseiten verweisen:
Systematische Faltungscodes (1)
Darstellung im Zustandsübergangsdiagramm (1)
Definition der freien Distanz (1)
GF(2)–Beschreibungsformen eines Digitalen Filters (2)
[[Anwendung der $D$–Transformation auf Rate–1/n–Faltungscodes (2)]]
Im Zustandsübergangsdiagramm wird grundsätzlich vom Zustand $S_0$ ausgegangen. Von jedem Zustand gehen zwei Pfeile ab. Die Beschriftung lautet „$u_i | x_i^{(1)}x_i^{(2)}$”. Bei einem systematischen Code gilt dabei:
- Das erste Codebit ist identisch mit dem Informationsbit: $x_i^{(1)} = u_i ∈ \{0, \, 1\}$
- Das zweite Codebit ist das Prüfbit (Paritybit): $x_i^{(2)} = p_i ∈ \{0, \, 1\}$.
Hinweise:
- Die Aufgabe bezieht sich auf das Kapitel ....
- Ähnliche Aufgaben finden Sie in den Kapiteln 3.1 bis 3.3. In den Fragen zu dieser Aufgabe werden folgende semi–infinite Vektoren verwendet:
- Informationssequenz $\ \underline{u} = (u_1, \, u_2, \, ...)$,
- Paritysequenz $\ \underline{p} = (p_1, \, p_2, \, ...)$,
- Impulsantwort $\ \underline{g} = (g_1, \, g_2, \, ...)$; diese ist gleich der Paritysequenz $\underline{p}$ für $\underline{u} = (1, \, 0, \, 0, \, ...)$.
Fragebogen
Musterlösung
(1)
(2)
(3)
(4)
(5)
