Difference between revisions of "Aufgaben:Exercise 4.08Z: Basics about Interleaving"
| Line 10: | Line 10: | ||
Man unterscheidet allgemein zwischen <font color="#cc0000"><span style="font-weight: bold;">Block–Interleaver</span></font> und <font color="#cc0000"><span style="font-weight: bold;">Random–Interleaver</span></font>. Bei <i>Block–Interleaving</i> füllt man eine Matrix mit $S$ Spalten und $Z$ Zeilen spaltenweise und liest die Matrix zeilenweise aus. Damit wird ein Informationsblock mit $I_{\rm max} = S \cdot Z \ \rm Bit$ deterministisch verwürfelt. | Man unterscheidet allgemein zwischen <font color="#cc0000"><span style="font-weight: bold;">Block–Interleaver</span></font> und <font color="#cc0000"><span style="font-weight: bold;">Random–Interleaver</span></font>. Bei <i>Block–Interleaving</i> füllt man eine Matrix mit $S$ Spalten und $Z$ Zeilen spaltenweise und liest die Matrix zeilenweise aus. Damit wird ein Informationsblock mit $I_{\rm max} = S \cdot Z \ \rm Bit$ deterministisch verwürfelt. | ||
| − | Rechts sind zwei Interleaver angegeben und zwar in grafischer Form durch die Zuordnung $I_{\rm Out}(I_{\rm In})$. Diese Größen stehen für „Index der Ausgangsfolge” bzw. für „Index der Eingangsfolge&rdquo. Es gilt: | + | Rechts sind zwei Interleaver angegeben und zwar in grafischer Form durch die Zuordnung $I_{\rm Out}(I_{\rm In})$. Diese Größen stehen für „Index der Ausgangsfolge” bzw. für „Index der Eingangsfolge”. Es gilt: |
:$$1 \le I_{\rm Out} \le I_{\rm max} \hspace{0.05cm}, \hspace{0.5cm} | :$$1 \le I_{\rm Out} \le I_{\rm max} \hspace{0.05cm}, \hspace{0.5cm} | ||
1 \le I_{\rm In} \le I_{\rm max} \hspace{0.05cm}. $$ | 1 \le I_{\rm In} \le I_{\rm max} \hspace{0.05cm}. $$ | ||
Revision as of 15:46, 11 December 2017
Interleaving (deutsch: Verwürfelung) ist zum Beispiel bei einem Kanal mit Bündelfehlercharakteristik erforderlich, um die Fehler innerhalb des Bündels über einen genügend großen Bereich so zu verteilen, dass diese anschließend weitgehend korrigiert (oder zumindest erkannt) werden können.
Für Turbocodes, die auf RSC–Coder (Recursive Systematic Convolutional Encoder) basieren – und nur solche machen Sinn, ist Interleaving auch beim AWGN–Kanal essentiell, da es dann auch stets (einige) Eingangssequenzen gibt, die in der Ausgangsfolge nach etlichen Einsen nur noch Nullen liefern, und zwar bis ins Unendliche ⇒ es gibt Ausgangsfolgen mit sehr kleinem Hamming–Gewicht.
Verteilt man im Coder 2 die Bits solcher Eingangssequenzen über einen weiten Bereich, so kann bei iterativer symbolweiser Decodierung das Problem durch das Zusammenspiel beider Komponentendecoder (weitgehend) beseitigt werden.
Man unterscheidet allgemein zwischen Block–Interleaver und Random–Interleaver. Bei Block–Interleaving füllt man eine Matrix mit $S$ Spalten und $Z$ Zeilen spaltenweise und liest die Matrix zeilenweise aus. Damit wird ein Informationsblock mit $I_{\rm max} = S \cdot Z \ \rm Bit$ deterministisch verwürfelt.
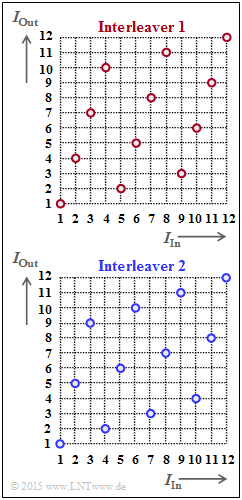
Rechts sind zwei Interleaver angegeben und zwar in grafischer Form durch die Zuordnung $I_{\rm Out}(I_{\rm In})$. Diese Größen stehen für „Index der Ausgangsfolge” bzw. für „Index der Eingangsfolge”. Es gilt:
- $$1 \le I_{\rm Out} \le I_{\rm max} \hspace{0.05cm}, \hspace{0.5cm} 1 \le I_{\rm In} \le I_{\rm max} \hspace{0.05cm}. $$
In der Aufgabe (1) ist gefragt, ob es sich hierbei um Block–Interleaving oder Random Interleaving handelt. Letztere werden im Theorieteil in aller Kürze besprochen.
Hinweise:
- Die Aufgabe bezieht sich auf das Kapitel ....
- Aber auch in anderen LNTwww–Büchern wird Interleaving behandelt, u.A. im Buch „Beispiele von Nachrichtensystemen” mit Bezug zum
- Standard Digital Subscriber Line (DSL) ⇒ Kapitel 3.2,
- 2G–Mobilfunksystem GSM ⇒ Kapitel 3.3,
- 3G–Mobilfunksystem UMTS ⇒ Kapitel 3.4,
- 4G–Mobilfunksystem LTE ⇒ Kapitel 4.3 (im Buch „Mobile Kommunikation”).
Fragebogen
Musterlösung