Aufgaben:Exercise 2.2: Properties of Galois Fields

• Return to book

Additions– und Multiplikationstabellen für $q = 5$ und $q = 6$

Wir betrachten hier die Zahlenmengen

• $Z_5 = \{0, \, 1, \, 2, \, 3, \, 4\} \ \Rightarrow \ q = 5$,
• $Z_6 = \{0, \, 1, \, 2, \, 3, \, 4,\, 5\} \ \Rightarrow \ q = 6$.

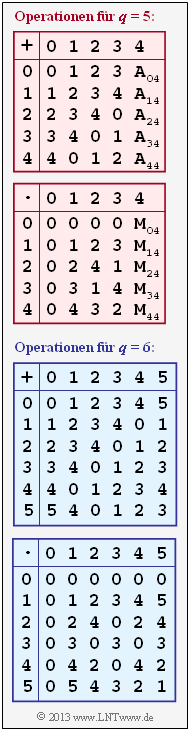
In nebenstehender Grafik sind die (teilweise unvollständigen) Additions– und Multiplikationstabellen für $q = 5$ und für $q = 6$ angegeben, wobei sowohl die Addition („$+$”) als auch die Multiplikation („$\cdot$”) modulo $q$ zu verstehen sind.

Zu überprüfen ist, ob die Zahlenmengen $Z_5$ und $Z_6$ alle Bedingungen eines Galoisfeldes $\rm GF(5)$ bzw. $\rm GF(6)$ erfüllen. Im Theorieteil werden insgesamt acht Bedingungen genannt, die alle erfüllt sein müssen. Von Ihnen überprüft werden sollen nur zwei dieser Bedingungen:

(D) Für alle Elemente gibt es eine additive Inverse (Inverse for „$+$”):

$$\forall \hspace{0.15cm} z_i \in {\rm GF}(q),\hspace{0.15cm} \exists \hspace{0.15cm} {\rm Inv_A}(z_i) \in {\rm GF}(q):$$

$$\hspace{0.25cm}z_i + {\rm Inv_A}(z_i) = 0 \hspace{0.25cm} \Rightarrow \hspace{0.25cm} {\rm Inv_A}(z_i) = -z_i \hspace{0.05cm}.$$

(E) Alle Elemente haben eine multiplikative Inverse (Inverse for „$\cdot$”):

$$\forall \hspace{0.15cm} z_i \in {\rm GF}(q),\hspace{0.15cm} z_i \ne 0, \hspace{0.15cm} \exists \hspace{0.15cm} {\rm Inv_M}(z_i) \in {\rm GF}(q):$$

$$\hspace{0.25cm}z_i \cdot {\rm Inv_M}(z_i) = 1 \hspace{0.25cm} \Rightarrow \hspace{0.25cm} {\rm Inv_M}(z_i) = z_i^{-1}\hspace{0.05cm}.$$

Die weiteren Bedingungen für ein Galoisfeld, nämlich

• Closure,
• Existenz von Null– und Einselelement,
• Gültigkeit von Kommutativ–, Assoziativ– und Distributivgesetz

werden sowohl von $Z_5$ als auch von $Z_6$ erfüllt.

Hinweis:

• Die Aufgabe bezieht sich auf das Kapitel Einige Grundlagen der Algebra.
• Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.

Fragebogen

1

Ergänzen Sie die Additionstabelle für $q = 5$. Geben Sie folgende Werte ein:

$A_{04} \ = \ $

$A_{14} \ = \ $

$A_{44} \ = \ $

2

Ergänzen Sie die Multiplikationstabelle für $q = 5$. Geben Sie folgende Werte ein:

$M_{04} \ = \ $

$M_{14} \ = \ $

$M_{44} \ = \ $

3

Erfüllt die Menge $Z_5$ die Bedingungen eines Galoisfeldes?

	Ja.
	Nein, es gibt nicht für alle Elemente $(0 \ - \ 4)$ eine additive Inverse.
	Nein, die Elemente $1-4$ haben nicht alle eine multiplikative Inverse.

4

Erfüllt die Menge $Z_6$ die Bedingungen eines Galoisfeldes?

	Ja.
	Nein, es gibt nicht für alle Elemente $(0 \ - \ 5)$ eine additive Inverse.
	Nein, die Elemente $1-5$ haben nicht alle eine multiplikative Inverse.

5

Die Zahlenmengen $Z_2, \ Z_3, \ Z_5$ und $Z_7$ ergeben ein Galoisfeld, die Mengen $Z_4, \ Z_6, \ Z_8, \ Z_9$ dagegen nicht. Was folgern Sie daraus?

	$Z_{10} = \{0, \, 1, \, 2, \, 3, \, 4, \, 5, \, 6, \, 7, \, 8, \, 9\}$ ist ein Galoisfeld?
	$Z_{11} = \{0, \, 1, \, 2, \, 3, \, 4, \,5, \, 6, \, 7, \, 8, \, 9, \, 10\}$ ist ein Galoisfeld?
	$Z_{12} = \{0, \, 1, \, 2, \, 3, \, 4, \, 5, \, 6, \, 7, \, 8, \, 9, \, 10, \, 11\}$ ist ein Galoisfeld?

Musterlösung

Solution

(1) 

(2) 

(3) 

(4) 

(5)