Aufgaben:Exercise 2.11Z: Erasure Channel for Symbols

• Return to book

Auslöschungskanal für Symbole: $m$–BEC

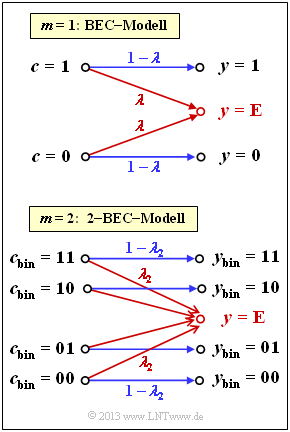
Das Kanalmodell Binary Erasure Channel (BEC) beschreibt einen Auslöschungskanal auf Bitebene. Ein Binärsymbol $0$ bzw. $1$ wird mit der Wahrscheinlichkeit $1 - \lambda$ richtig übertragen und mit der Wahrscheinlichkeit $\lambda$ als Auslöschung $\rm E$ (Erasure) markiert. Im Gegensatz zum BSC kann es hier nicht zu Verfälschungen $(0 → 1, \ 1 → 0)$ kommen.

Ein Reed–Solomon–Code basiert auf einem Galoisfeld ${\rm GF}(2^m)$ mit ganzzahligem $m$. Jedes Codesymbol $c$ lässt sich somit durch $m \ \rm Bit$ darstellen. Will man hier das BEC–Modell anwenden, so muss man dieses zum m–BEC–Modell modifizieren, wie es in der unteren Grafik für $m = 2$ gezeigt ist:

Alle Codesymbole – in binärer Darstellung $00, \ 01, \ 10$ und $11$ – werden mit der Wahrscheinlichkeit $1 - \lambda_2$ richtig übertragen. Damit beträgt die Wahrscheinlichkeit für ein ausgelöschtes Symbol $\lambda_2$. Zu beachten ist, dass bereits ein einziges ausgelöschtes Bit zum ausgelöschten Empfangssymbol $y = \rm E$ führt.

Hinweise:

• Die Aufgabe gehört zum Kapitel Reed–Solomon–Decodierung beim Auslöschungskanal.
• Bei einem auf ${\rm GF}(2^m)$ basierenden Code ist das skizzierte 2–BEC–Modell zum $m$–BEC zu erweitern. Die Auslöschungswahrscheinlichkeit dieses Modell wird dann mit $\lambda_m$ bezeichnet.
• Für die Teilaufgaben (1), (2) und (3) gelte für die Auslöschungswahrscheinlichkeit des Grundmodells gemäß der oberen Grafik stets $\lambda = 0.2$.
• Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.

Fragebogen

1

Es gelte $\lambda = 0.2$. Mit welchen Wahrscheinlichkeiten treten beim BEC–Modell die möglichen Empfangswerte auf?

$1-{\rm BEC} \text{:} \hspace{0.2cm} {\rm Pr}(y = 0) \ = \ $

$\hspace{1.2cm} {\rm Pr}(y = {\rm E}) \ = \ $

$\hspace{1.2cm} {\rm Pr}(y = {\rm 1}) \ = \ $

2

Wie groß ist die Auslöschungswahrscheinlichkeit $\lambda_2$ auf Symbolebene, wenn der Reed–Solomon–Code auf $\rm GF(2^2)$ basiert $(\lambda = 0.2)$?

$2–{\rm BEC} \text{:} \hspace{0.2cm} \lambda_2 \ = \ $

3

Wie groß ist die Auslöschungswahrscheinlichkeit $\lambda_m$, wenn das $m$–BEC–Modell an den $\rm RSC \, (255, \, 223, \, 33)_{256}$ angepasst wird $(\lambda = 0.2)$?

$m–{\rm BEC} \text{:} \hspace{0.2cm} \lambda_m \ = \ $

4

Wie groß darf die Auslöschungswahrscheinlichkeit $\lambda$ beim Grundmodell (BEC) maximal sein, damit $\lambda_m ≤ 0.2$ gilt?

$\lambda_m ≤ 0.2 \text{:} \hspace{0.2cm} {\rm Max}[\lambda] \ = \ $

5

Mit welcher Wahrscheinlichkeit wird damit das „Nullsymbol” empfange?

$\lambda_m = 0.2 \text{:} \hspace{0.2cm} {\rm Pr}(y_{\rm bin} = 00000000) \ = \ $

Musterlösung

Solution

(1)  (2)  (3)  (4)  (5)