Aufgaben:Exercise 4.7: About the Rake Receiver

• Return to book

Zweiwegekanal und RAKE–Empfänger

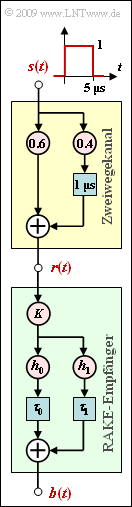
Die Grafik zeigt einen Zweiwegekanal (gelbe Hinterlegung). Die entsprechende Beschreibungsgleichung lautet:

$$r(t) =0.6 \cdot s(t) + 0.4 \cdot s (t - \tau) \hspace{0.05cm}.$$

Die Verzögerung auf dem Nebenpfad sei $\tau = 1 \ \rm \mu s$. Darunter gezeichnet ist die Struktur eines RAKE–Empfängers (grüne Hinterlegung) mit den allgemeinen Koeffizienten $K, h_{0}, h_{1}, \tau_{0}$ und $\tau_{1}$.

Der RAKE–Empfänger hat die Aufgabe, die Energie der beiden Signalpfade zu bündeln und dadurch die Entscheidung sicherer zu machen. Die gemeinsame Impulsantwort von Kanal und RAKE–Empfänger kann in der Form

$$h_{\rm KR}(t) = A_0 \cdot \delta (t ) + A_1 \cdot \delta (t - \tau) + A_2 \cdot \delta (t - 2\tau)$$

angegeben werden, allerdings nur dann, wenn die RAKE–Koeffizienten $h_{0}, h_{1}, \tau_{0}$ und $\tau_{1}$ geeignet gewählt werden. Der Hauptanteil von $h_{\rm KR}(t)$ soll bei $t = \tau$ liegen.

Die Konstante $K$ ist aus Normierungsgründen notwendig. Um den Einfluss von AWGN–Rauschen nicht zu verfälschen, muss folgende Bedingung erfüllt sein:

$$K= \frac{1}{h_0^2 + h_1^2}.$$

Gesucht sind außer den geeigneten RAKE–Parametern auch die Signale $r(t)$ und $b(t)$, wenn $s(t)$ ein Rechteck der Höhe $1$ und der Breite $T = 5 \ \rm \mu s$ ist.

Hinweis:

Die Aufgabe bezieht sich auf Nachrichtentechnische Aspekte von UMTS dieses Buches sowie auf Untersuchungen zum RAKE–Empfänger von Fehlerwahrscheinlichkeit der PN–Modulation im Buch „Modulationsverfahren”.

Fragebogen

1

Welche Aussagen gelten für die Kanalimpulsantwort $h_{\rm K}(t)$?

	$h_{\rm K}(t)$ besteht aus zwei Diracfunktionen.
	$h_{\rm K}(t)$ ist komplexwertig.
	$h_{\rm K}(t)$ ist eine mit der Verzögerungszeit $\tau$ periodische Funktion.

2

Welche Aussagen gelten für den Kanalfrequenzgang $H_{\rm K}(f)$?

	Es gilt $H_{\rm K}(f = 0) = 2$.
	$H_{\rm K}(f)$ ist komplexwertig.
	$H_{\rm K}(f)$| ist eine mit der Frequenz $1/ \tau$ periodische Funktion.

3

Setzen Sie $K = 1, h_{0} = 0.6$ und $h_{1} = 0.4$. Bestimmen Sie die Verzögerungen $\tau_{0}$ und $\tau_{1}$, damit die $h_{\rm KR}(t)$–Gleichung mit $A_{0} = A_{2}$ erfüllt wird.

$\tau_{0} \ = \ $ $\ \rm \mu s$

$\tau_{1} \ = \ $ $\ \rm \mu s$

4

Welcher Wert ist für die Konstante $K$ zu wählen?

$K \ = \ $

5

Welche Aussagen gelten für die Signale $r(t)$ und $b(t)$?

	Der Maximalwert von $r(t)$ ist $1$.
	Die Breite von $r(t)$ ist $7 \ \rm \mu s$.
	Der Maximalwert von $b(t)$ ist $1 \ \rm \mu s$.
	Die Breite von $b(t)$ ist $7 \ \rm \mu s$.

Musterlösung

Solution

(1) 

(2) 

(3) 

(4) 

(5)