Difference between revisions of "Aufgaben:Exercise 2.15: Block Error Probability with AWGN"
| Line 24: | Line 24: | ||
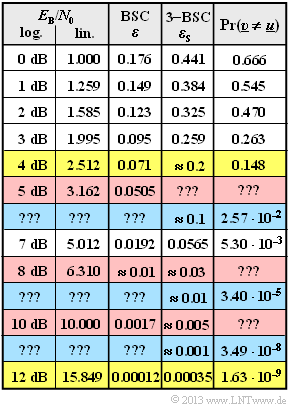
Für einige $E_{\rm B}/N_0$–Werte sind alle Ergebnisse bereits in obiger Tabelle eingetragen. Die gelb hinterlegten Zeilen werden hier kurz erläutert. | Für einige $E_{\rm B}/N_0$–Werte sind alle Ergebnisse bereits in obiger Tabelle eingetragen. Die gelb hinterlegten Zeilen werden hier kurz erläutert. | ||
* Für $10 \cdot \lg {E_{\rm B}/N_0} = 4 \ \rm dB$ ergibt sich $\epsilon \approx {\rm Q}(1.47) \approx 0.071$ und $\epsilon_{\rm S} \approx 0.2$. Der einfachste Weg zur Berechnung der Blockfehlerwahrscheinlichkeit führt hier über das Kompliment: | * Für $10 \cdot \lg {E_{\rm B}/N_0} = 4 \ \rm dB$ ergibt sich $\epsilon \approx {\rm Q}(1.47) \approx 0.071$ und $\epsilon_{\rm S} \approx 0.2$. Der einfachste Weg zur Berechnung der Blockfehlerwahrscheinlichkeit führt hier über das Kompliment: | ||
| + | :$${\rm Pr(Blockfehler)} = 1 - \big [ {7 \choose 0} \cdot 0.8^7 + {7 \choose 1} \cdot 0.2 \cdot 0.8^6 + {7 \choose 2} \cdot 0.2^2 \cdot 0.8^5\big ] | ||
| + | \approx 0.148 \hspace{0.05cm}.$$ | ||
| + | * Für $10 \cdot \lg {E_{\rm B}/N_0} = 12 \ \rm dB$ erhält man $\epsilon \approx 1.2 \cdot 10^{-4}$ und $\epsilon_{\rm S} \approx 3.5 \cdot 10^{-4}$. Mit dieser sehr kleinen Verfälschungswahrscheinlichkeit dominiert der $f = 3$–Term und man erhält | ||
| + | :$${\rm Pr(Blockfehler)} \approx {7 \choose 3} \cdot (3.5 \cdot 10^{-4})^3 \cdot (1- 3.5 \cdot 10^{-4})^4 | ||
| + | \approx 1.63 \cdot 10^{-9} \hspace{0.05cm}.$$ | ||
| + | |||
| + | In dieser Aufgabe sollen Sie für die rot hinterlegten Zeilen $(10 \cdot \lg {E_{\rm B}/N_0} = 5 \ \rm dB, \ 8 \ dB$ und $10 \ \rm dB$) die Blockfehlerwahrscheinlichkeiten berechnen. | ||
| + | |||
| + | Die blau hinterlegten Zeilen zeigen einige Ergebnisse der [[Zusatzaufgabe Z2.15]]. Dort wird ${\rm Pr}(\underline{\upsilon} ≠ \underline{u})$ für $\epsilon_{\rm S} = 10\%$ und $0.1\%$ berechnet. In den Teilaufgaben (4) und (5) sollen Sie den Zusammenhang zwischen dieser Größe $\epsilon_{\rm S}$ und dem AWGN–Parameter $E_{\rm B}/N_0$ herstellen und somit die obige Tabelle vervollständigen. | ||
| + | |||
| + | ''Hinweise:'' | ||
| + | * Die Aufgabe gehört zum Kapitel [[...]]. | ||
| + | * Wir weisen Sie auf folgeende Interaktionsmodule hin: | ||
| + | # [[Komplementäre Gaußsche Fehlerfunktionen]] | ||
| + | # [[Wahrscheinlichkeiten der Binomialverteilung]] | ||
| + | |||
| + | |||
Revision as of 21:24, 18 December 2017
Am Beispiel des $\rm RSC \, (7, \, 3, \, 5)_8$ mit den Parametern
- $n = 7$ (Anzahl der Codesymbole),
- $k =3$ (Anzahl der Informationssymbole),
- $t = 2$ (Korrekturfähigkeit)
soll die Berechnung der Blockfehlerwahrscheinlichkeit beim Bounded Distance Decoding (BDD) gezeigt werden. Die entsprechende Gleichung lautet:
- $${\rm Pr(Blockfehler)} =$$
- $$ = \sum_{f = t + 1}^{n} {n \choose f} \cdot {\varepsilon_{\rm S}}^f \cdot (1 - \varepsilon_{\rm S})^{n-f} \hspace{0.05cm}.$$
Die Berechnung erfolgt für den AWGN–Kanal, der durch den Parameter $E_{\rm B}/N_0$ gekennzeichnet ist. Dieser Quotient lässt sich über die Beziehung
- $$\varepsilon = {\rm Q} \big (\sqrt{\frac{2 \cdot R \cdot E_{\rm B}}{N_0}} \big ) $$
in das BSC–Modell übeführen, wobei $R$ die Coderate bezeichnet (hier: $R = 3/7$) und ${\rm Q}(x)$ und Komplementäre Gaußsche Fehlerintegral angibt. Da aber beim betrachteten Code die Symbole aus $\rm GF(2^3)$ entstammen, muss das BSC–Modell mit Parameter $\epsilon$ ebenfalls noch an die Aufgabenstellung adaptiert werden. Für die Verfälschungwahrscheinlichkeit des M–BSC–Modells gilt:
- $$\varepsilon_{\rm S} = 1 - (1 - \varepsilon)^m \hspace{0.05cm},$$
wobei hier $m = 3$ zu setzen ist (3 Bit pro Codesymbol).
Für einige $E_{\rm B}/N_0$–Werte sind alle Ergebnisse bereits in obiger Tabelle eingetragen. Die gelb hinterlegten Zeilen werden hier kurz erläutert.
- Für $10 \cdot \lg {E_{\rm B}/N_0} = 4 \ \rm dB$ ergibt sich $\epsilon \approx {\rm Q}(1.47) \approx 0.071$ und $\epsilon_{\rm S} \approx 0.2$. Der einfachste Weg zur Berechnung der Blockfehlerwahrscheinlichkeit führt hier über das Kompliment:
- $${\rm Pr(Blockfehler)} = 1 - \big [ {7 \choose 0} \cdot 0.8^7 + {7 \choose 1} \cdot 0.2 \cdot 0.8^6 + {7 \choose 2} \cdot 0.2^2 \cdot 0.8^5\big ] \approx 0.148 \hspace{0.05cm}.$$
- Für $10 \cdot \lg {E_{\rm B}/N_0} = 12 \ \rm dB$ erhält man $\epsilon \approx 1.2 \cdot 10^{-4}$ und $\epsilon_{\rm S} \approx 3.5 \cdot 10^{-4}$. Mit dieser sehr kleinen Verfälschungswahrscheinlichkeit dominiert der $f = 3$–Term und man erhält
- $${\rm Pr(Blockfehler)} \approx {7 \choose 3} \cdot (3.5 \cdot 10^{-4})^3 \cdot (1- 3.5 \cdot 10^{-4})^4 \approx 1.63 \cdot 10^{-9} \hspace{0.05cm}.$$
In dieser Aufgabe sollen Sie für die rot hinterlegten Zeilen $(10 \cdot \lg {E_{\rm B}/N_0} = 5 \ \rm dB, \ 8 \ dB$ und $10 \ \rm dB$) die Blockfehlerwahrscheinlichkeiten berechnen.
Die blau hinterlegten Zeilen zeigen einige Ergebnisse der Zusatzaufgabe Z2.15. Dort wird ${\rm Pr}(\underline{\upsilon} ≠ \underline{u})$ für $\epsilon_{\rm S} = 10\%$ und $0.1\%$ berechnet. In den Teilaufgaben (4) und (5) sollen Sie den Zusammenhang zwischen dieser Größe $\epsilon_{\rm S}$ und dem AWGN–Parameter $E_{\rm B}/N_0$ herstellen und somit die obige Tabelle vervollständigen.
Hinweise:
- Die Aufgabe gehört zum Kapitel ....
- Wir weisen Sie auf folgeende Interaktionsmodule hin:
Fragebogen
Musterlösung