Difference between revisions of "Applets:Lineare Verzerrungen periodischer Signale"
m (Guenter verschob die Seite Lineare Verzerrungen Versuchsdurchführung nach Lineare Verzerrungen periodischer Signale) |
|||
| Line 122: | Line 122: | ||
| − | $\hspace{1.0cm}\Rightarrow\hspace{0.3cm} \text{Bestmögliche Anpassung:} \hspace{0.2cm}k_{\rm M}\hspace{0.15cm}\underline{ = 2.06} \text{ | + | $\hspace{1.0cm}\Rightarrow\hspace{0.3cm} \text{Dämpfungs- und Phasenverzerrungen. Bestmögliche Anpassung:} \hspace{0.2cm}k_{\rm M}\hspace{0.15cm}\underline{ = 2.06} \text{, } \tau_{\rm M}\hspace{0.15cm}\underline{ = 0.15\ {\rm ms} }\text{:} \hspace{0.2cm}P_{\rm D} = 0.136 \ {\rm V^2},\hspace{0.1cm}\rho_{\rm D} \approx 3.7$. |
| − | $\hspace{1.85cm}\text{ | + | $\hspace{1.85cm}\text{Zusammenfassen von }\varphi \text{- und } \tau\text{-Parameter: } y(t) = 0.4 \ {\rm V} \cdot \sin\ (2\pif_1 t) - 0.12 \ {\rm V} \cdot \sin\ (2\pi \cdot 3f_1\cdot t) \approx 0.52 \ {\rm V} \cdot \sin^3(2\pi f_1 t)$. |
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | '''( | + | '''(9)''' Für das Sendesignal $x(t)$ gelte nun $A_1 = A_2 = 1\ {\rm V}, \ f_1 = 1\ {\rm kHz}, \ f_2 = 1\ {\rm kHz}, \ \varphi_1 = 0^\circ, \ \varphi_2 = 0^\circ$ und der Kanal ein Tiefpass erster Ordnung $(f_0 = 2\ {\rm kHz})$. Wählen Sie die letzte Einstellung ⇒ „Recall Parameters” und ändern Sie $f_2' = 0.6$. Speichern Sie diese Einstellung mit „Store Parameters”:}} |
$\hspace{1.0cm}\Rightarrow\hspace{0.3cm}$Die Periodendauer ist $T_0 = 5.0 \ \rm ms$ wegen ${\rm ggt}(0.2,0.6) = 0.2$. | $\hspace{1.0cm}\Rightarrow\hspace{0.3cm}$Die Periodendauer ist $T_0 = 5.0 \ \rm ms$ wegen ${\rm ggt}(0.2,0.6) = 0.2$. | ||
| Line 135: | Line 135: | ||
$\hspace{1.0cm}\Rightarrow\hspace{0.3cm}$Der maximale Signalwert ist $x_{\rm max} =x(t_* + i \cdot T_0) = 1.39 \ \rm V$ mit $t_* = 0.3 \ \rm ms$ und $T_0 = 5.0 \ \rm ms$ | $\hspace{1.0cm}\Rightarrow\hspace{0.3cm}$Der maximale Signalwert ist $x_{\rm max} =x(t_* + i \cdot T_0) = 1.39 \ \rm V$ mit $t_* = 0.3 \ \rm ms$ und $T_0 = 5.0 \ \rm ms$ | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| Line 187: | Line 180: | ||
==Nochmalige Aufrufmöglichkeit des Applets in neuem Fenster== | ==Nochmalige Aufrufmöglichkeit des Applets in neuem Fenster== | ||
| − | {{LntAppletLink| | + | {{LntAppletLink|verzerrungen}} |
[[Category:Applets|^Periodendauer^]] | [[Category:Applets|^Periodendauer^]] | ||
Revision as of 16:17, 11 January 2018
Contents
Programmbeschreibung
Dieses Applet veranschaulicht die Auswirkungen von linearen Verzerrungen (Dämpfungsverzerrungen und Phasenverzerrungen) anhand
- des Eingangssignals $x(t) = x_1(t) + x_2(t) = A_1\cdot \cos\left(2\pi f_1\cdot t- \varphi_1\right)+A_2\cdot \cos\left(2\pi f_2\cdot t- \varphi_2\right)\hspace{0.3cm}\Rightarrow\hspace{0.3cm}\text{Leistung }P_x, $
- des Ausgangssignals $y(t) = \alpha_1 \cdot x_1(t-\tau_1) + \alpha_2 \cdot x_2(t-\tau_2)\hspace{0.3cm}\Rightarrow\hspace{0.3cm}\text{Leistung }P_y,$
- des Matching–Ausgangssignals $z(t) = k_{\rm M} \cdot y(t-\tau_{\rm M}) + \alpha_2 \cdot x_2(t-\tau_2)\hspace{0.3cm}\Rightarrow\hspace{0.3cm}\text{Leistung }P_z,$ und
- des Differenzsignals $\varepsilon(t) = z(t) - x(t)\hspace{0.3cm}\Rightarrow\hspace{0.3cm}\text{Leistung }P_\varepsilon.$
Die Amplituden– und Phasenanpassung des Ausgangssignals $y(t)$ ⇒ „Matching” erlaubt die Unterscheidung
- zwischen einer Dämpfungsverzerrung und einer frequenzunabhängigen Dämpfung, sowie
- zwischen einer Phasenverzerrung und einer reinen Laufzeit.
Als Maß für die Stärke der linearen Verzerrungen wird die Verzerrungsleistung (englisch: Distortion Power) $P_{\rm D}$ ausgegeben.
Theoretischer Hintergrund
Lineare Verzerrungen treten üblicherweise in Form von
- Dämpfungsverzerrungen $\alpha_i$ und
- Phasenverzerrungen $\tau_i$ auf.
Ist $\alpha_1 \ne \alpha_2$ und $\tau_1 = \tau_2$, so liegen ausschließlich Dämpfungsverzerrungen vor.
Dagegen führt $\alpha_1 = \alpha_2$ und $\tau_1 \ne \tau_2$ zu reinen Phasenverzerrungen.
Ein Signal $y(t)$ ist gegenüber $x(t)$ unverzerrt, wenn $\alpha_1 = \alpha_2$ und $\tau_1 und \tau_2$ gilt.
$\text{Berechnungsvorschrift:}$ Setzt sich das periodisches Signal $x(t)$ wie in diesem Applet aus zwei Anteilen $x_1(t)$ und $x_2(t)$ zusammen, dann gilt mit $A_1 \ne 0$, $f_1 \ne 0$, $A_2 \ne 0$, $f_2 \ne 0$ für Grundfrequenz und Periodendauer:
- $$f_0 = {\rm ggT}(f_1, \ f_2) \hspace{0.3cm} \Rightarrow \hspace{0.3cm}T_0 = 1/f_0,$$
wobei „ggT” den größten gemeinsamen Teiler bezeichnet.
$\text{Beispiele:}$ Im Folgenden bezeichnen $f_0'$, $f_1'$ und $f_2'$ die auf $1\ \rm kHz$ normierten Signalfrequenzen:
(a) $f_1' = 1.0$, $f_2' = 3.0$ ⇒ $f_0' = {\rm ggt}(1.0, \ 3.0) = 1.0$ ⇒ $T_0 = 1.0\ \rm ms$;
(b) $f_1' = 1.0$, $f_2' = 3.5$ ⇒ $f_0' = {\rm ggt}(1.0, \ 3.5)= 0.5$ ⇒ $T_0 = 2.0\ \rm ms$;
(c) $f_1' = 1.0$, $f_2' = 2.5$ ⇒ $f_0' = {\rm ggt}(1.0, \ 2.5) = 0.5$ ⇒ $T_0 = 2.0\ \rm ms$;
(d) $f_1' = 0.9$, $f_2' = 2.5$ ⇒ $f_0' = {\rm ggt}(0.9, \ 2.5) = 0.1$ ⇒ $T_0 = 10.0 \ \rm ms$;
(e) $f_2' = \sqrt{2} \cdot f_1' $ ⇒ $f_0' = {\rm ggt}(f_1', \ f_2') \to 0$ ⇒ $T_0 \to \infty$ ⇒ Das Signal $x(t)$ ist nicht periodisch.
$\text{Anmerkung:}$ Die Periodendauer könnte auch als kleinstes gemeinsame Vielfache (kgV) entsprechend $T_0 = {\rm kgV}(T_1, \ T_2)$ ermittelt werden:
(c) $T_1 = 1.0\ \rm ms$, $T_2 = 0.4\ \rm kHz$ ⇒ $T_0 = {\rm kgV}(1.0, \ 0.4) \ \rm ms = 2.0\ \rm ms$
Bei allen anderen Parameterwerten würde es aber zu numerischen Problemen kommen, zum Beispiel
(a) $T_1 = 1.0\ \rm ms$ und $T_2 = 0.333\text{...} \ \rm ms$ besitzen aufgrund der begrenzten Darstellung reeller Zahlen kein kleinstes gemeinsames Vielfaches.
Vorschlag für die Versuchsdurchführung
BlaBla
(1) Für das Sendesignal $x(t)$ gelte $A_1 = 0.8\ {\rm V}, \ A_2 = 0.6\ {\rm V}, \ f_1 = 0.5\ {\rm kHz}, \ f_2 = 1.5\ {\rm kHz}, \ \varphi_1 = 90^\circ, \ \varphi_2 = 0^\circ$.
- Wie groß ist die Periodendauer $T_0$? Welche Leistung $P_x$ weist dieses Signal auf? Wo können Sie diesen Wert im Programm ablesen?
$\hspace{1.0cm}\Rightarrow\hspace{0.3cm}T_0 = \big [\hspace{-0.1cm}\text{ größter gemeinsamer Teiler }(0.5 \ {\rm kHz}, \ 1.5 \ {\rm kHz})\big ]^{-1} = 2.0 \ {\rm ms};$
$\hspace{1.85cm} P_x = A_1^2/2 + A_2^2/2 = 0.5 \ {\rm V^2} = P_\varepsilon\text{, wenn }k_{\rm M} = 0 \ \Rightarrow \ z(t) \equiv 0$.
(2) Variieren Sie bei sonst gleicher Einstellung wie unter (1) die Phase $\varphi_2$ im gesamten möglichen Bereich $\pm 180^\circ$. Wie ändern sich $T_0$ und $P_x$?
$\hspace{1.0cm}\Rightarrow\hspace{0.3cm}\text{Keine Veränderungen:}\hspace{0.2cm} T_0 = 2.0 \ {\rm ms}; \hspace{0.2cm} P_x = 0.5 \ {\rm V^2}$.
(3) Variieren Sie bei sonst gleicher Einstellung wie unter (1) die Frequenz $f_2$ im Bereich $0 \le f_2 \le 5\ {\rm kHz}$. Wie ändert sich die Signalleistung $P_x$?
$\hspace{1.0cm}\Rightarrow\hspace{0.3cm}\text{Keine Veränderungen, falls }f_2 \ne 0\text{ oder } f_2 \ne f_1\text{:}\hspace{0.3cm} P_x = 0.5 \ {\rm V^2}\text{.} \hspace{0.2cm} T_0 \text{ ändert sich, falls }f_2\text{ kein Vielfaches von }f_1$.
$\hspace{1.85cm}\text{Falls }f_2 = 0\text{:}\hspace{0.2cm} P_x = A_1^2/2 + A_2^2 = 0.68 \ {\rm V^2}$. $\hspace{3cm}\text{Allgemeine Formel noch überprüfen}$
$\hspace{1.85cm}\text{Falls }f_2 = f_1\text{:}\hspace{0.2cm} P_x = [A_1\cos(\varphi_1) + A_2\cos(\varphi_2)]^2/2 + [A_1\sin(\varphi_1) + A_2\sin(\varphi_2)]^2/2 \text{.}\hspace{0.2cm} \varphi_1 = 90^\circ, \ \varphi_2 = 0^\circ\text{:}\hspace{0.3cm} P_x = 0.5 \ {\rm V^2}\text{.} $
(4) Ausgehend vom bisherigen Sendesignal $x(t)$ gelte für den Kanal: $\alpha_1 = \alpha_2 = 0.5, \ \tau_1 = \tau_2 = 0.5\ {\rm ms}$. Zudem sei $k_{\rm M} = 1 \text{ und } \tau_{\rm M} = 0$ .
- Gibt es lineare Verzerrungen? Wie groß ist die Empfangsleistung $P_y$ und die Leistung $P_\varepsilon$ des Differenzsignals $\varepsilon(t) = z(t) - x(t)$?
$\hspace{1.0cm}\Rightarrow \hspace{0.3cm} y(t) = 0.5 \cdot x(t- 1\ {\rm ms})\text{ ist unverzerrt, nur gedämpft und verzögert.}$
$\hspace{1.85cm}\text{Empfangsleistung:}\hspace{0.2cm} P_y = (A_1/2)^2/2 + (A_2/2)^2/2 = 0.125 \ {\rm V^2}\text{. }\hspace{0.2cm} P_\varepsilon \text{ ist deutlich größer:} \hspace{0.2cm} P_\varepsilon = 0.625 \ {\rm V^2}.$
(5) Variieren Sie bei sonst gleicher Einstellung wie unter (4) die Matchingparameter $k_{\rm M} \text{ und } \tau_{\rm M}$. Wie groß ist die Verzerrungsleistung $P_{\rm D}$?
$\hspace{1.0cm}\Rightarrow \hspace{0.3cm} P_{\rm D}\text{ ist gleich der Leistung }P_\varepsilon \text{ des Differenzsignals bei bestmöglicher Anpassung:} \hspace{0.2cm}k_{\rm M} = 2 \text{ und } \tau_{\rm M}=T_0 - 0.5\ {\rm ms} = 1.5\ {\rm ms}$
$\hspace{1.0cm}\Rightarrow \hspace{0.3cm}z(t) = x(t)\hspace{0.3cm}\Rightarrow \hspace{0.3cm}\varepsilon(t) = 0\hspace{0.3cm}\Rightarrow \hspace{0.3cm}P_{\rm D} = P_\varepsilon = 0 \hspace{0.3cm}\Rightarrow \hspace{0.3cm}\text{weder Dämpfungs- noch Phasenverzerrungen.}$
(6) Für den Kanal gelte nun $\alpha_1 = 0.5, \hspace{0.15cm}\underline{\alpha_2 = 0.2}, \ \tau_1 = \tau_2 = 0.5\ {\rm ms}$. Wie groß sind nun die Verzerrungsleistung $P_{\rm D}$ und das $\rm SDR$ $\rho_{\rm D}$?
$\hspace{1.0cm}\Rightarrow \hspace{0.3cm} P_{\rm D} = P_\varepsilon \text{ bei bestmöglicher Anpassung:} \hspace{0.2cm}k_{\rm M}\hspace{0.15cm}\underline{ = 2.24} \text{ und } \tau_{\rm M}\hspace{0.15cm}\underline{ = 1.5\ {\rm ms} }\text{:} \hspace{0.2cm}P_{\rm D} = 0.059 \ {\rm V^2}$.
$\hspace{1.85cm}\text{Nur Dämpfungsverzerrungen.} \hspace{0.3cm}\text{Signal-zu-Verzerrung-Leistungsverhältnis}\ \rho_{\rm D} = P_x/P_\varepsilon \approx 8.5$.
(7) Für den Kanal gelte nun $\alpha_1 = \alpha_2 = 0.5, \ \tau_1 \hspace{0.15cm}\underline{= 2\ {\rm ms} }, \ \tau_2 = 0.5\ {\rm ms}$. Wie groß sind nun $P_{\rm D}$ und $\rho_{\rm D}$?
$\hspace{1.0cm}\Rightarrow \hspace{0.3cm} P_{\rm D} = P_\varepsilon \text{ bei bestmöglicher Anpassung:} \hspace{0.2cm}k_{\rm M}\hspace{0.15cm}\underline{ = 1.82} \text{ und } \tau_{\rm M}\hspace{0.15cm}\underline{ = 0.15\ {\rm ms} }\text{:} \hspace{0.2cm}P_{\rm D} = 0.072 \ {\rm V^2}$.
$\hspace{1.85cm}\text{Nur Phasenverzerrungen.} \hspace{0.3cm}\text{Signal-zu-Verzerrung-Leistungsverhältnis}\ \rho_{\rm D} = P_x/P_\varepsilon \approx 7$.
(8) Für den Kanal gelte nun $\alpha_1 = 0.5, \hspace{0.15cm}\underline{\alpha_2 = 0.2}, \ \tau_1 \hspace{0.15cm}\underline{= 2\ {\rm ms} }, \ \tau_2 = 0.5\ {\rm ms}$. Wie groß sind nun $P_{\rm D}$ und $\rho_{\rm D}$? Wie lässt sich $y(t)$ annähern?
$\hspace{1.0cm}\Rightarrow\hspace{0.3cm} \text{Dämpfungs- und Phasenverzerrungen. Bestmögliche Anpassung:} \hspace{0.2cm}k_{\rm M}\hspace{0.15cm}\underline{ = 2.06} \text{, } \tau_{\rm M}\hspace{0.15cm}\underline{ = 0.15\ {\rm ms} }\text{:} \hspace{0.2cm}P_{\rm D} = 0.136 \ {\rm V^2},\hspace{0.1cm}\rho_{\rm D} \approx 3.7$.
$\hspace{1.85cm}\text{Zusammenfassen von }\varphi \text{- und } \tau\text{-Parameter: } y(t) = 0.4 \ {\rm V} \cdot \sin\ (2\pif_1 t) - 0.12 \ {\rm V} \cdot \sin\ (2\pi \cdot 3f_1\cdot t) \approx 0.52 \ {\rm V} \cdot \sin^3(2\pi f_1 t)$.
(9) Für das Sendesignal $x(t)$ gelte nun $A_1 = A_2 = 1\ {\rm V}, \ f_1 = 1\ {\rm kHz}, \ f_2 = 1\ {\rm kHz}, \ \varphi_1 = 0^\circ, \ \varphi_2 = 0^\circ$ und der Kanal ein Tiefpass erster Ordnung $(f_0 = 2\ {\rm kHz})$. Wählen Sie die letzte Einstellung ⇒ „Recall Parameters” und ändern Sie $f_2' = 0.6$. Speichern Sie diese Einstellung mit „Store Parameters”:
$\hspace{1.0cm}\Rightarrow\hspace{0.3cm}$Die Periodendauer ist $T_0 = 5.0 \ \rm ms$ wegen ${\rm ggt}(0.2,0.6) = 0.2$.
(7) Wie groß ist bei gleicher Einstellung der maximale Signalwert $x_{\rm max}\text{?}$
$\hspace{1.0cm}\Rightarrow\hspace{0.3cm}$Der maximale Signalwert ist $x_{\rm max} =x(t_* + i \cdot T_0) = 1.39 \ \rm V$ mit $t_* = 0.3 \ \rm ms$ und $T_0 = 5.0 \ \rm ms$
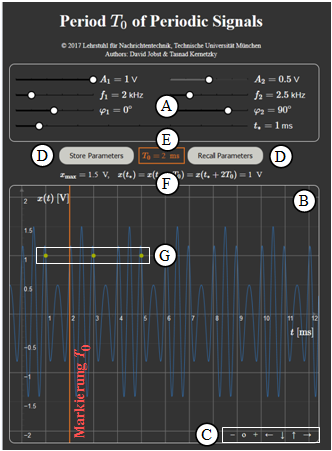
Zur Handhabung des Applets
(A) Parametereingabe per Slider
(B) Bereich der graphischen Darstellung
(C) Variationsmöglichkeit für die graphische Darstellung
(D) Abspeichern und Zurückholen von Parametersätzen
(E) Numerikausgabe des Hauptergebnisses $T_0$; graphische Verdeutlichung durch rote Linie
(F) Ausgabe von $x_{\rm max}$ und der Signalwerte $x(t_*) = x(t_* + T_0)= x(t_* + 2T_0)$
(G) Darstellung der Signalwerte $x(t_*) = x(t_* + T_0)= x(t_* + 2T_0)$ durch grüne Punkte
(H) Einstellung der Zeit $t_*$ für die Signalwerte $x(t_*) = x(t_* + T_0)= x(t_* + 2T_0)$
Details zum obigen Punkt (C)
(*) Zoom–Funktionen „$+$” (Vergrößern), „$-$” (Verkleinern) und $\rm o$ (Zurücksetzen)
(*) Verschieben mit „$\leftarrow$” (Ausschnitt nach links, Ordinate nach rechts), „$\uparrow$” „$\downarrow$” und „$\rightarrow$”
Andere Möglichkeiten:
(*) Gedrückte Shifttaste und Scrollen: Zoomen im Koordinatensystem,
(*) Gedrückte Shifttaste und linke Maustaste: Verschieben des Koordinatensystems.
Über die Autoren
Dieses interaktive Berechnungstool wurde am Lehrstuhl für Nachrichtentechnik der Technischen Universität München konzipiert und realisiert.
- Die erste Version wurde 2005 von Bettina Hirner im Rahmen ihrer Diplomarbeit mit „FlashMX–Actionscript” erstellt (Betreuer: Günter Söder ).
- 2018 wurde dieses Programm von Jimmy HeDavid Jobst im Rahmen seiner Ingenieurspraxis (Betreuer: Tasnád Kernetzky) auf „HTML5” umgesetzt und neu gestaltet ⇒ Applet-Variante 1.
- Parallel dazu erarbeitete Bastian Siebenwirth im Rahmen seiner Bachelorarbeit (Betreuer: Günter Söder) die HTML5-Variante 2.