Difference between revisions of "Applets:Lineare Verzerrungen periodischer Signale"
| Line 23: | Line 23: | ||
==Theoretischer Hintergrund== | ==Theoretischer Hintergrund== | ||
<br> | <br> | ||
| − | + | Unter '''Verzerrungen''' (englisch: ''Distortions'') versteht man allgemein die unerwünschte deterministische Veränderungen eines Nachrichtensignals durch ein Übertragungssystem. Sie sind bei vielen Nachrichtensystemen neben den stochastischen Störungen (Rauschen, Nebensprechen, etc.) eine entscheidende Begrenzung für die Übertragungsqualität und die Übertragungsrate. | |
| − | + | ||
| − | + | Ebenso wie man die „Stärke” von Rauschen durch | |
| − | * | + | *die Rauschleistung (englisch: ''Noise Power'') $P_{\rm N}$ und |
| − | * | + | *das Signal–zu–Rauschleistungsverhältnis (englisch: ''Signal–to–Noise Ratio'', SNR) $\rho_{\rm N}$ |
| − | + | ||
| − | + | ||
| − | + | bewertet, verwendet man zur Quantifizierung der Verzerrungen | |
| + | |||
| + | *die Verzerrungsleistung (englisch: ''Distortion Power'') $P_{\rm D}$ und | ||
| + | *das Signal–zu–Verzerrungsleistungsverhältnis (englisch: ''Signal–to–Distortion Ratio'', SDR) | ||
| + | :$$\rho_{\rm D}=\frac{\rm Signalleistung}{\rm Verzerrungsleistung} = \frac{P_x}{P_{\rm D} }.$$ | ||
| + | |||
| + | |||
| + | === Lineare und nichtlineare Verzerrungen === | ||
| + | <br> | ||
| + | Man unterscheidet zwischen linearen und nichtlinearen Verzerrungen: | ||
| + | *'''Nichtlineare Verzerrungen''' gibt es, wenn zu allen Zeiten $t$ zwischen dem Signalwert $x = x(t)$ am Eingang und dem Ausgangssignalwert $y = y(t)$ der nichtlineare Zusammenhang $y = g(x) \ne {\rm const.} \cdot x$ besteht, wobei $y = g(x)$ als die nichtlineare Kennlinie des Systems bezeichnet. Legt man an den Eingang ein Cosinussignal der Freuenz $f_0$ an, so beinhaltet das Ausgangssignalwert neben $f_0$ auch Vielfach hiervon ⇒ Oberwellen. Durch nichtlineare Verzerrungen entstehen also neue Frequenzen. | ||
| + | |||
| + | [[File:LZI_T_2_2_S3_vers2.png|center|frame|Zur Verdeutlichung nichtlinearer Verzerrungen |class=fit]] | ||
| + | |||
| + | [[File:P_ID899__LZI_T_2_3_S1_neu.png|right |frame| Beschreibung eines linearen Systems|class=fit]] | ||
| + | *'''Lineare Verzerrungen''' entstehen dann, wenn der Übertragungskanal durch einen Frequenzgang $H(f) \ne \rm const.$ charakterisiert wird. Dann werden unterschiedliche Frequenzen unterschiedlich gedämpft und unterschiedlich verzögert. Charakteristisch hierfür ist, dass zwar Frequenzen verschwinden können (zum Beispiel durch einen Tiefpass oder einen Hochpass), dass aber keine neuen Frequenzen entstehen. | ||
| + | In diesem Applet werden nur lineare Verzerrungen betrachtet. | ||
| − | |||
| − | |||
| − | :$$ | + | === Beschreibungsformen für den Frequenzgang === |
| − | + | <br> | |
| + | Der im Allgemeinen komplexe Frequenzgang kann auch wie folgt dargestellt werden: | ||
| + | :$$H(f) = |H(f)| \cdot {\rm e}^{-{\rm j} \hspace{0.05cm} \cdot | ||
| + | \hspace{0.05cm} b(f)} = {\rm e}^{-a(f)}\cdot {\rm e}^{-{\rm j} | ||
| + | \hspace{0.05cm} \cdot \hspace{0.05cm} b(f)}.$$ | ||
| + | Daraus ergeben sich folgende Beschreibungsgrößen: | ||
| + | *Der Betrag $|H(f)|$ wird als '''Amplitudengang''' und in logarithmierter Form als '''Dämpfungsverlauf''' bezeichnet: | ||
| + | :$$a(f) = - \ln |H(f)|\hspace{0.2cm}{\rm in \hspace{0.1cm}Neper | ||
| + | \hspace{0.1cm}(Np) } = - 20 \cdot \lg |H(f)|\hspace{0.2cm}{\rm in | ||
| + | \hspace{0.1cm}Dezibel \hspace{0.1cm}(dB) }.$$ | ||
| + | *Der '''Phasengang''' $b(f)$ gibt den negativen frequenzabhängigen Winkel von $H(f)$ in der komplexen Ebene an, bezogen auf die reelle Achse: | ||
| + | :$$b(f) = - {\rm arc} \hspace{0.1cm}H(f) \hspace{0.2cm}{\rm in | ||
| + | \hspace{0.1cm}Radian \hspace{0.1cm}(rad)}.$$ | ||
| − | + | === Tiefpass <i>N</i>–Ordnung === | |
| − | $\ | + | <br> |
| + | Der Frequenzgang eines realisierbaren Tiefpasses <i>N</i>–Ordnung lautet: | ||
| + | :$$H(f) = \left [\frac{1}{1 + {\rm j}\cdot f/f_0 }\right ]^N\hspace{0.05cm}.$$ | ||
| + | Ein einfacher RC–Tiefpass hat diesen Verlauf mit $N=1$. Damit erhält man | ||
| + | *den Dämpfungsverlauf: | ||
| + | :$$a(f) =N/2 \cdot \ln [1+( f/f_0)^2] \hspace{0.05cm},$$ | ||
| + | *den Phasenverlauf: | ||
| + | :$$b(f) =N \cdot \arctan( f/f_0) \hspace{0.05cm},$$ | ||
| + | *den Dämpfungsfaktor für die Frequenz $f=f_i$: | ||
| + | :$$\alpha_i =|H(f = f_i)| = [1+( f/f_0)^2]^{N/2} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} x(t)= A_i\cdot \cos(2\pi f_i t) \hspace{0.1cm}\rightarrow \hspace{0.1cm} y(t)= \alpha_i \cdot A_i\cdot \cos(2\pi f_i t)\hspace{0.05cm},$$ | ||
| + | *die Phasenlaufzeit für die Frequenz $f=f_i$: | ||
| + | :$$\tau_i =\frac{b(f_i)}{2 \pi f_i} = \frac{N \cdot \arctan( f_i/f_0)}{2 \pi f_i} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} x(t)= A_i\cdot \cos(2\pi f_i t) \hspace{0.1cm}\rightarrow \hspace{0.1cm} y(t)=A_i\cdot \cos(2\pi f_i (t- \tau_i))\hspace{0.05cm},$$ | ||
| − | + | [[File:Tiefpass.png|center|frame|Dämpfungsverlauf und Phasenverlauf eines Tiefpasses <i>N</i>–Ordnung]] | |
| − | + | === Hochpass <i>N</i>–Ordnung === | |
| + | <br> | ||
| + | Der Frequenzgang eines realisierbaren Hochpasses <i>N</i>–Ordnung lautet: | ||
| + | :$$H(f) = \left [\frac{ {\rm j}\cdot f/f_0 }{1 + {\rm j}\cdot f/f_0 }\right ]^N\hspace{0.05cm}.$$ | ||
| + | Ein einfacher LC–Tiefpass hat diesen Verlauf mit $N=1$. Damit erhält man | ||
| + | *den Dämpfungsverlauf: | ||
| + | :$$a(f) =N/2 \cdot \ln [1+( f_0/f)^2] \hspace{0.05cm},$$ | ||
| + | *den Phasenverlauf: | ||
| + | :$$b(f) =-N \cdot \arctan( f_0/f) \hspace{0.05cm},$$ | ||
| + | *den Dämpfungsfaktor für die Frequenz $f=f_i$: | ||
| + | :$$\alpha_i =|H(f = f_i)| = [1+( f_0/f)^2]^{N/2} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} x(t)= A_i\cdot \cos(2\pi f_i t) \hspace{0.1cm}\rightarrow \hspace{0.1cm} y(t)= \alpha_i \cdot A_i\cdot \cos(2\pi f_i t)\hspace{0.05cm},$$ | ||
| + | *die Phasenlaufzeit für die Frequenz $f=f_i$: | ||
| + | :$$\tau_i =\frac{b(f_i)}{2\pif_i} = \frac{-N \cdot \arctan( f_0/f_i)}{2\pif_i} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} x(t)= A_i\cdot \cos(2\pi f_i t) \hspace{0.1cm}\rightarrow \hspace{0.1cm} y(t)=A_i\cdot \cos(2\pi f_i (t- \tau_i))\hspace{0.05cm},$$ | ||
| + | [[File:Hochpass.png|center|frame|Dämpfungsverlauf und Phasenverlauf eines Hochpasses <i>N</i>–Ordnung]] | ||
| − | + | === Laufzeiten bei Tiefpass und Hochpass === | |
| − | |||
| − | + | === Dämpfungsverzerrungen und Phasenverzerrungen === | |
| − | $\ | + | Lineare Verzerrungen treten üblicherweise in Form von |
| + | * Dämpfungsverzerrungen $\alpha_i$ und | ||
| + | * Phasenverzerrungen $\tau_i$ auf. | ||
| + | Ist $\alpha_1 \ne \alpha_2$ und $\tau_1 = \tau_2$, so liegen ausschließlich Dämpfungsverzerrungen vor. | ||
| + | Dagegen führt $\alpha_1 = \alpha_2$ und $\tau_1 \ne \tau_2$ zu reinen Phasenverzerrungen.<br /> | ||
| + | Ein Signal $y(t)$ ist gegenüber $x(t)$ unverzerrt, wenn $\alpha_1 = \alpha_2$ und $\tau_1 und \tau_2$ gilt. | ||
| − | |||
| − | |||
| − | |||
==Vorschlag für die Versuchsdurchführung== | ==Vorschlag für die Versuchsdurchführung== | ||
Revision as of 17:31, 12 January 2018
Contents
Programmbeschreibung
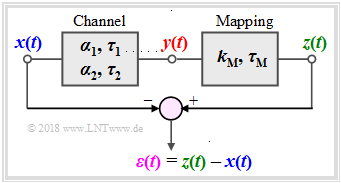
Dieses Applet veranschaulicht die Auswirkungen von linearen Verzerrungen (Dämpfungsverzerrungen und Phasenverzerrungen) anhand
- des Eingangssignals $x(t)$ ⇒ Leistung $P_x$:
- $$x(t) = x_1(t) + x_2(t) = A_1\cdot \cos\left(2\pi f_1\cdot t- \varphi_1\right)+A_2\cdot \cos\left(2\pi f_2\cdot t- \varphi_2\right), $$
- des Ausgangssignals $y(t)$ ⇒ Leistung $P_y$:
- $$y(t) = \alpha_1 \cdot x_1(t-\tau_1) + \alpha_2 \cdot x_2(t-\tau_2),$$
- des Matching–Ausgangssignals $z(t)$ ⇒ Leistung $P_z$:
- $$z(t) = k_{\rm M} \cdot y(t-\tau_{\rm M}) + \alpha_2 \cdot x_2(t-\tau_2),$$
- des Differenzsignals $\varepsilon(t) = z(t) - x(t)$ ⇒ Leistung $P_\varepsilon$.
Die Amplituden– und Phasenanpassung des Ausgangssignals $y(t)$ ⇒ „Matching” erlaubt die Unterscheidung
- zwischen einer Dämpfungsverzerrung und einer frequenzunabhängigen Dämpfung, sowie
- zwischen einer Phasenverzerrung und einer reinen Laufzeit.
Als Maß für die Stärke der linearen Verzerrungen wird die Verzerrungsleistung (englisch: Distortion Power) $P_{\rm D}$ ausgegeben.
Theoretischer Hintergrund
Unter Verzerrungen (englisch: Distortions) versteht man allgemein die unerwünschte deterministische Veränderungen eines Nachrichtensignals durch ein Übertragungssystem. Sie sind bei vielen Nachrichtensystemen neben den stochastischen Störungen (Rauschen, Nebensprechen, etc.) eine entscheidende Begrenzung für die Übertragungsqualität und die Übertragungsrate.
Ebenso wie man die „Stärke” von Rauschen durch
- die Rauschleistung (englisch: Noise Power) $P_{\rm N}$ und
- das Signal–zu–Rauschleistungsverhältnis (englisch: Signal–to–Noise Ratio, SNR) $\rho_{\rm N}$
bewertet, verwendet man zur Quantifizierung der Verzerrungen
- die Verzerrungsleistung (englisch: Distortion Power) $P_{\rm D}$ und
- das Signal–zu–Verzerrungsleistungsverhältnis (englisch: Signal–to–Distortion Ratio, SDR)
- $$\rho_{\rm D}=\frac{\rm Signalleistung}{\rm Verzerrungsleistung} = \frac{P_x}{P_{\rm D} }.$$
Lineare und nichtlineare Verzerrungen
Man unterscheidet zwischen linearen und nichtlinearen Verzerrungen:
- Nichtlineare Verzerrungen gibt es, wenn zu allen Zeiten $t$ zwischen dem Signalwert $x = x(t)$ am Eingang und dem Ausgangssignalwert $y = y(t)$ der nichtlineare Zusammenhang $y = g(x) \ne {\rm const.} \cdot x$ besteht, wobei $y = g(x)$ als die nichtlineare Kennlinie des Systems bezeichnet. Legt man an den Eingang ein Cosinussignal der Freuenz $f_0$ an, so beinhaltet das Ausgangssignalwert neben $f_0$ auch Vielfach hiervon ⇒ Oberwellen. Durch nichtlineare Verzerrungen entstehen also neue Frequenzen.
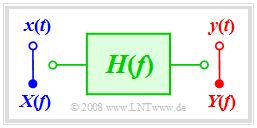
- Lineare Verzerrungen entstehen dann, wenn der Übertragungskanal durch einen Frequenzgang $H(f) \ne \rm const.$ charakterisiert wird. Dann werden unterschiedliche Frequenzen unterschiedlich gedämpft und unterschiedlich verzögert. Charakteristisch hierfür ist, dass zwar Frequenzen verschwinden können (zum Beispiel durch einen Tiefpass oder einen Hochpass), dass aber keine neuen Frequenzen entstehen.
In diesem Applet werden nur lineare Verzerrungen betrachtet.
Beschreibungsformen für den Frequenzgang
Der im Allgemeinen komplexe Frequenzgang kann auch wie folgt dargestellt werden:
- $$H(f) = |H(f)| \cdot {\rm e}^{-{\rm j} \hspace{0.05cm} \cdot \hspace{0.05cm} b(f)} = {\rm e}^{-a(f)}\cdot {\rm e}^{-{\rm j} \hspace{0.05cm} \cdot \hspace{0.05cm} b(f)}.$$
Daraus ergeben sich folgende Beschreibungsgrößen:
- Der Betrag $|H(f)|$ wird als Amplitudengang und in logarithmierter Form als Dämpfungsverlauf bezeichnet:
- $$a(f) = - \ln |H(f)|\hspace{0.2cm}{\rm in \hspace{0.1cm}Neper \hspace{0.1cm}(Np) } = - 20 \cdot \lg |H(f)|\hspace{0.2cm}{\rm in \hspace{0.1cm}Dezibel \hspace{0.1cm}(dB) }.$$
- Der Phasengang $b(f)$ gibt den negativen frequenzabhängigen Winkel von $H(f)$ in der komplexen Ebene an, bezogen auf die reelle Achse:
- $$b(f) = - {\rm arc} \hspace{0.1cm}H(f) \hspace{0.2cm}{\rm in \hspace{0.1cm}Radian \hspace{0.1cm}(rad)}.$$
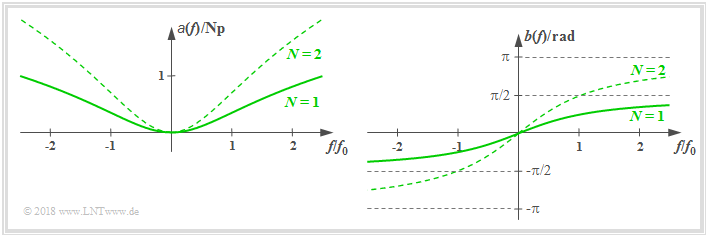
Tiefpass N–Ordnung
Der Frequenzgang eines realisierbaren Tiefpasses N–Ordnung lautet:
- $$H(f) = \left [\frac{1}{1 + {\rm j}\cdot f/f_0 }\right ]^N\hspace{0.05cm}.$$
Ein einfacher RC–Tiefpass hat diesen Verlauf mit $N=1$. Damit erhält man
- den Dämpfungsverlauf:
- $$a(f) =N/2 \cdot \ln [1+( f/f_0)^2] \hspace{0.05cm},$$
- den Phasenverlauf:
- $$b(f) =N \cdot \arctan( f/f_0) \hspace{0.05cm},$$
- den Dämpfungsfaktor für die Frequenz $f=f_i$:
- $$\alpha_i =|H(f = f_i)| = [1+( f/f_0)^2]^{N/2} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} x(t)= A_i\cdot \cos(2\pi f_i t) \hspace{0.1cm}\rightarrow \hspace{0.1cm} y(t)= \alpha_i \cdot A_i\cdot \cos(2\pi f_i t)\hspace{0.05cm},$$
- die Phasenlaufzeit für die Frequenz $f=f_i$:
- $$\tau_i =\frac{b(f_i)}{2 \pi f_i} = \frac{N \cdot \arctan( f_i/f_0)}{2 \pi f_i} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} x(t)= A_i\cdot \cos(2\pi f_i t) \hspace{0.1cm}\rightarrow \hspace{0.1cm} y(t)=A_i\cdot \cos(2\pi f_i (t- \tau_i))\hspace{0.05cm},$$
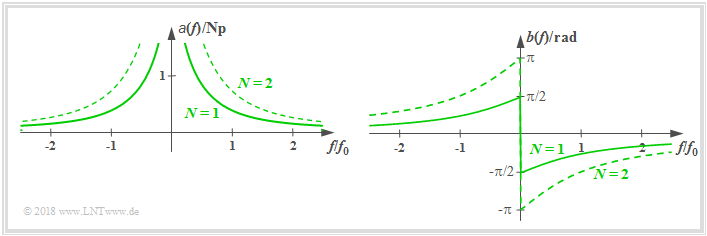
Hochpass N–Ordnung
Der Frequenzgang eines realisierbaren Hochpasses N–Ordnung lautet:
- $$H(f) = \left [\frac{ {\rm j}\cdot f/f_0 }{1 + {\rm j}\cdot f/f_0 }\right ]^N\hspace{0.05cm}.$$
Ein einfacher LC–Tiefpass hat diesen Verlauf mit $N=1$. Damit erhält man
- den Dämpfungsverlauf:
- $$a(f) =N/2 \cdot \ln [1+( f_0/f)^2] \hspace{0.05cm},$$
- den Phasenverlauf:
- $$b(f) =-N \cdot \arctan( f_0/f) \hspace{0.05cm},$$
- den Dämpfungsfaktor für die Frequenz $f=f_i$:
- $$\alpha_i =|H(f = f_i)| = [1+( f_0/f)^2]^{N/2} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} x(t)= A_i\cdot \cos(2\pi f_i t) \hspace{0.1cm}\rightarrow \hspace{0.1cm} y(t)= \alpha_i \cdot A_i\cdot \cos(2\pi f_i t)\hspace{0.05cm},$$
- die Phasenlaufzeit für die Frequenz $f=f_i$:
- $$\tau_i =\frac{b(f_i)}{2\pif_i} = \frac{-N \cdot \arctan( f_0/f_i)}{2\pif_i} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} x(t)= A_i\cdot \cos(2\pi f_i t) \hspace{0.1cm}\rightarrow \hspace{0.1cm} y(t)=A_i\cdot \cos(2\pi f_i (t- \tau_i))\hspace{0.05cm},$$
Laufzeiten bei Tiefpass und Hochpass
Dämpfungsverzerrungen und Phasenverzerrungen
Lineare Verzerrungen treten üblicherweise in Form von
- Dämpfungsverzerrungen $\alpha_i$ und
- Phasenverzerrungen $\tau_i$ auf.
Ist $\alpha_1 \ne \alpha_2$ und $\tau_1 = \tau_2$, so liegen ausschließlich Dämpfungsverzerrungen vor.
Dagegen führt $\alpha_1 = \alpha_2$ und $\tau_1 \ne \tau_2$ zu reinen Phasenverzerrungen.
Ein Signal $y(t)$ ist gegenüber $x(t)$ unverzerrt, wenn $\alpha_1 = \alpha_2$ und $\tau_1 und \tau_2$ gilt.
Vorschlag für die Versuchsdurchführung
BlaBla
(1) Für das Sendesignal $x(t)$ gelte $A_1 = 0.8\ {\rm V}, \ A_2 = 0.6\ {\rm V}, \ f_1 = 0.5\ {\rm kHz}, \ f_2 = 1.5\ {\rm kHz}, \ \varphi_1 = 90^\circ, \ \varphi_2 = 0^\circ$.
- Wie groß ist die Periodendauer $T_0$? Welche Leistung $P_x$ weist dieses Signal auf? Wo können Sie diesen Wert im Programm ablesen?
$\hspace{1.0cm}\Rightarrow\hspace{0.3cm}T_0 = \big [\hspace{-0.1cm}\text{ größter gemeinsamer Teiler }(0.5 \ {\rm kHz}, \ 1.5 \ {\rm kHz})\big ]^{-1}\hspace{0.15cm}\underline{ = 2.0 \ {\rm ms}};$
$\hspace{1.85cm} P_x = A_1^2/2 + A_2^2/2 \hspace{0.15cm}\underline{= 0.5 \ {\rm V^2}} = P_\varepsilon\text{, wenn }\hspace{0.15cm}\underline{k_{\rm M} = 0} \ \Rightarrow \ z(t) \equiv 0$.
(2) Variieren Sie bei sonst gleicher Einstellung wie unter (1) die Phase $\varphi_2$ im gesamten möglichen Bereich $\pm 180^\circ$. Wie ändern sich $T_0$ und $P_x$?
$\hspace{1.0cm}\Rightarrow\hspace{0.3cm}\text{Keine Veränderungen:}\hspace{0.2cm}\hspace{0.15cm}\underline{ T_0 = 2.0 \ {\rm ms}; \hspace{0.2cm} P_x = 0.5 \ {\rm V^2}}$.
(3) Variieren Sie bei sonst gleicher Einstellung wie unter (1) die Frequenz $f_2$ im Bereich $0 \le f_2 \le 5\ {\rm kHz}$. Wie ändert sich die Signalleistung $P_x$?
$\hspace{1.0cm}\Rightarrow\hspace{0.3cm}\text{Keine Veränderungen, falls }f_2 \ne 0\text{ oder } f_2 \ne f_1\text{:}\hspace{0.3cm} \hspace{0.15cm}\underline{P_x = 0.5 \ {\rm V^2}}\text{.} \hspace{0.2cm} T_0 \text{ ändert sich, falls }f_2\text{ kein Vielfaches von }f_1$.
$\hspace{1.85cm}\text{Falls }f_2 = 0\text{:}\hspace{0.2cm} P_x = A_1^2/2 + A_2^2\hspace{0.15cm}\underline{ = 0.68 \ {\rm V^2}}$. $\hspace{3cm}\text{Allgemeine Formel noch überprüfen}$
$\hspace{1.85cm}\text{Falls }f_2 = f_1\text{:}\hspace{0.2cm} P_x = [A_1\cos(\varphi_1) + A_2\cos(\varphi_2)]^2/2 + [A_1\sin(\varphi_1) + A_2\sin(\varphi_2)]^2/2 \text{. Mit } \varphi_1 = 90^\circ, \ \varphi_2 = 0^\circ\text{:}\hspace{0.3cm}\hspace{0.15cm}\underline{ P_x = 0.5 \ {\rm V^2}}\text{.} $
(4) Ausgehend vom bisherigen Sendesignal $x(t)$ gelte für den Kanal: $\alpha_1 = \alpha_2 = 0.5, \ \tau_1 = \tau_2 = 0.5\ {\rm ms}$. Zudem sei $k_{\rm M} = 1 \text{ und } \tau_{\rm M} = 0$ .
- Gibt es lineare Verzerrungen? Wie groß ist die Empfangsleistung $P_y$ und die Leistung $P_\varepsilon$ des Differenzsignals $\varepsilon(t) = z(t) - x(t)$?
$\hspace{1.0cm}\Rightarrow \hspace{0.3cm}\hspace{0.15cm}\underline{ y(t) = 0.5 \cdot x(t- 1\ {\rm ms})}\text{ ist unverzerrt, nur gedämpft und verzögert.}$
$\hspace{1.85cm}\text{Empfangsleistung:}\hspace{0.2cm} P_y = (A_1/2)^2/2 + (A_2/2)^2/2\hspace{0.15cm}\underline{ = 0.125 \ {\rm V^2}}\text{. } P_\varepsilon \text{ ist deutlich größer:} \hspace{0.1cm} \hspace{0.15cm}\underline{P_\varepsilon = 0.625 \ {\rm V^2}}.$
(5) Variieren Sie bei sonst gleicher Einstellung wie unter (4) die Matchingparameter $k_{\rm M} \text{ und } \tau_{\rm M}$. Wie groß ist die Verzerrungsleistung $P_{\rm D}$?
$\hspace{1.0cm}\Rightarrow \hspace{0.3cm} P_{\rm D}\text{ ist gleich der Leistung }P_\varepsilon \text{ des Differenzsignals bei bestmöglicher Anpassung:} \hspace{0.2cm}k_{\rm M} = 2 \text{ und } \tau_{\rm M}=T_0 - 0.5\ {\rm ms} = 1.5\ {\rm ms}$
$\hspace{1.0cm}\Rightarrow \hspace{0.3cm}z(t) = x(t)\hspace{0.3cm}\Rightarrow \hspace{0.3cm}\varepsilon(t) = 0\hspace{0.3cm}\Rightarrow \hspace{0.3cm}P_{\rm D}\hspace{0.15cm}\underline{ = P_\varepsilon = 0} \hspace{0.3cm}\Rightarrow \hspace{0.3cm}\text{weder Dämpfungs- noch Phasenverzerrungen.}$
(6) Für den Kanal gelte nun $\alpha_1 = 0.5, \hspace{0.15cm}\underline{\alpha_2 = 0.2}, \ \tau_1 = \tau_2 = 0.5\ {\rm ms}$. Wie groß sind nun die Verzerrungsleistung $P_{\rm D}$ und das $\rm SDR$ $\rho_{\rm D}$?
$\hspace{1.0cm}\Rightarrow \hspace{0.3cm} P_{\rm D} = P_\varepsilon \text{ bei bestmöglicher Anpassung:} \hspace{0.2cm}\hspace{0.15cm}\underline{k_{\rm M} = 2.24} \text{ und } \hspace{0.15cm}\underline{\tau_{\rm M} = 1.5\ {\rm ms} }\text{:} \hspace{0.2cm}\hspace{0.15cm}\underline{P_{\rm D} = 0.059 \ {\rm V^2}}$.
$\hspace{1.85cm}\text{Nur Dämpfungsverzerrungen.} \hspace{0.3cm}\text{Signal-zu-Verzerrung-Leistungsverhältnis}\ \hspace{0.15cm}\underline{\rho_{\rm D} = P_x/P_\varepsilon \approx 8.5}$.
(7) Für den Kanal gelte nun $\alpha_1 = \alpha_2 = 0.5, \ \tau_1 \hspace{0.15cm}\underline{= 2\ {\rm ms} }, \ \tau_2 = 0.5\ {\rm ms}$. Wie groß sind nun $P_{\rm D}$ und $\rho_{\rm D}$?
$\hspace{1.0cm}\Rightarrow \hspace{0.3cm} P_{\rm D} = P_\varepsilon \text{ bei bestmöglicher Anpassung:} \hspace{0.2cm}\hspace{0.15cm}\underline{k_{\rm M} = 1.82} \text{ und } \tau_{\rm M}\hspace{0.15cm}\underline{ = 0.15\ {\rm ms} }\text{:} \hspace{0.2cm}\hspace{0.15cm}\underline{P_{\rm D} = 0.072 \ {\rm V^2}}$.
$\hspace{1.85cm}\text{Nur Phasenverzerrungen.} \hspace{0.3cm}\text{Signal-zu-Verzerrung-Leistungsverhältnis}\ \hspace{0.15cm}\underline{\rho_{\rm D} = P_x/P_\varepsilon \approx 7}$.
(8) Für den Kanal gelte nun $\hspace{0.15cm}\underline{\alpha_1 = 0.5} , \hspace{0.15cm}\underline{\alpha_2 = 0.2} , \ \hspace{0.15cm}\underline{\tau_1= 2\ {\rm ms} }, \ \hspace{0.15cm}\underline{\tau_2 = 0.5\ {\rm ms} }$. Wie groß sind nun $P_{\rm D}$ und $\rho_{\rm D}$? Wie lässt sich $y(t)$ annähern?
$\hspace{1.0cm}\Rightarrow\hspace{0.3cm} \text{Dämpfungs- und Phasenverzerrungen. Bestmögliche Anpassung:} \hspace{0.2cm}\hspace{0.15cm}\underline{k_{\rm M} = 2.06} \text{, } \hspace{0.15cm}\underline{\tau_{\rm M} = 0.15\ {\rm ms} }\text{:} \hspace{0.2cm}\hspace{0.15cm}\underline{P_{\rm D} = 0.136 \ {\rm V^2}},\hspace{0.1cm}\hspace{0.15cm}\underline{\rho_{\rm D} \approx 3.7}$.
$\hspace{1.85cm}\text{Zusammenfassen von }\varphi \text{- und } \tau\text{-Parameter: } y(t) = 0.4 \ {\rm V} \cdot \sin\ (2\pi f_1 t) - 0.12 \ {\rm V} \cdot \sin\ (2\pi \cdot 3f_1\cdot t) \hspace{0.15cm}\underline{\approx 0.52 \ {\rm V} \cdot \sin^3(2\pi f_1 t)}$.
(9) Nun gelte $\underline{A_1 = A_2 = 1\ {\rm V}, \ f_1 = 1\ {\rm kHz}, \ f_2 = 1\ {\rm kHz}, \ \varphi_1 = 0^\circ, \ \varphi_2 = 0^\circ}$. Der Kanal sei ein Tiefpass erster Ordnung $\underline{(f_0 = 1\ {\rm kHz})}$.
- Gibt es Dämpfungsverzerrungen? Gibt es Phasenverzerrungen? Wie groß ist nun die Verzerrungsleistung $P_{\rm D}$?
$\hspace{1.0cm}\Rightarrow\hspace{0.3cm} \text{Dämpfungsverzerrungen, da }\hspace{0.15cm}\underline{\alpha_1 = 0.71 \ne \alpha_2 = 0.45} \text{; geringere Phasenverzerrungen, da }\hspace{0.15cm}\underline{ \tau_1 = 0.13 \ {\rm ms} \approx \tau_2 = 0.09 \ {\rm ms}}$.
$\hspace{1.85cm}\text{ Verzerrungsleistung }\hspace{0.15cm}\underline{P_{\rm D} = 0.074 \ {\rm V^2}} \text{ bei bestmöglicher Anpassung:} \hspace{0.2cm}k_{\rm M}\hspace{0.15cm}\underline{ = 1.6} \text{ und } \tau_{\rm M}\hspace{0.15cm}\underline{ = 0.9\ {\rm ms} }$.
(10) Wie ändern sich die Kanalparameter durch einen Tiefpass zweiter Ordnung gegenüber einem Tiefpass erster Ordnung $(f_0 = 1\ {\rm kHz})$.
- Wie groß ist nun die Verzerrungsleistung $P_{\rm D}$? Wie groß ist nun die Verzerrungsleistung $P_{\rm D}$?
$\hspace{1.0cm}\Rightarrow\hspace{0.3cm} \text{Es gilt }\hspace{0.15cm}\underline{\alpha_1 = 0.71^2 \approx 0.5, \alpha_2 = 0.45^2 \approx 0.5, \tau_1 = 2 \cdot 0.13 \approx 0.25 \ {\rm ms} \tau_2 = 2 \cdot 0.09 \ {\rm ms} \approx 0.18 \ {\rm ms}} $.
$\hspace{1.85cm}P_{\rm D} = 0.228 \ {\rm V^2} \text { ist größer und der 2 kHz-Anteil wird im Vergleich zum 2 kHz-Anteil noch mehr unterdrückt}$.
(11) Welche Unterschiede ergeben sich bei einem Hochpass zweiter Ordnung gegenüber einem Tiefpass zweiter Ordnung $(f_0 = 1\ {\rm kHz})$.
$\hspace{1.0cm}\Rightarrow\hspace{0.3cm} \text{???????????????}$
Zur Handhabung des Applets
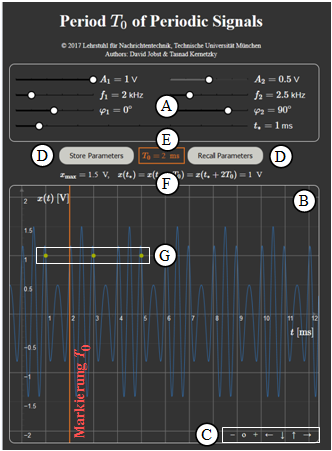
(A) Parametereingabe per Slider
(B) Bereich der graphischen Darstellung
(C) Variationsmöglichkeit für die graphische Darstellung
(D) Abspeichern und Zurückholen von Parametersätzen
(E) Numerikausgabe des Hauptergebnisses $T_0$; graphische Verdeutlichung durch rote Linie
(F) Ausgabe von $x_{\rm max}$ und der Signalwerte $x(t_*) = x(t_* + T_0)= x(t_* + 2T_0)$
(G) Darstellung der Signalwerte $x(t_*) = x(t_* + T_0)= x(t_* + 2T_0)$ durch grüne Punkte
(H) Einstellung der Zeit $t_*$ für die Signalwerte $x(t_*) = x(t_* + T_0)= x(t_* + 2T_0)$
Details zum obigen Punkt (C)
(*) Zoom–Funktionen „$+$” (Vergrößern), „$-$” (Verkleinern) und $\rm o$ (Zurücksetzen)
(*) Verschieben mit „$\leftarrow$” (Ausschnitt nach links, Ordinate nach rechts), „$\uparrow$” „$\downarrow$” und „$\rightarrow$”
Andere Möglichkeiten:
(*) Gedrückte Shifttaste und Scrollen: Zoomen im Koordinatensystem,
(*) Gedrückte Shifttaste und linke Maustaste: Verschieben des Koordinatensystems.
Über die Autoren
Dieses interaktive Berechnungstool wurde am Lehrstuhl für Nachrichtentechnik der Technischen Universität München konzipiert und realisiert.
- Die erste Version wurde 2005 von Bettina Hirner im Rahmen ihrer Diplomarbeit mit „FlashMX–Actionscript” erstellt (Betreuer: Günter Söder ).
- 2018 wurde dieses Programm von Jimmy He im Rahmen seiner Bachelorarbeit (Betreuer: Tasnád Kernetzky) auf „HTML5” umgesetzt und neu gestaltet.