Aufgaben:Exercise 3.09: Basics of the Viterbi Algorithm

• Return to book

Zu analysierendes Trellis

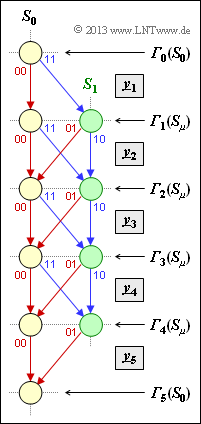
Die Grafik zeigt ein Trellisdiagramm und definiert gleichzeitig die Fehlergrößen ${\it \Gamma}_i(S_0)$ und ${\it \Gamma}_i(S_1)$ zu den Zeitpunkten $i = 0$ bis $i = 5$. Aus diesem Trellis können zum Beispiel abgelesen werden:

• die Coderate $R$,
• das Gedächtnis $m$,
• die freie Distanz $d_{\rm F}$,
• die Informationssequenzlänge $L$,
• die Sequenzlänge $L'$ inklusive der Terminierung.

In der Aufgabe ist weiter zu klären:

• die Bedeutung des Endwertes ${\it \Gamma}_5(S_0)$,
• Auswirkungen von einem bzw. zwei Übertragungsfehlern.

Hinweise:

• Die Aufgabe gehört zum Kapitel Decodierung von Faltungscodes.
• Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.

Fragebogen

1

Welche der folgenden Aussagen werden durch das Trellis bestätigt?

	Es handelt sich um einen Rate–1/2–Faltungscode.
	Das Gedächtnis des Codes ist $m = 2$.
	Der Faltungscode ist terminiert.
	Die Länge der Informationssequenz ist $L = 5$.

2

Geben Sie die freie Distanz $d_{\rm F}$ des Faltungscodes an.

$d_{\rm F} \ = \ $

3

Welche Aussagen erlaubt der Endwert ${\it \Gamma}_5(S_0) = 0$ der Fehlergröße?

	Es ist kein Übertragungsfehler aufgetreten.
	Das Decodierergebnis $\underline{v}$ ist mit Sicherheit richtig (gleich $\underline{u}$).
	Das Decodierergebnis minimiert die Wahrscheinlichkeit ${\rm Pr}(\underline{v} ≠ \underline{u}$).

4

Welche Aussagen treffen bei einem einzigen Übertragungsfehler zu?

	Der Fehlergrößenendwert ist ${\it \Gamma}_5(S_0) = 1$.
	Das Decodierergebnis $\underline{v}$ ist mit Sicherheit richtig (gleich $\underline{u}$).
	Das Decodierergebnis minimiert die Wahrscheinlichkeit ${\rm Pr}(\underline{v} ≠ \underline{u}$).

5

Welche Aussagen treffen bei zwei Übertragungsfehlern zu?

	Der Fehlergrößenendwert ist ${\it \Gamma}_5(S_0) = 2$.
	Das Decodierergebnis $\underline{v}$ ist mit Sicherheit richtig (gleich $\underline{u}$).
	Das Decodierergebnis $\underline{v}$ ist mit Sicherheit falsch (ungleich $\underline{u}$).

Musterlösung

Solution

(1)  Richtig sind die Lösungsvorschläge 1 und 3. Es gibt hier $2^{k \cdot m} = 2$ Zustände. Daraus folgt $k = 1$ und $m = 1$. Pro Codierschritt werden $n = 2$ Codebits ausgegeben  ⇒  $R = 1/2$. Die Informationssequenzlänge ist $L = 4$. Erst durch ein (da $m = 1$) zusätzliches Terminierungsbit kommt man zur Gesamtlänge $L' = 5$.

(2)  Die freie Distanz $d_{\rm F}$ ist definiert als die Anzahl der Codebits, in denen sich zwei Sequenzen $\underline{x}$ und $\underline{x'}$ unterscheiden. Als Bezugssequenz wählen wir die Nullsequenz:

$$\underline{x}\hspace{0.03cm}' = \underline{0} = \big (00\hspace{0.05cm}, 00\hspace{0.05cm}, 00\hspace{0.05cm}, 00\hspace{0.05cm}, ... \hspace{0.1cm} \big ) \hspace{0.05cm},$$

ausgedrückt mit der Zustandsabfolge:   $S_0 → S_0 → S_0 → S_0 → \ ... \ $ Eine der Folgen $\underline{x} ≠ \underline{0}$, die sich von $\underline{0}$ nur in der minimalen Anzahl an Codebits unterscheidet, folgt dem Pfad $S_0 → S_1 → S_0 → S_0 → \ ... \ $ :

$$\underline{x} = \big (11\hspace{0.05cm}, 01\hspace{0.05cm}, 00\hspace{0.05cm}, 00\hspace{0.05cm}, ... \hspace{0.1cm} \big ) \hspace{0.3cm}\Rightarrow \hspace{0.3cm} d_{\rm F}\hspace{0.1cm}\underline{ = 3} \hspace{0.05cm}.$$

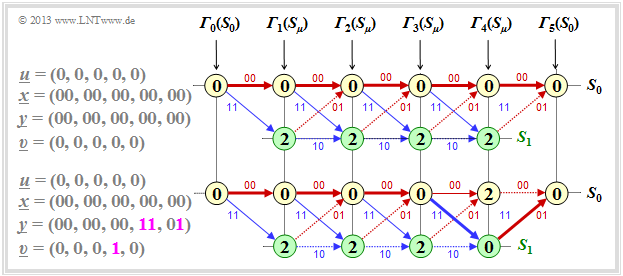
(3)  Wird die Nullsequenz gesendet und diese auch empfangen, so kann die Viterbi–Decodierung durch das nachfolgende Trellis veranschaulicht werden. Der Endwert der Fehlergröße ist ${\it \Gamma}_5(S_0) = 0$, und der Viterbi–Decoder entscheidet mit Sicherheit richtig: $\underline{z} = \underline{x}  ⇒  \underline{\upsilon} = \underline{u}$.

Trellis ohne Fehler/mit 3 Fehlern

Für das untere Trellis gehen wir ebenfalls von $\underline{u} = (0, \, 0, \, 0, \, 0, \, 0)  ⇒  \underline{x} = (00, \, 00, \, 00, \, 00, \, 00)$ aus. Empfangen wird aber nun $\underline{y} = (00, \, 00, \, 00, \, 11, \, 01)$. Trotzdem gilt ${\it \Gamma}_5(S_0) = 0$. Das Beispiel belegt, dass die beiden ersten Aussagen falsch sind. Richtig ist hier nur der Lösungsvorschlag 3, da das Ereignis „Kein Übertragungsfehler” sehr viel wahrscheinlicher ist als drei Fehler an genau vorgegebenen Positionen.

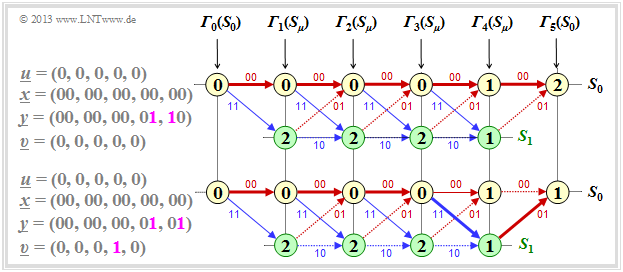
(4)  Richtig sind alle Antworten. Wenn man sicher weiß, dass nur ein Übertragungsfehler aufgetreten ist, funktioniert bei einem Faltungscode mit der freien Distanz $d_{\rm F} = 3$ der Viterbi–Algorithmus perfekt, egal, an welcher Position der Fehler aufgetreten ist.

(5)  Keiner der Lösungsvorschläge ist richtig, wie aus den nachfolgenden Beispielen zu erkennen ist.

Trellis mit 2 Fehlern