Aufgaben:Exercise 3.10Z: Maximum Likelihood Decoding of Convolutional Codes

• Return to book

Betrachtetes Systemmodell

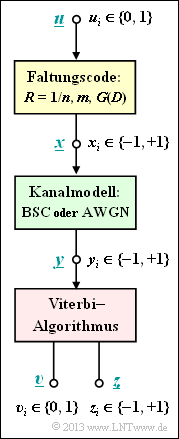
Der Viterbi–Algorithmus stellt die bekannteste Realisierungsform für die Maximum–Likelihood–Decodierung eines Faltungscodes dar. Wir gehen hier von folgendem Modell aus:

• Die Informationssequenz $\underline{u}$ wird durch einen Faltungscode in die Codesequenz $\underline{x}$ umgesetzt. Es gelte $u_i ∈ \{0, \, 1\}$. Dagegen werden die Codesymbole bipolar dargestellt   ⇒   $x_i ∈ \{–1, \, +1\}$.
• Der Kanal sei durch das BSC–Modell gegeben  ⇒  $y_i ∈ \{–1, \, +1\}$ oder es wird der AWGN–Kanal vorausgesetzt   ⇒   reellwertige Empfangswerte $y_i$.
• Bei gegebener Empfangssequenz $\underline{y}$ entscheidet sich der Viterbi–Algorithmus für die Codesequenz $\underline{z}$ entsprechend

$$\underline{z} = {\rm arg} \max_{\underline{x}_{\hspace{0.03cm}i} \hspace{0.03cm} \in \hspace{0.05cm} \mathcal{C}} \hspace{0.1cm} {\rm Pr}( \underline{x}_{\hspace{0.03cm}i} |\hspace{0.05cm} \underline{y} ) \hspace{0.05cm}.$$

• Dies entspricht dem Maximum–a–posteriori (MAP)–Kriterium. Sind die Informationssequenzen $\underline{u}$ gleichwahrscheinlich, so geht dieses in das etwas einfachere Maximum–Likelihood–Kriterium über:

$$\underline{z} = {\rm arg} \max_{\underline{x}_{\hspace{0.03cm}i} \hspace{0.05cm} \in \hspace{0.05cm} \mathcal{C}} \hspace{0.1cm} {\rm Pr}( \underline{y} \hspace{0.05cm}|\hspace{0.05cm} \underline{x}_{\hspace{0.03cm}i} ) \hspace{0.05cm}.$$

• Als weiteres Ergebnis gibt der Viterbi–Algorithmus zusätzlich die Sequenz $\underline{\upsilon}$ als Schätzung für die Informationssequenz $\underline{u}$ aus.

In dieser Aufgabe soll der Zusammenhang zwischen der Hamming–Distanz $d_{\rm H}(\underline{x}, \, \underline{y})$ sowie der Euklidischen Distanz

$$d_{\rm E}(\underline{x} \hspace{0.05cm}, \hspace{0.1cm}\underline{y}) = \sqrt{\sum_{i=1}^{L} \hspace{0.2cm}(x_i - y_i)^2}\hspace{0.05cm}$$

ermittelt werden. Anschließend ist das obige ML–Kriterium mit

• der Hamming–Distanz $d_{\rm H}(\underline{x}, \, \underline{y})$,
• der Euklidischen Distanz $d_{\rm E}(\underline{x}, \, \underline{y})$, und
• dem Korrelationswert $〈 x \cdot y 〉$ zu formulieren.

Hinweise:

• Die Aufgabe bezieht sich auf das Kapitel Decodierung von Faltungscodes.
• Bezug genommen wird insbesondere auf die Seite Viterbi–Algorithmus – basierend auf Korrelation und Metriken.
• Zur Vereinfachung wird auf Tilden und Apostroph verzichtet.
• Weitere Informationen zu diesem Thema finden Sie auf folgenden Seiten dieses Buches:
  • MAP– und ML–Kriterium,
  • ML–Entscheidung beim BSC–Kanal,
  • ML–Entscheidung beim AWGN–Kanal,
  • Decodierung linearer Blockcodes.

Fragebogen

1

Wie hängen $d_{\rm H}(\underline{x}, \, \underline{y})$ und $d_{\rm E}(\underline{x}, \, \underline{y})$ beim BSC–Modell zusammen?

	Es gilt $d_{\rm H}(\underline{x}, \, \underline{y}) = d_{\rm E}(\underline{x}, \, \underline{y})$.
	Es gilt $d_{\rm H}(\underline{x}, \, \underline{y}) = d_{\rm E}^2(\underline{x}, \, \underline{y})$.
	Es gilt $d_{\rm H}(\underline{x}, \, \underline{y}) = d_{\rm E}^2(\underline{x}, \, \underline{y})/4$.

2

Welche der Gleichungen beschreiben die ML–Decodierung beim BSC–Modell? Die Minimierung/Maximierung bezieht sich jeweils auf alle $\underline{x} ∈\mathcal{ C}$.

	$\underline{z} = \arg \min {d_{\rm H}(\underline{x}, \, \underline{y})}$,
	$\underline{z} = \arg \min {d_{\rm E}(\underline{x}, \, \underline{y})}$,
	$\underline{z} = \arg \min {d_{\rm E}^2(\underline{x}, \, \underline{y})}$,

3

Welche Gleichung beschreibt die ML–Entscheidung beim BSC–Modell?

	$\underline{z} = \arg \min 〈 \underline{x} \cdot \underline{y} 〉$,
	$\underline{z} = \arg \max 〈 \underline{x} \cdot \underline{y} 〉$.

4

Welche Gleichungen gelten für die ML–Entscheidung beim AWGN?

	$\underline{z} = \arg \min {d_{\rm H}(\underline{x}, \, \underline{y})}$,
	$\underline{z} = \arg \min {d_{\rm E}(\underline{x}, \, \underline{y})}$,
	$\underline{z} = \arg \max 〈 \underline{x} \cdot \underline{y} 〉$.

Musterlösung

Solution

(1)  Richtig ist der Lösungsvorschlag 3:

• Die zwei Binärfolgen seien $\underline{x}$ und $\underline{y}$ mit $x_i ∈ \{-1, \, +1\}, \ y_i ∈ \{-1, \, +1\}$. Die Folgenlänge sei jeweils $L$.
• Die Hamming–Distanz $d_{\rm H}(\underline{x}, \, \underline{y})$ gibt die Anzahl der Bit an, in denen sich $\underline{x}$ und $\underline{y}$ unterscheiden, für die also $x_i \, - y_i = ±2$   ⇒   $(x_i \, - y_i)^2 = 4$ gilt.
• Gleiche Symbole $(x_i = y_i)$ tragen zur Hamming–Distanz nicht bei und ergeben $(x_i \, – y_i)^2 = 0$. Entsprechend dem Lösungsvorschlag 3 kann daher geschrieben werden:

$$d_{\rm H}(\underline{x} \hspace{0.05cm}, \hspace{0.1cm}\underline{y}) = \frac{1}{4} \cdot \sum_{i=1}^{L} \hspace{0.2cm}(x_i - y_i)^2= \frac{1}{4} \cdot d_{\rm E}^2(\underline{x} \hspace{0.05cm}, \hspace{0.1cm}\underline{y})\hspace{0.05cm}.$$

(2)  Alle Lösungsvorschläge sind richtig:

• Beim BSC–Modell ist es allgemein üblich, zum gegebenen Empfangsvektor $\underline{y}$ das Codewort $\underline{x}$ mit der kleinsten Hamming–Distanz $d_{\rm H}(\underline{x}, \, \underline{y})$ auszuwählen:

$$\underline{z} = {\rm arg} \min_{\underline{x} \hspace{0.05cm} \in \hspace{0.05cm} \mathcal{C}} \hspace{0.1cm} d_{\rm H}(\underline{x} \hspace{0.05cm}, \hspace{0.1cm}\underline{y})\hspace{0.05cm}.$$

• Entsprechend der Teilaufgabe (1) gilt aber auch:

$$\underline{z} = {\rm arg} \min_{\underline{x} \hspace{0.05cm} \in \hspace{0.05cm} \mathcal{C}} \hspace{0.1cm} d_{\rm E}^{\hspace{0.15cm}2}(\underline{x} \hspace{0.05cm}, \hspace{0.1cm}\underline{y})/4 \hspace{0.2cm}\Rightarrow \hspace{0.2cm} \underline{z} = {\rm arg} \min_{\underline{x} \hspace{0.05cm} \in \hspace{0.05cm} \mathcal{C}} \hspace{0.1cm} d_{\rm E}^{\hspace{0.15cm}2}(\underline{x} \hspace{0.05cm}, \hspace{0.1cm}\underline{y}) \hspace{0.2cm}\Rightarrow \hspace{0.2cm} \underline{z} = {\rm arg} \min_{\underline{x} \hspace{0.05cm} \in \hspace{0.05cm} \mathcal{C}} \hspace{0.1cm} d_{\rm E}(\underline{x} \hspace{0.05cm}, \hspace{0.1cm}\underline{y}) \hspace{0.05cm}.$$

• Der Faktor $1/4$ spielt für die Minimierung keine Rolle. Da $d_{\rm E}(\underline{x}, \, \underline{y}) ≥ 0$ ist, ist es auch egal, ob die Minimierung hinsichtlich $d_{\rm E}(\underline{x}, \, \underline{y})$ oder $d_{\rm E}^2(\underline{x}, \, \underline{y})$ vorgenommen wird.

(3)  Richtig ist der Lösungsvorschlag 2:

• Das Quadrat der Euklidischen Distanz kann wie folgt ausgedrückt werden:

$$d_{\rm E}^{\hspace{0.15cm}2}(\underline{x} \hspace{0.05cm}, \hspace{0.1cm}\underline{y}) = \sum_{i=1}^{L} \hspace{0.2cm}(x_i - y_i)^2 = \hspace{0.1cm}\sum_{i=1}^{L} \hspace{0.1cm} x_i^{\hspace{0.15cm}2} \hspace{0.1cm}+ \hspace{0.1cm}\sum_{i=1}^{L} \hspace{0.1cm} y_i^{\hspace{0.15cm}2} \hspace{0.1cm}-2 \cdot \sum_{i=1}^{L} \hspace{0.1cm} x_i \cdot y_i \hspace{0.05cm}.$$

• Die beiden ersten Summanden sind jeweils gleich $L$ und müssen für die Minimierung nicht berücksichtigt werden.
• Für den letzten Ausdruck in dieser Gleichung kann $–2 \cdot 〈 \underline{x}, \, \underline{y} 〉$ geschrieben werden.
• Aufgrund des negativen Vorzeichens wird aus der Minimierung eine Maximierung   ⇒   Antwort 2.

(4)  Richtig sind die Lösungsvorschläge 2 und 3.:

• Für den AWGN–Kanal kann im Gegensatz zum BSC keine Hamming–Distanz angegeben werden.
• Ausgehend von der Gleichung

$$d_{\rm E}^{\hspace{0.15cm}2}(\underline{x} \hspace{0.05cm}, \hspace{0.1cm}\underline{y}) = \hspace{0.1cm}\sum_{i=1}^{L} \hspace{0.1cm} x_i^{\hspace{0.15cm}2} \hspace{0.1cm}+ \hspace{0.1cm}\sum_{i=1}^{L} \hspace{0.1cm} y_i^{\hspace{0.15cm}2} \hspace{0.1cm}-2 \cdot \sum_{i=1}^{L} \hspace{0.1cm} x_i \cdot y_i$$

gelten für den ersten und letzten Summanden die gleichen Aussagen wie für das BSC–Modell – siehe Teilaufgabe (3).

• Für den mittleren Summanden gilt mit $y_i = x_i + n_i$ und $x_i ∈ \{–1, \, +1\}$:

$$\sum_{i=1}^{L} \hspace{0.1cm} y_i^{\hspace{0.15cm}2} = \hspace{0.1cm}\sum_{i=1}^{L} \hspace{0.1cm} x_i^{\hspace{0.15cm}2} \hspace{0.1cm}+ \hspace{0.1cm}\sum_{i=1}^{L} \hspace{0.1cm} n_i^{\hspace{0.15cm}2} \hspace{0.1cm}+2 \cdot \sum_{i=1}^{L} \hspace{0.1cm} x_i \cdot n_i \hspace{0.05cm}.$$

• Der erste Summand ergibt wieder $L$, der zweite ist proportional zur Rauschleistung und der letzte Term verschwindet, da $\underline{x}$ und $\underline{n}$ unkorreliert sind.
• Für die Minimerung von $d_{\rm E}(\underline{x}, \, \underline{y})$ muss also die Summe über $y_i^2$ nicht berücksichtigt werden, da kein Bezug zu den Codesequenzen $\underline{x}$ besteht.