Aufgaben:Exercise 4.2: Channel Log Likelihood Ratio at AWGN

• Return to book

Bedingte Gaußfunktionen

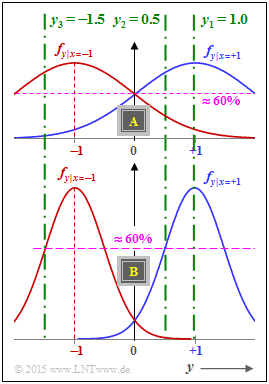
Wir betrachten zwei Kanäle A und B, jeweils mit

• binärem bipolaren Eingang $x ∈ \{+1, \, -1\}$, und
• wertkontinuierlichem Ausgang $y ∈ {\rm \mathcal{R}}$ (reelle Zahl).

Die Grafik zeigt für beide Kanäle

• als blaue Kurve die Dichtefunktionen $f_{y\hspace{0.05cm}|\hspace{0.05cm}x=+1}$,
• als rote Kurve die Dichtefunktionen $f_{y\hspace{0.05cm}|\hspace{0.05cm}x=-1}$.

Im Theorieteil wurde für diese AWGN–Konstellation der Kanal–$L$–Wert (englisch: Channel Log Likelihood Ratio, oder kurz Channel LLR) wie folgt hergeleitet:

$$L_{\rm K}(y) = L(y\hspace{0.05cm}|\hspace{0.05cm}x) = {\rm ln} \hspace{0.15cm} \frac{{\rm Pr}(y \hspace{0.05cm}|\hspace{0.05cm}x=+1) }{{\rm Pr}(y \hspace{0.05cm}|\hspace{0.05cm}x = -1)} \hspace{0.05cm}.$$

Wertet man diese Gleichung analytisch aus, so erhält man mit der Proportionalitätskonstanten $K_{\rm L} = 2/\sigma^2$:

$$L_{\rm K}(y) = K_{\rm L} \cdot y \hspace{0.05cm}.$$

Hinweise:

• Die Aufgabe gehört zum Kapitel Soft–in Soft–out Decoder.
• Bezug genommen wird insbesondere auf die Seiten Zuverlässigkeitsinformation – Log Likelihood Ratio sowie AWGN–Kanal bei binärem Eingang.
• Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.

Fragebogen

1

Welche Eigenschaften weisen die in der Grafik dargestellten Kanäle auf?

	Sie beschreiben die Binärübertragung bei Gaußscher Störung.
	Die Bitfehlerwahrscheinlichkeit ohne Codierung ist ${\rm Q}(1/\sigma)$.
	Das Kanal–LLR ist als $L_{\rm K}(y) = K_{\rm L} \cdot y$ darstellbar.

2

Welche Konstante $K_{\rm L}$ kennzeichnet den Kanal A?

$K_{\rm L} \ = \ $

3

Welche Informationen liefern bei Kanal A die Empfangswerte $y_1 = 1, \ y_2 = 0.5$, $y_3 = \, -1.5$ über die gesendeten Binärsymbole $x_1, \ x_2$ bzw. $x_3$?

	$y_1 = 1.0$ sagt aus, dass wahrscheinlich $x_1 = +1$ gesendet wurde.
	$y_2 = 0.5$ sagt aus, dass wahrscheinlich $x_2 = +1$ gesendet wurde.
	$y_3 = \, -1.5$ sagt aus, dass wahrscheinlich $x_3 = \, -1$ gesendet wurde.
	Die Entscheidung „$y_1 → x_1$” ist sicherer als „$y_2 → x_2$”.
	Die Entscheidung „$y_1 → x_1$” ist sicherer als „$y_3 → x_3$”.

4

Welche $K_{\rm L}$ kennzeichnet den Kanal B?

$K_{\rm L} \ = \ $

5

Welche Informationen liefern bei Kanal B die Empfangswerte $y_1 = 1, \ y_2 = 0.5$, $y_3 = -1.5$ über die gesendeten Binärsymbole $x_1, \ x_2$ bzw. $x_3$?

	Für $x_1, \ x_2, \ x_3$ wird gleich entschieden wie bei Kanal A.
	Die Schätzung „$x_2 = +1$” ist viermal sicherer als bei Kanal A.
	Die Schätzung „$x_3 = \, -1$” bei Kanal A ist zuverlässiger als die Schätzung „$x_2 = +1$” bei Kanal B.

Musterlösung

Solution

(1)  Alle Lösungsvorschläge sind richtig:

• Die Übergangsgleichung lautet stets $y = x + n$, wobei $x ∈ \{+1, \, -1\}$ gilt und $n$ eine Gaußsche Zufallsgröße mit Streuung $\sigma$   ⇒   Varianz $\sigma^2$ angibt   ⇒   AWGN–Kanal.
• Die AWGN–Bitfehlerwahrscheinlichkeit berechnet sich mit der Streuung $\sigma$ zu ${\rm Q}(1/\sigma)$ wobei ${\rm Q}(x)$ die komplementäre Gaußsche Fehlerfunktion bezeichnet.
• Für jeden AWGN–Kanal ergibt sich entsprechend dem Theorieteil das Kanal–LLR stets zu $L_{\rm K}(y) = L(y|x) = K_{\rm L} \cdot y$. Die Konstante $K_{\rm L}$ ist für die beiden Kanäle allerdings unterschiedlich.

(2)  Beim AWGN–Kanal gilt $L_{\rm K}(y) = K_{\rm L} \cdot y$ mit der Konstanten $K_{\rm L} = 2/\sigma^2$. Die Streuung $\sigma$ kann aus der Grafik auf der Angabenseite als der Abstand der Wendepunkte innerhalb der Gaußkurven von ihren jeweiligen Mittelpunkten abgelesen werden. Beim Kanal A ergibt sich $\sigma = 1$.

Zum gleichen Ergebnis kommt man durch Auswertung der Gaußfunktion

$$\frac{f_{\rm G}( y = \sigma)}{f_{\rm G}( y = 0)} = {\rm e} ^{ - y^2/(2\sigma^2) } \Bigg |_{\hspace{0.05cm} y \hspace{0.05cm} = \hspace{0.05cm} \sigma} = {\rm e} ^{ -0.5} \approx 0.6065\hspace{0.05cm}.$$

Das bedeutet: Beim Abszissenwert $y = \sigma$ ist die mittelwertfreie Gaußfunktion $f_{\rm G}(y)$ auf $60.65\%$ ihres Maximalwertes abgeklungen. Somit gilt für die Konstante beim Kanal A:   $K_{\rm L} = 2/\sigma^2 \ \underline{= 2}$.

(3)  Richtig sind die Lösungsvorschläge 1 bis 4:

• Wir geben zunächst die jeweiligen $L$–Werte von Kanal A an:

$$L_{\rm K}(y_1 = +1.0) = +2\hspace{0.05cm},\hspace{0.3cm} L_{\rm K}(y_2 = +0.5) = +1\hspace{0.05cm},\hspace{0.3cm} L_{\rm K}(y_3 = -1.5) = -3\hspace{0.05cm}. $$

• Daraus ergeben sich folgende Konsequenzen:

• Die Entscheidung für das (wahrscheinlichste) Codebit $x_i$ wird aufgrund des Vorzeichens von $L_{\rm K}(y_i)$ getroffen: $x_1 = +1, \ x_2 = +1, \ x_3 = \, -1$   ⇒   die Lösungsvorschläge 1, 2 und 3 sind richtig.
• Die Entscheidung „$x_1 = +1$” ist wegen $|L_{\rm K}(y_1)| > |L_{\rm K}(y_3)|$ zuverlässiger als die Entscheidung „$x_2 = +1$”   ⇒   Lösungsvorschlag 4 ist ebenfalls richtig.
• Die Entscheidung „$x_1 = +1$” ist aber weniger zuverlässig als die Entscheidung „$x_3 = \, –1$”, da $|L_{\rm K}(y_1)|$ kleiner als $|L_{\rm K}(y_3)|$ ist   ⇒   Lösungsvorschlag 5 ist falsch.

Dies kann man auch so interpretieren: Der Quotient zwischen dem roten und dem blauen WDF–Wert ist bei $y_3 = \, -1.5$ größer als der Quotient zwischen dem blauen und dem roten WDF–Wert bei $y_1 = +1$.

(4)  Nach gleichen Überlegungen wie bei der Teilaufgabe (2) ergibt sich für die Streuung von Kanal B:   $\sigma = 1/2 \ \Rightarrow \ K_{\rm L} = 2/\sigma^2 \ \underline{= 8}$.

(5)  Für den Kanal B gilt:   $L_{\rm K}(y_1 = +1.0) = +8, \ L_{\rm K}(y_2 = +0.5) = +4$ und $L_{\rm K}(y_3 = \, -1.5) = \, -12$.

Damit ist offensichtlich, dass die beiden ersten Lösungsvorschläge zutreffen, nicht aber der dritte, weil

$$|L_{\rm K}(y_3 = -1.5, {\rm Kanal\hspace{0.15cm} A)}| = 3 \hspace{0.5cm} <\hspace{0.5cm} |L_{\rm K}(y_2 = 0.5, {\rm Kanal\hspace{0.15cm} B)}| = 4\hspace{0.05cm} . $$