Difference between revisions of "Examples of Communication Systems/xDSL as Transmission Technology"
| Line 88: | Line 88: | ||
Da sich die Hersteller von 1997 bis 2003 auch aus patentrechtlichen Gründen auf keinen gemeinsamen Standard einigen konnten (man spricht in diesem Zusammenhang sogar von ''Line Code Wars''), kam es lange Zeit zur Koexistenz beider konkurrierender Verfahren. Bei den so genannten DSL–Olympics 2003 wurde schließlich die Entscheidung zugunsten von DMT getroffen, | Da sich die Hersteller von 1997 bis 2003 auch aus patentrechtlichen Gründen auf keinen gemeinsamen Standard einigen konnten (man spricht in diesem Zusammenhang sogar von ''Line Code Wars''), kam es lange Zeit zur Koexistenz beider konkurrierender Verfahren. Bei den so genannten DSL–Olympics 2003 wurde schließlich die Entscheidung zugunsten von DMT getroffen, | ||
| − | *einerseits wegen der etwas besseren Performance allgemein, | + | *einerseits wegen der etwas besseren „Performance” allgemein, |
*insbesondere aber wegen der höheren Robustheit gegenüber Schmalbandstörungen. | *insbesondere aber wegen der höheren Robustheit gegenüber Schmalbandstörungen. | ||
Insbesondere für die USA (viele Telefonfreileitungen und damit verbundene Probleme mit eingekoppelten Funksignalen) hat das zweite Argument eine große Rolle gespielt. | Insbesondere für die USA (viele Telefonfreileitungen und damit verbundene Probleme mit eingekoppelten Funksignalen) hat das zweite Argument eine große Rolle gespielt. | ||
| − | Die heutigen (2010) in Deutschland vorwiegend angebotenen xDSL–Varianten ADSL2(+) und | + | |
| − | Zunächst sollen aber in aller Kürze | + | Die heutigen (2010) in Deutschland vorwiegend angebotenen xDSL–Varianten ADSL2(+) und VDSL(2) basieren alle auf dem ''Discrete Multitone Transmission''–Verfahren, wobei aber die einzelnen Subträger durchaus mit QAM–Signalen belegt sein können. |
| + | Zunächst sollen aber in aller Kürze die Systeme $\rm xDSL–QAM$ und $\rm xDSL–CAP$ betrachtet werden. | ||
Revision as of 17:22, 6 February 2018
Contents
- 1 Mögliche Bandbreitenbelegungen für xDSL
- 2 ADSL–Bandbreitenbelegung in Deutschland
- 3 VDSL(2)–Bandbreitenbelegung
- 4 Übertragungsverfahren im Überblick
- 5 Grundlagen der Quadratur–Amplitudenmodulation
- 6 Mögliche QAM–Signalraumkonstellationen
- 7 Carrierless Amplitude Phase Modulation (CAP)
- 8 Grundlagen von DMT – Discrete Multitone Transmission
- 9 DMT–Realisierung mit IDFT/DFT
- 10 Aufgaben zu Kapitel 2.3
Mögliche Bandbreitenbelegungen für xDSL
Die xDSL–Spezifikationen lassen den Betreibern viele Freiheiten hinsichtlich der Belegung.
$\text{Definition:}$ Zur notwendigen Richtungstrennung der xDSL–Signalübertragung nach
- Abwärtsrichtung vom Anbieter zum Kunden (Downstream mit möglichst hoher Datenrate),
- Aufwärtsrichtung vom Kunden zum Anbieter (Upstream mit meist niedrigerer Datenrate)
wurden hierfür zwei Varianten standardisiert:
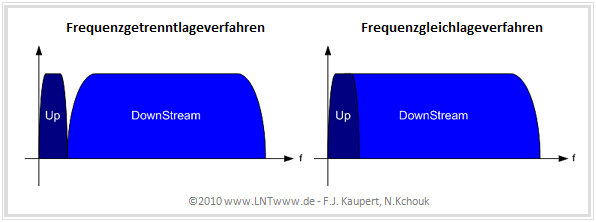
- Beim Frequenzgetrenntlageverfahren werden die Datenströme für die beiden Richtungen in zwei voneinander getrennten Frequenzbändern übertragen mit dem Vorteil, dass zur Trennung der Übertragungsrichtungen ein einfaches Filter genügt, was die technische Realisierung vereinfacht.
- Beim Frequenzgleichlageverfahren überlagern sich in einem bestimmten Teil die Spektren von Upstream und Downstream. Die Trennung erfolgt hier mit Hilfe einer Echokompensationsschaltung. Vorteile des Verfahrens sind der geringere Bandbreitenbedarf bei höheren (und damit stärker gedämpften) Frequenzen sowie eine größere Reichweite.
Die Grafik stellt diese beiden Möglichkeiten vergleichend gegenüber.
Grundsätzlich überlassen die Spezifikationen den Entwicklern/Betreibern die Entscheidung,
- xDSL alleine auf der Teilnehmeranschlussleitung zu betreiben, oder
- einen Mischbetrieb von xDSL mit den Telefondiensten POTS (Plain Old Telephone Service) oder ISDN (Integrated Services Digital Network) zu ermöglichen, und somit
- den von den beiden Telefondiensten belegten unteren Frequenzbereich für xDSL auszuschließen oder auch zu belegen.
ADSL–Bandbreitenbelegung in Deutschland
Wegen der technisch deutlich einfacheren Realisierbarkeit fiel in Deutschland für ADSL und ADSL2+ die Entscheidung zugunsten
- des Frequenzgetrenntlageverfahrens,
- die generelle Reservierung des unteren Frequenzbereichs für ISDN.
Das Frequenzgleichlageverfahren wird zwar teilweise noch verwendet, aber eher selten.
Bei den Übertragungsverfahren QAM (Quadratur–Amplitudenmodulation) und CAP (Carrierless Amplitude Phase Modulation) wird die für DSL verfügbare Bandbreite nicht weiter zerlegt. Dagegen werden beim Mehrträgerverfahren DMT (Discrete Multitone Transmission) der Aufwärtskanal und der Abwärtskanal in $N_{\rm Up}$ bzw. $N_{\rm Down}$ Subkanäle (englisch: Bins) zu je 4.3125 kHz aufgeteilt.
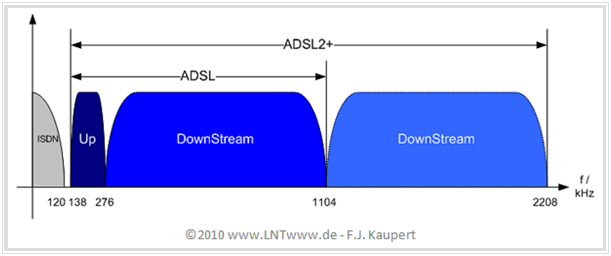
Außerdem ist zu dieser Grafik anzumerken:
- Telefondienste (POTS bzw. ISDN) und xDSL liegen in verschiedenen Frequenzbändern, was die gegenseitigen Störungen im Bündelkabel minimiert. Das signalstärkere ISDN stört somit nicht das parallel laufende xDSL und umgekehrt.
- Der untere Frequenzbereich bis 120 kHz wurde für ISDN (wahlweise POTS) reserviert. Dieser Wert ergibt sich aus der ersten Nullstelle des ISDN–Spektrums mit 4B3T–Codierung. Oberhalb von 120 kHz wird das ISDN–Spektrum vollständig unterdrückt.
- Zur Trennung von Telefon– und xDSL–Signal wird an beiden Enden der Zweidrahtleitung ein Splitter eingesetzt, der je ein Tiefpassfilter und ein Hochpassfilter beinhaltet und auch die folgende Frequenzlücke bis 138 kHz berücksichtigt.
- Nach dieser Belegungslücke folgt das ADSL–Upstream-Band von 138 kHz bis 276 kHz. Diese Bandbreite erlaubt die Übertragung von $N_{\rm Up} = 32$ Subträgern zu je 4.3125 kHz. Dieser Wert ergibt sich aus der Rahmenübertragungsgeschwindigkeit.
- Der anschließende Downstream–Bereich reicht bei ADSL bis 1104 kHz, womit $N_{\rm Down} = 256$ Subträger realisiert werden können. Die Trennung von Auf– und Abwärtskanal bei xDSL erfolgt über ein Bandpassfilter im Modem.
- Allerdings dürfen die ersten 64 Subträger (dies entspricht 276 kHz) nicht belegt werden. Beim Frequenzgleichlageverfahren wären nur 32 Subträger auszusparen, wobei zu berücksichtigen ist, dass die Trennung von Aufwärts– und Abwärtsrichtung eine aufwändigere Realisierung erfordert.
- Bei ADSL2+ ist die Systembandbreite gleich 2208 kHz ⇒ $N_{\rm Down} = 512$ Subträger. Die Anzahl der auszusparenden Bins bleibt gegenüber ADSL unverändert. Berücksichtigt man, dass zwei Bins von Kontrollfunktionen (beispielsweise zur Synchronisation von Sender und Empfänger) belegt werden, so verbleiben $190$ (ADSL) bzw. $446$ (ADSL2+) Downstream–Kanäle für Nutzer.
- Die in Deutschland vorgeschriebene ISDN–Reservierung hat für xDSL allerdings die Konsequenz, dass die niedrigen Frequenzen, die bei einer Kupferleitung mit Abstand am wenigsten gedämpft werden und damit eigentlich am besten geeignet wären, nicht genutzt werden können.
- Aus der Frequenzanordnung erkennt man weiterhin, dass die Downstream–Subkanäle stärker gedämpft werden als die Upstream–Subkanäle (höhere Frequenzen) und demzufolge ein kleineres Signal–zu–Rauschleistungsverhältnis (SNR) aufweisen.
- Die Entscheidung „Upstream unterhalb Downstream” hängt damit zusammen, dass der Ausfall von Downstream–Kanälen nur eine vergleichsweise geringe Auswirkung auf die Übertragungsrate hat. Im Upstream würde sich ein solcher Ausfall prozentual viel stärker bemerkbar machen.
VDSL(2)–Bandbreitenbelegung
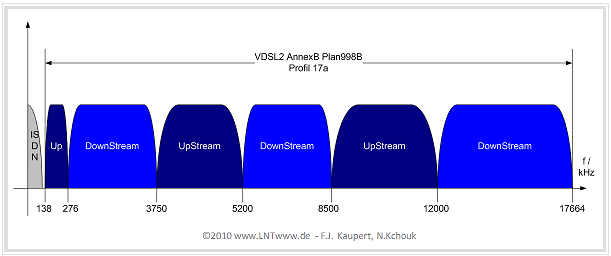
Für VDSL(2) hat die ITU mehrere Profile festgelegt. Für die in Deutschland eingesetzten Systeme gilt zum Zeitpunkt der Erstellung dieses Kapitels (2010) die in der Grafik angegebene Frequenzbandbelegung gemäß dem VDSL(2) Plan 998b – Profil 17a (Annex B) der ITU. Die (leicht) hellere Farbgebung bei den höheren Frequenzen soll darauf hinweisen, dass diese Kanäle stärker gedämpft werden.
Ohne Anspruch auf Vollständigkeit lässt sich dieser Belegungsplan wie folgt charakterisieren:
- Um höhere Bitraten zu erreichen, werden hier achtmal so viele Bins verwendet als bei ADSL2+. Damit beträgt die Systembandbreite 8 · 2208 MHz = 17664 MHz, womit Übertragungsraten bis zu 100 Mbit/s (abhängig von Kabellänge und –beschaffenheit) ermöglicht werden.
- Auch hier gilt, dass die Frequenzbänder für die Upstream–Subkanäle immer bei den niedrigeren Frequenzen angeordnet sind, da die größere Kabeldämpfung (mit der Frequenz zunehmend) beim Upstream einen prozentual größeren Einfluss auf die Gesamtbitrate hat als beim Downstream.
- Bei VDSL(2)–Systemen wird stets das so genannte Frequenzgetrenntlageverfahren verwendet. Eine Überlappung der Upstream– und Downstream–Frequenzbänder ist in der ITU–Spezifikation für VDSL(2) kategorisch ausgeschlossen.
- Bei den VDSL–Systemen in Deutschland sind die unteren Frequenzen wieder für ISDN reserviert. Danach folgen abwechselnd Bereiche für Upstream und Downstream. Aus den angegebenen Bereichsgrenzen erkennt man die gegenüber dem Downstream schmäleren Upstream–Bereiche.
- Man erkennt eine abwechselnde Anordnung von Upstream– und Downstreambereichen. Ein Grund hierfür ist, dass bei diesem breiten Spektrum vermieden werden soll, dass eine Richtung (zum Beispiel abwärts) nur stark gedämpfte (also hohe) Frequenzen zugewiesen bekommt.
- Die VDSL(2)–Spezifikation sieht Belegungspläne bis zu Systembandbreiten von 30 MHz (nach dem Profil 30a) vor, die Übertragungsraten bis etwa 200 Mbit/s auf kurzen Strecken ermöglichen sollen. Dafür wird auch die Bandbreite der einzelnen Subkanäle gegenüber ADSL auf 8.625 kHz verdoppelt.
- Alle Belegungspläne werden mit verschiedenen Masken für das Leistungsdichtespektrum versehen, um so die maximale Sendeleistung und damit auch die Störung benachbarter Systeme im Kabelbündel (Nebensprechen) zu begrenzen.
Übertragungsverfahren im Überblick
Zu Beginn der verschiedenen Standardisierungsprozeduren für die einzelnen xDSL–Varianten wurden als Basis verschiedene Übertragungsverfahren festgelegt:
- Pulscodemodulation (PCM) für ISDN sowie Trellis Coded–Pulse Amplitude Modulation für HDSL2 und SHDSL/SDSL,
- Quadratur–Amplitudenmodulation (QAM) für QAM–ADSL und QAM–VDSL,
- Carrierless Amplitude Phase Modulation (CAP) für CAP–HDSL und CAP–ADSL,
- Discrete Multitone Transmission (DMT) für ADSL, ADSL2, ADSL 2+, VDSL und VDSL2.
Mit zunehmender Forderung des Marktes nach höheren Übertragungsraten und den damit verbundenen Anforderungen kristallisierten sich zwei geeignete Hauptverfahren heraus, nämlich $\rm QAM/CAP$ und $\rm DMT$.
Da sich die Hersteller von 1997 bis 2003 auch aus patentrechtlichen Gründen auf keinen gemeinsamen Standard einigen konnten (man spricht in diesem Zusammenhang sogar von Line Code Wars), kam es lange Zeit zur Koexistenz beider konkurrierender Verfahren. Bei den so genannten DSL–Olympics 2003 wurde schließlich die Entscheidung zugunsten von DMT getroffen,
- einerseits wegen der etwas besseren „Performance” allgemein,
- insbesondere aber wegen der höheren Robustheit gegenüber Schmalbandstörungen.
Insbesondere für die USA (viele Telefonfreileitungen und damit verbundene Probleme mit eingekoppelten Funksignalen) hat das zweite Argument eine große Rolle gespielt.
Die heutigen (2010) in Deutschland vorwiegend angebotenen xDSL–Varianten ADSL2(+) und VDSL(2) basieren alle auf dem Discrete Multitone Transmission–Verfahren, wobei aber die einzelnen Subträger durchaus mit QAM–Signalen belegt sein können. Zunächst sollen aber in aller Kürze die Systeme $\rm xDSL–QAM$ und $\rm xDSL–CAP$ betrachtet werden.
Grundlagen der Quadratur–Amplitudenmodulation
Die folgende Grafik zeigt das Referenzmodell für QAM–ADSL, wobei wir uns hier nur mit den beiden roten Funktionsblöcken QAM–Modulator und QAM–Demodulator beschäftigen wollen.
Die Trägerfrequenz $f_T$ liegt jeweils innerhalb des spezifizierten Auf– und Abwärts–Bandes der jeweiligen xDSL–Variante. Sie wird ebenso wie die Signalraumgröße (zwischen 4 und 256 Signalraumpunkte) und die Symbolrate durch Kanalmessungen bei der Initialisierung der Übertragung festgelegt.
Für QAM–ADSL wurden folgende Symbolraten (in kBaud = 1000 Symbole/s) festgelegt:
- 20, 40, 84, 100, 120, 136 im Upstream,
- 40, 126, 160, 252, 336, 504, 806.4, 1008 im Downstream.
Das QAM–Prinzip wurde bereits im Kapitel 4.3 des Buches „Modulationsverfahren” ausführlich beschrieben. Hier folgt nur eine kurze Zusammenfassung anhand der folgenden Grafik bezieht:
- QAM ist ein Einträgermodulationsverfahren um die Trägerfrequenz $f_T$. Zunächst erfolgt eine blockweise Seriell–/Parallelwandlung des Bitstroms und die Signalraumzuordnung.
- Aus jeweils $b$ Binärsymbolen werden zwei mehrstufige Amplitudenkoeffizienten $a_{In}$ und $a_{Qn}$ abgeleitet (Inphase– und Quadraturkomponente), wobei beide Koeffizienten jeweils einen von $M = 2^{b/2}$ möglichen Amplitudenwerten annehmen können.
- Das in der Grafik betrachtete Beispiel gilt für die 16–QAM mit $b$ = $M$ = 4 und dementsprechend 16 Signalraumpunkten. Bei einer 256–QAM würde $b$ = 8 und $M$ = 16 gelten ( $2^b = M^2 = 256$ ).
- Die Koeffizienten $a_{In}$ und $a_{Qn}$ werden jeweils einem Diracpuls als Impulsgewichte eingeprägt. Nach der Impulsformung ⇒ Sendegrundimpuls $g_s(t)$ gilt in den Zweigen des Blockschaltbilds:
Für die Impulsformung kommen meist Cosinus–Rolloff–Filter (geringe Bandbreite !) zum Einsatz.
- Anzumerken ist, dass wegen der redundanzfreien Umsetzung die Symboldauer $T$ dieser Signale um den Faktor $b$ größer ist als die Bitdauer $T_{\rm B}$ der binären Eingangsfolge. Im gezeichneten Beispiel (16–QAM) gilt $T = 4 · T_{\rm B}$.
- Das QAM–Sendesignal $s(t)$ ist dann die Summe der beiden mit Cosinus bzw. Minus–Sinus multiplizierten Teilsignale (möglicherweise folgt noch eine Bandbegrenzung, um Interferenzen zu benachbarten Bändern zu verhindern, siehe Grafik):
- Die beiden Zweige (I und Q) können wegen der Orthogonalität von Cosinus– und (Minus–) Sinus als zwei völlig getrennte $M$–stufige ASK–Systeme aufgefasst werden, die sich gegenseitig nicht stören, solange alle Komponenten optimal ausgelegt sind.
- Das bedeutet gleichzeitig: Die Quadratur–Amplitudenmodulation ermöglicht gegenüber einer BPSK (Modulationnur mit Cosinus oder Sinus) eine Verdoppelung der Datenrate bei gleichbleibender Qualität.
Die Grafik zeigt oben das BP–Modell, unten das äquivalente TP–Modell. Man kombiniert Inphase– und Quadraturkoeffizient zum komplexen Amplitudenkoeffizienten $a_n = a_{\text{I}n} + j · a_{\text{Q}n}$ und ersetzt zusätzlich das BP–Signal $s(t)$ durch das äquivalente TP–Signal $s_{\rm TP}(t) = s_{\rm I}(t) + j · s_{\rm Q}(t)$.
Die Darstellung des QAM–Senders und des hier nicht explizit aufgeführten QAM–Empfängers ist Inhalt der Flash–Animation Prinzip der Quadratur–Amplitudenmodulation.
Mögliche QAM–Signalraumkonstellationen
Ein wichtiger QAM–Parameter ist die Anzahl $b$ der Bits, die zum Amplitudenkoeffizientenpaar ( $a_{\rm I}, a_{\rm Q}$ ) verarbeitet werden. Hierbei ist $b$ stets geradzahlig. Ist $b$ = 2, so kann sowohl aI als auch $a_{\m Q}$ nur die beiden Werte ±1 annehmen und es ergibt sich die 4–QAM entsprechend der linken Konstellation in nachfolgender Grafik. Entsprechend einer ITU–Empfehlung gilt dabei die Zuordnung:
Der gelb markierte Punkt 10 ( $a_{\rm I}$ = –1, $a_{\rm Q}$ = 1) steht also für $q_1$ = 1, $q_0$ = 0.
Mit $b = 4$ ⇒ $M = 2^{b/2} = 4$ kommt man zur 16–QAM entsprechend dem rechten Diagramm mit den möglichen Amplitudenkoeffizienten $a_{\rm I}$ ∈ {±3, ±1} und $a_{\rm Q}$ ∈ {±3, ±1}. Dieses lässt sich mit Hilfe des links unten angegebenen Hilfsgrafen ermitteln, wie die nachfolgenden zwei Beispiele verdeutlichen sollen.
- $q_3$ = 1, $q_2$ = 0, $q_1$ = 1, $q_0$ = 1 (gelbe Markierung). Die beiden höchstwertigen Bit (Most Significant Bit, MSB) 10 bestimmen entsprechend dem 4–QAM–Diagramm den Quadranten, in dem das Symbol liegt. Die beiden niederwertigen Bit (11) legen zusammen mit dem Hilfsgrafen den Punkt innerhalb des Quadranten fest. Das Ergebnis ist $a_{\rm I}$ = –1, $a_{\rm Q}$ = +3.
- Entsprechend liefern die Eingangsbits $q_3$ = 0, $q_2$ = 1, $q_1$ = 1, $q_0$ = 0 (grüne Markierung) die Koeffizienten $a_{\rm I}$ = +3, $a_{\rm Q}$ = –3.
Carrierless Amplitude Phase Modulation (CAP)
Carrierless Amplitude Phase Modulation (CAP) ist eine bandbreiteneffiziente Variante der QAM, die sich mit digitalen Signalprozessoren sehr einfach realisieren lässt. Der Unterschied zur QAM liegt einzig darin, dass auf eine Modulation mit einem Trägersignal verzichtet werden kann.
Anstelle der Multiplikation mit Cosinus und Minus–Sinus wird hier eine digitale Filterung vorgenommen. $g_{\rm I}(t)$ und $g_{\rm Q}(t)$ sind die um $π/2$ phasenverschobenen Impulsantworten zweier transversaler Bandpassfilter mit gleicher Amplitudencharakteristik. Beide sind zueinander orthogonal, das heißt, dass das Integral des Produkts $g_{\rm I}(t) · g_{\rm Q}(t)$ über eine Symboldauer den Wert 0 ergibt.
- Die so erzeugten Signale $s_{\rm I}(t)$ und $s_{\rm Q}(t)$ werden zusammengeführt, durch einen Digital–Analog–Wandler in ein zeitkontinuierliches Signal gewandelt und die bei der D/A–Wandlung erzeugten unerwünschten hochfrequenten Anteile vor dem Aussenden durch ein Tiefpassfilter (TP) eliminiert.
- Beim Empfänger wird das Signal $r(t)$ zunächst mittels A/D–Wandler in ein zeitdiskretes Signal gewandelt und anschließend werden über zwei Finite–Impulse–Response–Filter (FIR–Filter) und nachgelagerte Entscheider die Inphase– und Quadratur–Symbole $a_{\rm I}$ und $a_{\rm Q}$ extrahiert.
CAP war der de–facto–Standard bei den anfänglichen ADSL–Spezifikationen bis 1996. Die Frequenzen bis 4 kHz wurden für POTS reserviert. Der CAP–ADSL–Aufwärtskanal belegte den Frequenzbereich von 25 kHz bis 160 kHz und der Abwärtskanal die Frequenzen von 240 kHz bis 1.5 MHz. Die folgende Grafik zeigt das Referenzmodell.
Ein Problem bei CAP ist, dass ein „schlechter Kanal” dramatische Folgen auf die Übertragungsqualität hat. Deshalb findet man heute (2010) CAP–ADSL nur noch bei einigen wenigen HDSL–Varianten.
Grundlagen von DMT – Discrete Multitone Transmission
Discrete Multitone Transmission (DMT) bezeichnet ein Mehrträgermodulationsverfahren, das nahezu identisch mit Orthogonal Frequency Division Multiplexing (OFDM) ist. Bei leitungsgebundener Übertragung spricht man meist von „DMT”, bei drahtloser Übertragung von „OFDM”.
In beiden Fällen unterteilt man die gesamte Bandbreite in eine große Anzahl schmalbandiger äquidistanter Subkanäle. Die jeweiligen Subträgersignale $s_k(t)$ werden individuell mit komplexen Datensymbolen $D_k$ beaufschlagt und die Summe der modulierten Subträgersignale wird als Sendesignal $s(t)$ übertragen.
Die Grafik verdeutlicht das Prinzip von OFDM und DMT im Frequenzbereich, wobei teilweise die für ADSL/DMT spezifizierten Werte verwendet sind:
- 255 Subträger mit den Trägerfrequenzen $k · f_0$ ( $k$ = 1, ... , 255 ),
- Grundfrequenz $f_0$ = 4.3125 kHz, da 4000 Datenrahmen pro Sekunde übertragen werden, nach 68 Datenrahmen ein Synchronisationsrahmen eingefügt wird und aufgrund des zyklischen Präfix (siehe Kapitel 2.4) die Symboldauer $T = 1/f_0$ noch um den Faktor 16/17 verkürzt werden muss.
Ein wesentlicher Unterschied zwischen OFDM und DMT besteht darin, dass
- bei OFDM das dargestellte Spektrum $S(f)$ in Wirklichkeit ein äquivalentes Tiefpass-Spektrum $S_{\rm TP}(f)$ beschreibt und noch die Verschiebung um eine Trägerfrequenz $f_{\rm T}$ zu berücksichtigen ist:
- bei DMT dagegen noch die Anteile bei negativen Frequenzen berücksichtigt werden müssen, die mit den konjugiert–komplexen Spektralkoeffizienten zu gewichten sind:
Nach den Gleichungen der letzten Seite besteht das komplexe OFDM–Signal $s_{\rm OFDM}(t)$ aus $K$ = 255 komplexen Exponentialschwingungen. Das DMT–Signal $s_{\rm DMT}(t)$ setzt sich aus ebenso vielen Cosinusschwingungen mit Frequenzen $k · f_0$ zusammen (volle Belegung voausgesetzt). Trotz komplexer Koeffizienten $D_k$, die sich bei QAM–Belegung der Träger ergeben, ist das DMT–Signal wegen der konjugiert–komplexen Ergänzungen bei negativen Frequenzen stets reell.
Sowohl bei OFDM als auch bei der DMT ist allerdings das Sendesignal $s(t)$ zeitlich genau auf die Symboldauer $T = 1/f_0 ≈ 232 {\rm μs}$ begrenzt, was mathematisch der Multiplikation mit einem Rechteck der Dauer $T$ bedeutet. Im Spektralbereich entspricht dies der Faltung mit einer Spaltfunktion $\text{si}(πfT)$:
- Aus jeder Diracfunktion bei $k · f_0$ wird somit bei Berücksichtigung der zeitlichen Begrenzung eine si–Funktion an gleicher Stelle, wie im unteren Diagramm dargestellt.
- Benachbarte Subträgerspektren überlappen sich zwar auf der Frequenzachse, aber bei $k · f_0$ sind wieder die Koeffizienten $D_k$ zu erkennen, da alle anderen Spektren hier Nullstellen aufweisen.
- Für die untere Grafik ist ein symmetrisches Rechteck angenommen. Ein Rechteck zwischen 0 und $T$ hätte noch einen Phasenterm zur Folge. Es würde sich aber nichts bezüglich $|S(f)|$ ändern.
Geht man von den für den ADSL–Downstream günstigen Voraussetzungen aus, nämlich dass
- pro Sekunde 4000 Rahmen übertragen werden,
- stets alle Subträger aktiv sind ( $K$ = 255 ),
- jeder Träger mit einer 1024–QAM ( $b$ = 10, laut ITU 8 ≤ $b$ ≤ 15 ) belegt ist, und
- ideale Bedingungen herrschen, so dass die in der Grafik erkennbare Orthogonalität erhalten bleibt,
so ergibt sich für die maximale Daten(bit)rate $R_{\rm B,max}$ = 4000 · $K$ · $b$ ≈ 10 Mbit/s. Spezifiziert ist der ADSL–Downstream allerdings nur mit 2 Mbit/s (Aussparung der 64 untersten Träger wegen ISDN und Upstream, QAM–Belegung der stark gedämpften Träger mit weniger als 10 Bit, Berücksichtigung des zyklischen Präfix sowie einige betriebsbedingte Gründe).
DMT–Realisierung mit IDFT/DFT
Die folgende Grafik zeigt das DMT–Gesamtsystem, wobei wir uns zunächst auf die beiden roten Blöcke konzentrieren. Die blauen Blöcke werden im Kapitel 2.4 behandelt.
In vereinfachter Form lassen sich Sender und Empfänger wie in der unteren Grafik darstellen:
- Zur Durchführung der DMT–Modulation wird beim Sender ein Block an Eingangsbits in einem Datenpuffer angesammelt, der als ein Rahmen übertragen werden soll.
- Der QAM–Coder liefert pro Rahmen die komplexwertigen Datensymbole $D_1, ... , D_{255}$, die mit $D_0 = D_{256} = 0$ sowie $D_k = D_{512}–k∗ (k = 257, ... , 511)$ zum Vektor $\mathbf{D}$ der Länge 512 erweitert wird. Als Konsequenz finiter Signale sind $D_{257}, ... , D_{511}$ identisch mit $D_{–255}, ... , D_{–1}$.
- Die Spektralabtastwerte $\mathbf{D}$ werden mittels der Inversen Diskreten Fouriertransformation (IDFT) in den Vektor $\mathbf{s}$ der Zeitsignalabtastwerte umgerechnet, ebenfalls mit Länge 512. Wegen der konjugiert–komplexen Belegung im Spektralbereich ist $\text{Im}\{\mathbf{s}\}$ = 0.
- Nach Parallel/Seriell– und Digital/Analog–Wandlung und Tiefpassfilterung von $\text{Re}\{\mathbf{s}\}$ ergibt sich das physikalische und damit reelle sowie zeitkontinuierliche Sendesignal $s(t)$. Für dieses gilt im Bereich 0 ≤ $t$ ≤ $T$ (Faktor 2, da jeweils zwei Koeffizienten zu Cosinus/Sinus beitragen):
- Das Empfangssignal bei Übertragung über den AWGN–Kanal ist $r(t) = s(t) + n(t)$. Nach A/D– und S/P–Wandlung kann $r(t)$ durch den (reellen) Vektor $\mathbf{r}$ ausgedrückt werden. Die Diskrete Fouriertransformation (DFT) liefert dann Schätzwerte für die gesendeten Spektralkoeffizienten.
Betrachten wir als Beispiel den ADSL/DMT–Downstream. In der linken Grafik erkennt man die Beträge $|D_k|$ der belegten Subkanäle 64, ... , 255. Die Träger 0, ... , 63 für den reservierten Frequenzbereich von ISDN und Upstream sind auf 0 gesetzt. Rechts daneben sind die Spektralkoeffizienten $D_{64}, ... , D_{255}$ in der komplexen Zahlenebene dargestellt, wobei der Signalraum sehr groß gewählt ist.
Die untere Grafik zeigt das Sendesignal $s(t)$ für die Rahmendauer $T$ = $\frac{1}{f_0}$ ≈ 232 μs, das sich durch TP–Filterung der IDFT–Werte $s_0, ... , s_{511}$ ergibt. Dieses Nutzsignal sieht nahezu aus wie Rauschen.
Das Hauptproblem des DMT–Verfahrens ist der ungünstige Crestfaktor ⇒ Verhältnis von Maximalwert $s_{\rm max}$ und dem Effektivwert $s_{\rm eff}$ (Wurzel aus der mittleren Leistung) an. Der im beispielhaften Signalverlauf erkennbare große Dynamikbereich stellt hohe Anforderungen an die Linearität der Verstärker. Bei Begrenzung des Aussteuerbereichs werden die Spitzen von $s(t)$ abgeschnitten, was wie eine Impulsstörung wirkt und eine zusätzliche Rauschbelastung für das System darstellt.
Zusammenfassend lässt sich sagen:
- DMT ist im Prinzip die parallele Realisierung vieler schmalbandiger QAM–Modems mit unterschiedlichen Trägern und verhältnismäßig geringen Datenübertragungsraten.
- Die geringe Bandbreite pro Subträger ermöglicht eine lange Symboldauer, vermindert somit den Einfluss von Intersymbolinterferenzen und verringert den Entwicklungsaufwands für Entzerrer.
- Ein wesentlicher Grund für den Erfolg von DMT ist die technisch einfache Realisierung. IDFT und DFT werden mit digitalen Signalprozessoren (DSP) in Echtzeit gebildet.
- Da die Vektoren die Länge 512 (Zweierpotenz) besitzen, kann hierfür der besonders schnelle FFT–Algorithmus (Fast Fourier Transformation) angewendet werden.
Aufgaben zu Kapitel 2.3
Aufgabe 2.3: QAM–Signalraumbelegung
Zusatzaufgabe 2.3Z: xDSL–Frequenzband
Aufgabe 2.4: DSL/DMT_mit_IDFT/DFT
Zusatzaufgabe 2.4Z: Wiederholung_zur_IDFT