Difference between revisions of "Applets:Binomial and Poisson Distribution (Applet)"
| Line 157: | Line 157: | ||
*In order to average the same number of "ones" as the Binomial distribution during the period $T_{\rm I}$ (in the example: six), the characteristic probability $p = {\rm Pr}( e_i = 1)$ to the infinitesimal small time interval $T$ must go to zero | *In order to average the same number of "ones" as the Binomial distribution during the period $T_{\rm I}$ (in the example: six), the characteristic probability $p = {\rm Pr}( e_i = 1)$ to the infinitesimal small time interval $T$ must go to zero | ||
| − | == | + | ==Exercises== |
<br> | <br> | ||
| − | + | The terms used in the description are | |
| − | * | + | *Blue: Distribution function 1 (marked blue in applet) |
| − | * | + | *Red: Distribution function 2 (marked red in applet) |
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | '''(1)''' | + | '''(1)''' Set '''Blue''' to: Binomial distribution $(I=5, \ p=0.4)$ and '''Red''' to: Binomial distribution $(I=10, \ p=0.2)$. |
| − | : | + | :What are the probabilities ${\rm Pr}(z=0)$ and ${\rm Pr}(z=1)$?}} |
| − | $\hspace{1.0cm}\Rightarrow\hspace{0.3cm}\text{ | + | $\hspace{1.0cm}\Rightarrow\hspace{0.3cm}\text{Blue: }{\rm Pr}(z=0)=0.6^5=7.78\%, \hspace{0.3cm}{\rm Pr}(z=1)=0.4 \cdot 0.6^4=25.92\%;$ |
| − | $\hspace{1.85cm}\text{ | + | $\hspace{1.85cm}\text{Red: }{\rm Pr}(z=0)=0.8^10=10.74\%, \hspace{0.3cm}{\rm Pr}(z=1)=0.2 \cdot 0.8^9=26.84\%.$ |
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | '''(2)''' | + | '''(2)''' Using the same settings as '''(1)''', what are the probabilities ${\rm Pr}(3 \le z \le 5)$?}} |
| − | $\hspace{1.0cm}\Rightarrow\hspace{0.3cm}\text{ | + | $\hspace{1.0cm}\Rightarrow\hspace{0.3cm}\text{Formular: }{\rm Pr}(3 \le z \le 5) = {\rm Pr}(z=3) + {\rm Pr}(z=4) + {\rm Pr}(z=5)\text{, or } |
{\rm Pr}(3 \le z \le 5) = {\rm Pr}(z \le 5) - {\rm Pr}(z \le 2)$ | {\rm Pr}(3 \le z \le 5) = {\rm Pr}(z \le 5) - {\rm Pr}(z \le 2)$ | ||
| − | $\hspace{1.85cm}\text{ | + | $\hspace{1.85cm}\text{Blue: }{\rm Pr}(3 \le z \le 5) = 0.2304+ 0.0768 + 0.0102 =1 - 0.6826 = 0.3174;$ |
| − | $\hspace{1.85cm}\text{ | + | $\hspace{1.85cm}\text{Red: }{\rm Pr}(3 \le z \le 5) = 0.2013 + 0.0881 + 0.0264 = 0.9936 - 0.6778 = 0.3158$ |
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | '''(3)''' | + | '''(3)''' Using the same settings as '''(1)'''. what are the differences in the mean $m_1$ und die Streuung $\sigma$ der beiden Binomialverteilungen?}} |
| Line 218: | Line 218: | ||
$\hspace{1.85cm}\text{Die Poissonverteilung wird dagegen nie symmetrisch, da sie sich bis ins Unendliche erstreckt!}$ | $\hspace{1.85cm}\text{Die Poissonverteilung wird dagegen nie symmetrisch, da sie sich bis ins Unendliche erstreckt!}$ | ||
| − | |||
==Über die Autoren== | ==Über die Autoren== | ||
Revision as of 16:07, 23 February 2018
Contents
Applet Description
This applet allows the calculation and graphic display of
- the probabilities ${\rm Pr}(z=\mu)$ of a discrete random variable $z \in \{\mu \} = \{0, 1, 2, 3, \text{...} \}$, that determine its Probability Density Function (PDF) (graphic representation with Dirac functions ${\rm \delta}( z-\mu)$):
- $$f_{z}(z)=\sum_{\mu=1}^{M}{\rm Pr}(z=\mu)\cdot {\rm \delta}( z-\mu),$$
- the probabilities ${\rm Pr}(z \le \mu)$ of the Cumulative Distribution Function (CDF) $F_{z}(\mu)={\rm Pr}(z\le\mu)$.
Discrete distributions are available in two sets of parameters:
- the Binomial distribution with the parameters $I$ and $p$ ⇒ $z \in \{0, 1, \text{...} \ , I \}$ ⇒ $M = I+1$ possible values,
- the Poisson distribution with the parameter $\lambda$ ⇒ $z \in \{0, 1, 2, 3, \text{...}\}$ ⇒ $M \to \infty$.
At the exercises below you are to compare:
- two Binomial distributions with different sets of parameters $I$ and $p$,
- two Poisson distributions with different rates $\lambda$,
- a Binomial distribution with a Poisson distribution.
Theoretical Background
Properties of Binomial Distribution
The Binomial distribution represents an important special case for the likelihood of occurence of a discrete random variable. For the derivation we assume, that $I$ binary and statistically independent random variables $b_i \in \{0, 1 \}$ can take
- the value $1$ with the probability ${\rm Pr}(b_i = 1) = p$, and
- the value $0$ with the probability ${\rm Pr}(b_i = 0) = 1-p$.
Then the sum $z$, which is also a discrete random variable with the symbol stock $\{0, 1, 2, \text{...}\ , I\}$, is called binomially distributed:
- $$z=\sum_{i=1}^{I}b_i.$$
The symbol scope is thus $M = I + 1.$
Probabilities of binomial distribution
Following formular applies for $μ = 0, \text{...}\ , I$:
- $$p_\mu = {\rm Pr}(z=\mu)={I \choose \mu}\cdot p^\mu\cdot ({\rm 1}-p)^{I-\mu},$$
whereby the first term provides the number of combinations $(I \text{ over }\mu)$ :
- $${I \choose \mu}=\frac{I !}{\mu !\cdot (I-\mu) !}=\frac{ {I\cdot (I- 1) \cdot \ \cdots \ \cdot (I-\mu+ 1)} }{ 1\cdot 2\cdot \ \cdots \ \cdot \mu}.$$
Moments of Binomial Distribution
Following formular applies to a binomially distributed random variable of order $k$:
- $$m_k={\rm E}[z^k]=\sum_{\mu={\rm 0}}^{I}\mu^k\cdot{I \choose \mu}\cdot p^\mu\cdot ({\rm 1}-p)^{I-\mu}.$$
From it we can derive the formulars for:
- the linear average: $m_1 = I\cdot p,$
- the quadratic average: $m_2 = (I^2-I)\cdot p^2+I\cdot p,$
- the variance and dispersion: $\sigma^2 = {m_2-m_1^2} = {I \cdot p\cdot (1-p)} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} \sigma = \sqrt{I \cdot p\cdot (1-p)}.$
Applications of Binomial Distribution
The Binomial distribution has a variety of uses in telecommunications as well as other disciplines :
- It characterizes the distribution of rejected parts (Ausschussstücken) in the statistical quality control.
- The bit error rate of a digital transmission system gained through simulation is technically a binomially distributed random variable as well.
- The binomial distribution can be used to calculate the residual error probability with blockwise coding, as the following example shows.
$\text{Example 1:}$ When transfering blocks of $I =5$ binary symbols through a channel, that
- distorts a symbol with probability $p = 0.1$ ⇒ Random variable $e_i = 1$, and
- transfers the symbol undistorted with probability $1 - p = 0.9$ ⇒ Random variable $e_i = 0$,
the new random variable $f$ („Error per block”) calculates to:
- $$f=\sum_{i=1}^{I}e_i.$$
$f$ can now assume integer values between $\mu = 0$ (no symbol is distorted) and $\mu = I$ (all five symbols are distorted). We describe the probability of $\mu$ distortions as $p_μ = {\rm Pr}(f = \mu)$.
- The case that all five symbols are transmitted correctly occurs with the probability of $p_0 = 0.9^{5} ≈ 0.5905$. This also be concluded from the binomial formula for $μ = 0$ , taking into account the definition „10 over 0“ = 1.
- A singular error $(f = 1)$ occurs with the probability $p_1 = 5\cdot 0.1\cdot 0.9^4\approx 0.3281$. The first factor indicates, that there are $5\text{ über } 1 = 5$ possibilities to position the error. The other two factors take into account, that one symbol was distorted and the other four are intact, when $f =1$.
- For $f =2$ there are $5\text{ über } 2 = (5 \cdot 4)/(1 \cdot 2) = 10$ combinations and you get a probability of $p_2 = 10\cdot 0.1^2\cdot 0.9^3\approx 0.0729$.
If a block code can correct up to two errors, then the rest error probability is $p_{\rm R} = 1-p_{\rm 0}-p_{\rm 1}-p_{\rm 2}\approx 0.85\%$.
A second calculation option would be $p_{\rm R} = p_{3} + p_{4} + p_{5}$ with the approximation $p_{\rm R} \approx p_{3} = 0.81\%.$
The mean number of errors in a block is $m_f = 5 \cdot 0.1 = 0.5$. The variance of the random variable $f$ is $\sigma_f^2 = 5 \cdot 0.1 \cdot 0.9= 0.45$ ⇒ $\sigma_f \approx 0.671.$
Properties of Poisson Distribution
The Poisson distribution is a special case of the Binomial distribution, where
- for one $I → ∞$ and $p →$ 0.
- Additionally, the product of $I · p = λ$ must be finite.
The parameter $λ$ indicates the average number of "ones" in a specified time unit and is called rate.
Unlike with the Binomial distribution ($0 ≤ μ ≤ I$), here, the random variable can assume arbitrarily large non-negative integers, which means that the number of possible valuess is not countable. However, since no intermediate values can occur, this too referred to as a "discrete distribution".
Probabilities of Poisson Distribution
Taking into account the abovementioned limit transitions in the equation for the probabilities of the binomial distribution, the likelihood of occurence of the Poisson distributed random variable $z$ can be calculated through:
- $$p_\mu = {\rm Pr} ( z=\mu ) = \lim_{I\to\infty} \cdot \frac{I !}{\mu ! \cdot (I-\mu )!} \cdot (\frac{\lambda}{I} )^\mu \cdot ( 1-\frac{\lambda}{I})^{I-\mu}.$$
After some algebraic transformations we obtain:
- $$p_\mu = \frac{ \lambda^\mu}{\mu!}\cdot {\rm e}^{-\lambda}.$$
Moments of Poisson Distribution
With the Poisson distribution, the average and the dispersion result directly from the corresponding equations of the binomial distribution through a twofold limit formation:
- $$m_1 =\lim_{\left.{I\hspace{0.05cm}\to\hspace{0.05cm}\infty \atop {p\hspace{0.05cm}\to\hspace{0.05cm} 0}}\right.} I \cdot p= \lambda,$$
- $$\sigma =\lim_{\left.{I\hspace{0.05cm}\to\hspace{0.05cm}\infty \atop {p\hspace{0.05cm}\to\hspace{0.05cm} 0}}\right.} \sqrt{I \cdot p \cdot (1-p)} = \sqrt {\lambda}.$$
We can see that with the Poisson distribution $\sigma^2 = m_1 = \lambda$ always holds. By contrast, $\sigma^2 < m_1$ always applies to the binomial distribution .
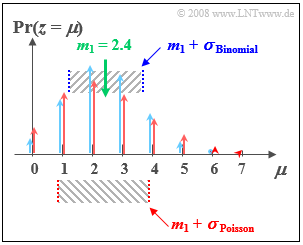
$\text{Example 2:}$ We now compare
- the Binomial distribution with parameters $I =6$ und $p = 0.4$ with
- the Poisson distribution with $λ = 2.4$:
- Both distributions have the same linear average $m_1 = 2.4$.
- The dispersion of the Poisson distribution (marked red in the picture) is $σ ≈ 1.55$.
- The standard deviation of the Binomial distribution (marked blue) is $σ = 1.2$.
Applications of Poisson Distribution
The Poisson distribution is the result of a so-called Poisson point process which is often used as a model for a series of events that may occur at random times. Examples of such events are
- the failure of devices - an important task in reliability theory,
- the shot noise in the optical transmission, and
- the start of conversations at a telephone exchange(„Teletraffic engineering”).
$\text{Example 3:}$ A telephone exchange receives ninety requests per minute on average ($λ = 1.5 \text{ per second}$). The probabilities $p_µ$, that in an arbitrarily large time frame exactly $\mu$ requests are received, is:
- $$p_\mu = \frac{1.5^\mu}{\mu!}\cdot {\rm e}^{-1.5}.$$
The resulting numerical values are $p_0 = 0.223$, $p_1 = 0.335$, $p_2 = 0.251$, etc.
From this, additional parameters can be derived:
- the distance $τ$ between two requests satisfies the "exponential distribution",
- The mean time span between two requests is ${\rm E}[τ] = 1/λ ≈ 0.667 \ \rm s$.
Comparison Binomial vs. Poisson Distribution
This segment deals with the similarities and differences between Binomial and Poisson distributions.
The Binomial distribution is used to describe stochastic events, that have a fixed period $T$. For example the period of an ISDN (Integrated Services Digital Network) with $64 \ \rm kbit/s$ is $T \approx 15.6 \ \rm µ s$.
- Binary events such as the error-free $(e_i = 0)$/ faulty $(e_i = 1)$ transmission of individual symbols only occur in this time frame.
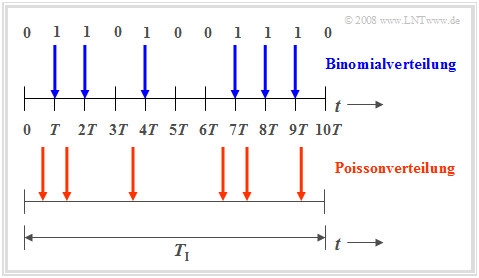
- The binomial distribution allows one to make statistical statements about the number of expected transmission erros in a period $T_{\rm I} = I · T$, as is shown in the time chart above(marked blue).
- For very large values of $I$ the Binomial distribution can be approximated by the Poisson distribution.
- if at the same time $I · p \gg 1$, then the Poisson distribution (as well as the Binomial distribution) turns into a discrete gaussian distribution according to the de Moivre-Laplace theorem.
The Poisson distribution can also be used to make statements about the number of occuring binary events in a finite time interval.
By assuming the same observation period $T_{\rm I}$ and increasing the number of partial periods $I$, the period $T$, in which a new event ($0$ or $1$) can occur, gets smaller and smaller. In the borderline case $T$ goes to zero. This means:
- With the Poisson distribution binary events can not only occur at certain given times, but at any time, which is illustrated in the time chart below.
- In order to average the same number of "ones" as the Binomial distribution during the period $T_{\rm I}$ (in the example: six), the characteristic probability $p = {\rm Pr}( e_i = 1)$ to the infinitesimal small time interval $T$ must go to zero
Exercises
The terms used in the description are
- Blue: Distribution function 1 (marked blue in applet)
- Red: Distribution function 2 (marked red in applet)
(1) Set Blue to: Binomial distribution $(I=5, \ p=0.4)$ and Red to: Binomial distribution $(I=10, \ p=0.2)$.
- What are the probabilities ${\rm Pr}(z=0)$ and ${\rm Pr}(z=1)$?
$\hspace{1.0cm}\Rightarrow\hspace{0.3cm}\text{Blue: }{\rm Pr}(z=0)=0.6^5=7.78\%, \hspace{0.3cm}{\rm Pr}(z=1)=0.4 \cdot 0.6^4=25.92\%;$
$\hspace{1.85cm}\text{Red: }{\rm Pr}(z=0)=0.8^10=10.74\%, \hspace{0.3cm}{\rm Pr}(z=1)=0.2 \cdot 0.8^9=26.84\%.$
(2) Using the same settings as (1), what are the probabilities ${\rm Pr}(3 \le z \le 5)$?
$\hspace{1.0cm}\Rightarrow\hspace{0.3cm}\text{Formular: }{\rm Pr}(3 \le z \le 5) = {\rm Pr}(z=3) + {\rm Pr}(z=4) + {\rm Pr}(z=5)\text{, or }
{\rm Pr}(3 \le z \le 5) = {\rm Pr}(z \le 5) - {\rm Pr}(z \le 2)$
$\hspace{1.85cm}\text{Blue: }{\rm Pr}(3 \le z \le 5) = 0.2304+ 0.0768 + 0.0102 =1 - 0.6826 = 0.3174;$
$\hspace{1.85cm}\text{Red: }{\rm Pr}(3 \le z \le 5) = 0.2013 + 0.0881 + 0.0264 = 0.9936 - 0.6778 = 0.3158$
(3) Using the same settings as (1). what are the differences in the mean $m_1$ und die Streuung $\sigma$ der beiden Binomialverteilungen?
$\hspace{1.0cm}\Rightarrow\hspace{0.3cm}\text{Mittelwert:}\hspace{0.2cm}m_\text{1} = I \cdot p\hspace{0.3cm} \Rightarrow\hspace{0.3cm} m_\text{1, Blau} = 5 \cdot 0.4\underline{ = 2 =} \ m_\text{1, Rot} = 10 \cdot 0.2; $
$\hspace{1.85cm}\text{Streuung:}\hspace{0.4cm}\sigma = \sqrt{I \cdot p \cdot (1-p)} = \sqrt{m_1 \cdot (1-p)}\hspace{0.3cm}\Rightarrow\hspace{0.3cm} \sigma_{\rm Blau} = \sqrt{2 \cdot 0.6} =1.095 \le \sigma_{\rm Rot} = \sqrt{2 \cdot 0.8} = 1.265.$
(4) Setzen Sie Blau: Binomialverteilung $(I=15, p=0.3)$ und Rot: Poissonverteilung $(\lambda=4.5)$.
- Welche Unterschiede ergeben sich zwischen beiden Verteilungen hinsichtlich Mittelwert $m_1$ und Varianz $\sigma^2$?
$\hspace{1.0cm}\Rightarrow\hspace{0.3cm}\text{Beide Verteilungern haben gleichen Mittelwert:}\hspace{0.2cm}m_\text{1, Blau} = I \cdot p\ = 15 \cdot 0.3\hspace{0.15cm}\underline{ = 4.5 =} \ m_\text{1, Rot} = \lambda$;
$\hspace{1.85cm} \text{Binomialverteilung: }\hspace{0.2cm} \sigma_\text{Blau}^2 = m_\text{1, Blau} \cdot (1-p)\hspace{0.15cm}\underline { = 3.15} \le \text{Poissonverteilung: }\hspace{0.2cm} \sigma_\text{Rot}^2 = \lambda\hspace{0.15cm}\underline { = 4.5}$;
(5) Es gelten die Einstellungen von (4). Wie groß sind die Wahrscheinlichkeiten ${\rm Pr}(z \gt 10)$ und ${\rm Pr}(z \gt 15)$
$\hspace{1.0cm}\Rightarrow\hspace{0.3cm} \text{Binomial: }\hspace{0.2cm} {\rm Pr}(z \gt 10) = 1 - {\rm Pr}(z \le 10) = 1 - 0.9993 = 0.0007;\hspace{0.3cm} {\rm Pr}(z \gt 15) = 0$.
$\hspace{1.85cm}\text{Poisson: }\hspace{0.2cm} {\rm Pr}(z \gt 10) = 1 - 0.9933 = 0.0067;\hspace{0.3cm}{\rm Pr}(z \gt 15) \gt 0\hspace{0.5cm}\text{Näherung: }\hspace{0.2cm}{\rm Pr}(z \gt 15) \ge {\rm Pr}(z = 16) = \frac{\lambda^{16} }{16!}\approx 2 \cdot 10^{-22}$
(6) Es gelten weiter die Einstellungen von (4). Mit welchen Parametern ergeben sich symmetrische Verteilungen um $m_1$?
$\hspace{1.0cm}\Rightarrow\hspace{0.3cm} \text{Binomialverung mit }p = 0.5\text{: }p_\mu = {\rm Pr}(z = \mu)\text{ symmetrisch um } m_1 = I/2 = 7.5 \ ⇒ \ p_μ = p_{I–μ}\ ⇒ \ p_8 = p_7, \ p_9 = p_6, \text{usw.}$
$\hspace{1.85cm}\text{Die Poissonverteilung wird dagegen nie symmetrisch, da sie sich bis ins Unendliche erstreckt!}$
Über die Autoren
Dieses interaktive Berechnungstool wurde am Lehrstuhl für Nachrichtentechnik der Technischen Universität München konzipiert und realisiert.
- Die erste Version wurde 2003 von Ji Li im Rahmen ihrer Diplomarbeit mit „FlashMX–Actionscript” erstellt (Betreuer: Günter Söder).
- 2018 wurde dieses Programm von Jimmy He im Rahmen seiner Bachelorarbeit (Betreuer: Tasnád Kernetzky – Mitarbeiter der Professur „Leitungsgebundene Übertragungstechnik„) auf „HTML5” umgesetzt und neu gestaltet.