Difference between revisions of "Applets:Complementary Gaussian Error Functions"
| Line 22: | Line 22: | ||
==Theoretischer Hintergrund== | ==Theoretischer Hintergrund== | ||
| + | <br> | ||
| + | Bei der Untersuchung digitaler Übertragungssysteme muss oft die Wahrscheinlichkeit bestimmt werden, dass eine (mittelwertfreie) gaußverteilte Zufallsgröße $x$ mit der Varianz $σ^2$ einen vorgegebenen Wert $x_0$ überschreitet. Für diese Wahrscheinlichkeit gilt: | ||
| + | :$${\rm Pr}(x > x_{\rm 0})={\rm Q}(\frac{x_0}{\sigma}) = 0.5 \cdot {\rm erfc}(\frac{x_0}{\sqrt{2} \cdot \sigma}).$$ | ||
| + | ===Die Q–Funktion=== | ||
| + | Die Funktion ${\rm Q}(x)$ bezeichnet man als das ''Komplementäre Gaußsche Fehlerintegral''. Es gilt folgende Berechnungsvorschrift: | ||
| + | :$$\rm Q (\it x\rm ) = \frac{\rm 1}{\sqrt{\rm 2\pi}}\int_{\it x}^{\rm +\infty}\hspace{-0.2cm}\rm e^{\it -u^{\rm 2}/\hspace{0.05cm} \rm 2}\,d \it u .$$ | ||
| + | *Dieses Integral ist nicht analytisch lösbar und muss – wenn man dieses Applet nicht zur Verfügung hat – aus Tabellen entnommen werden. | ||
| + | *Speziell für größere $x$–Werte von (also für kleine Fehlerwahrscheinlichkeiten) liefern die nachfolgend angegebenen Schranken eine brauchbare Abschätzung für das Komplementäre Gaußsche Fehlerintegral. ${\rm Q}_o(x)$ bezeichnet hierbei eine obere und ${\rm Q}_u(x)$ eine untere Schranke: | ||
| + | :$${\rm Q_o}(x )=\frac{ 1}{\sqrt{2\pi}\cdot x}\cdot {\rm e}^{- x^{2}/\hspace{0.05cm}2} > {\rm Q}(x), $$ | ||
| + | :$${\rm Q_u}(x )=\frac{\rm 1-{\rm 1}/{\it x^{\rm 2}}}{\sqrt{\rm 2\pi}\cdot \it x}\cdot \rm e^{-\it x^{\rm 2}/\hspace{0.05cm}\rm 2} =\rm Q_0(\it x \rm )\left(\rm 1-{\rm 1}/{\it x^{\rm 2}}\right)< {\rm Q}(x), .$$ | ||
| + | ===Die Funktion erfc(''x'')=== | ||
| + | |||
| + | In Bibliotheken findet man oft die Funktion | ||
| + | :$${\rm erfc}(x),$$ | ||
| + | die mit ${\rm Q}(x)$ wie folgt zusammenhängt: | ||
| + | :$$\rm Q(\it x\rm )={\rm 1}/\hspace{0.05cm}{\rm 2}\cdot \rm erfc({\it x}/{\sqrt{\rm 2}}).$$ | ||
| + | |||
| + | Das Grafik zeigt die Q-Funktion in logarithmischer Darstellung für lineare (obere Achse) und logarithmische Abszissenwerte (untere Achse). | ||
| + | *Die obere Schranke (rote Kreise) ist ab ca. $x = 1$ brauchbar, die untere Schranke (grüne Rauten) ab $x ≈ 2$. | ||
| + | *Für $x ≥ 4$ sind beide Schranken innerhalb der Zeichengenauigkeit vom tatsächlichen Verlauf ${\rm Q}(x)$ nicht mehr zu unterscheiden. | ||
==Zur Handhabung des Applets== | ==Zur Handhabung des Applets== | ||
Revision as of 18:09, 7 March 2018
Contents
Programmbeschreibung
Dieses Applet ermöglicht die Berechnung und graphische Darstellung
- der Wahrscheinlichkeiten ${\rm Pr}(z=\mu)$ einer diskreten Zufallsgröße $z \in \{\mu \} = \{0, 1, 2, 3, \text{...} \}$, welche die Wahrscheinlichkeitsdichtefunktion (WDF) – im Englischen Probability Density Function (PDF) – der Zufallsgröße $z$ bestimmen – hier Darstellung mit Diracfunktionen ${\rm \delta}( z-\mu)$:
- $$f_{z}(z)=\sum_{\mu=1}^{M}{\rm Pr}(z=\mu)\cdot {\rm \delta}( z-\mu),$$
- der Wahrscheinlichkeiten ${\rm Pr}(z \le \mu)$ der Verteilungsfunktion (VTF) – im Englischen Cumulative Distribution Function (CDF):
- $$F_{z}(\mu)={\rm Pr}(z\le\mu).$$
Als diskrete Verteilungen stehen in zwei Parametersätzen zur Auswahl:
- die Binomialverteilung mit den Parametern $I$ und $p$ ⇒ $z \in \{0, 1, \text{...} \ , I \}$ ⇒ $M = I+1$ mögliche Werte,
- die Poissonverteilung mit Parameter $\lambda$ ⇒ $z \in \{0, 1, 2, 3, \text{...}\}$ ⇒ $M \to \infty$.
In der Versuchsdurchführung sollen Sie miteinander vergleichen:
- je zwei Binomialverteilungen mit unterschiedlichen Parameterwerten $I$ und $p$,
- je zwei Poissonverteilungen mit unterschiedlicher Rate $\lambda$,
- jeweils eine Binomial– und eine Poissonverteilung.
Theoretischer Hintergrund
Bei der Untersuchung digitaler Übertragungssysteme muss oft die Wahrscheinlichkeit bestimmt werden, dass eine (mittelwertfreie) gaußverteilte Zufallsgröße $x$ mit der Varianz $σ^2$ einen vorgegebenen Wert $x_0$ überschreitet. Für diese Wahrscheinlichkeit gilt:
- $${\rm Pr}(x > x_{\rm 0})={\rm Q}(\frac{x_0}{\sigma}) = 0.5 \cdot {\rm erfc}(\frac{x_0}{\sqrt{2} \cdot \sigma}).$$
Die Q–Funktion
Die Funktion ${\rm Q}(x)$ bezeichnet man als das Komplementäre Gaußsche Fehlerintegral. Es gilt folgende Berechnungsvorschrift:
- $$\rm Q (\it x\rm ) = \frac{\rm 1}{\sqrt{\rm 2\pi}}\int_{\it x}^{\rm +\infty}\hspace{-0.2cm}\rm e^{\it -u^{\rm 2}/\hspace{0.05cm} \rm 2}\,d \it u .$$
- Dieses Integral ist nicht analytisch lösbar und muss – wenn man dieses Applet nicht zur Verfügung hat – aus Tabellen entnommen werden.
- Speziell für größere $x$–Werte von (also für kleine Fehlerwahrscheinlichkeiten) liefern die nachfolgend angegebenen Schranken eine brauchbare Abschätzung für das Komplementäre Gaußsche Fehlerintegral. ${\rm Q}_o(x)$ bezeichnet hierbei eine obere und ${\rm Q}_u(x)$ eine untere Schranke:
- $${\rm Q_o}(x )=\frac{ 1}{\sqrt{2\pi}\cdot x}\cdot {\rm e}^{- x^{2}/\hspace{0.05cm}2} > {\rm Q}(x), $$
- $${\rm Q_u}(x )=\frac{\rm 1-{\rm 1}/{\it x^{\rm 2}}}{\sqrt{\rm 2\pi}\cdot \it x}\cdot \rm e^{-\it x^{\rm 2}/\hspace{0.05cm}\rm 2} =\rm Q_0(\it x \rm )\left(\rm 1-{\rm 1}/{\it x^{\rm 2}}\right)< {\rm Q}(x), .$$
Die Funktion erfc(x)
In Bibliotheken findet man oft die Funktion
- $${\rm erfc}(x),$$
die mit ${\rm Q}(x)$ wie folgt zusammenhängt:
- $$\rm Q(\it x\rm )={\rm 1}/\hspace{0.05cm}{\rm 2}\cdot \rm erfc({\it x}/{\sqrt{\rm 2}}).$$
Das Grafik zeigt die Q-Funktion in logarithmischer Darstellung für lineare (obere Achse) und logarithmische Abszissenwerte (untere Achse).
- Die obere Schranke (rote Kreise) ist ab ca. $x = 1$ brauchbar, die untere Schranke (grüne Rauten) ab $x ≈ 2$.
- Für $x ≥ 4$ sind beide Schranken innerhalb der Zeichengenauigkeit vom tatsächlichen Verlauf ${\rm Q}(x)$ nicht mehr zu unterscheiden.
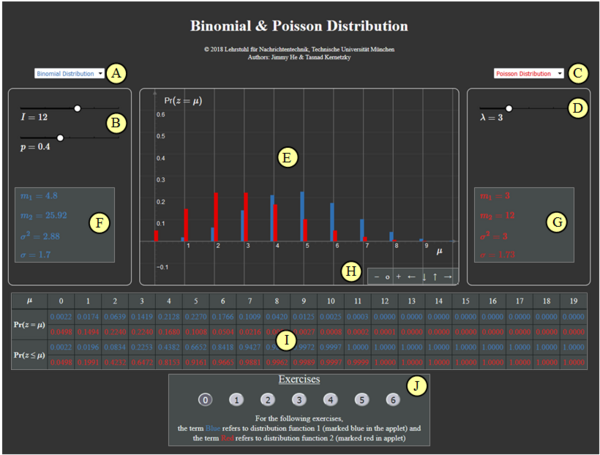
Zur Handhabung des Applets
(A) Vorauswahl für blauen Parametersatz
(B) Parametereingabe $I$ und $p$ per Slider
(C) Vorauswahl für roten Parametersatz
(D) Parametereingabe $\lambda$ per Slider
(E) Graphische Darstellung der Verteilungen
(F) Momentenausgabe für blauen Parametersatz
(G) Momentenausgabe für roten Parametersatz
(H) Variation der grafischen Darstellung
$\hspace{1.5cm}$„$+$” (Vergrößern),
$\hspace{1.5cm}$ „$-$” (Verkleinern)
$\hspace{1.5cm}$ „$\rm o$” (Zurücksetzen)
$\hspace{1.5cm}$ „$\leftarrow$” (Verschieben nach links), usw.
( I ) Ausgabe von ${\rm Pr} (z = \mu)$ und ${\rm Pr} (z \le \mu)$
(J) Bereich für die Versuchsdurchführung
Andere Möglichkeiten zur Variation der grafischen Darstellung:
- Gedrückte Shifttaste und Scrollen: Zoomen im Koordinatensystem,
- Gedrückte Shifttaste und linke Maustaste: Verschieben des Koordinatensystems.
Über die Autoren
Dieses interaktive Berechnungstool wurde am Lehrstuhl für Nachrichtentechnik der Technischen Universität München konzipiert und realisiert.
- Die erste Version wurde 2003 von Ji Li im Rahmen ihrer Diplomarbeit mit „FlashMX–Actionscript” erstellt (Betreuer: Günter Söder).
- 2018 wurde das Programm von Jimmy He (Bachelorarbeit, Betreuer: Tasnád Kernetzky ) auf „HTML5” umgesetzt und neu gestaltet.