Difference between revisions of "Theory of Stochastic Signals/Stochastic System Theory"
| Line 7: | Line 7: | ||
== # ÜBERBLICK ZUM FÜNFTEN HAUPTKAPITEL # == | == # ÜBERBLICK ZUM FÜNFTEN HAUPTKAPITEL # == | ||
| + | <br> | ||
| + | Dieses Kapitel beschreibt den Einfluss eines Filters auf die Autokorrelationsfunktion (AKF) und das Leistungsdichtespektrum (LDS) stochastischer Signalen. Im Einzelnen werden behandelt: | ||
| − | + | *die Berechnung von AKF und LDS am Filterausgang (''Stochastische Systemtheorie''), | |
| + | *die Struktur und die Darstellung ''Digitaler Filter'' (nichrekursiv und rekursiv), | ||
| + | *die ''Dimensionierung'' der Filterkoeffizienten für eine vorgegebene AKF, | ||
| + | *die Bedeutung des ''Matched-Filters'' für Nachrichtensysteme (SNR-Maximierung), | ||
| + | *die Eigenschaften des ''Wiener-Kolmogorow-Filters'' zur Signalrekonstruktion. | ||
| + | |||
| + | |||
| + | Weitere Informationen zum Thema „Filterung stochastischer Signale” sowie Aufgaben, Simulationen und Programmierübungen finden Sie im | ||
*Kapitel 10: Filterung stochastischer Signale (Programm fil) | *Kapitel 10: Filterung stochastischer Signale (Programm fil) | ||
*Kapitel 11: Optimale Filter (Programm ofi) | *Kapitel 11: Optimale Filter (Programm ofi) | ||
| + | |||
des Praktikums „Simulationsmethoden in der Nachrichtentechnik”. Diese (ehemalige) LNT-Lehrveranstaltung an der TU München basiert auf | des Praktikums „Simulationsmethoden in der Nachrichtentechnik”. Diese (ehemalige) LNT-Lehrveranstaltung an der TU München basiert auf | ||
| Line 18: | Line 28: | ||
*der [http://en.lntwww.de/downloads/Sonstiges/Texte/Praktikum_LNTsim_Teil_B.pdf Praktikumsanleitung - Teil B] ⇒ Link verweist auf die PDF-Version mit Kapitel 10: Seite 229-248 und Kapitel 11: Seite 249-270. | *der [http://en.lntwww.de/downloads/Sonstiges/Texte/Praktikum_LNTsim_Teil_B.pdf Praktikumsanleitung - Teil B] ⇒ Link verweist auf die PDF-Version mit Kapitel 10: Seite 229-248 und Kapitel 11: Seite 249-270. | ||
| − | |||
| − | |||
==Problemstellung== | ==Problemstellung== | ||
| + | <br> | ||
[[File:Sto_T_5_1_S1_version2.png |right| 300px|frame|Filtereinfluss auf Spektrum und LDS]] | [[File:Sto_T_5_1_S1_version2.png |right| 300px|frame|Filtereinfluss auf Spektrum und LDS]] | ||
Wir betrachten wie im Buch [[Lineare zeitinvariante Systeme]] die rechts skizzierte Anordnung, wobei das System | Wir betrachten wie im Buch [[Lineare zeitinvariante Systeme]] die rechts skizzierte Anordnung, wobei das System | ||
*sowohl durch die Impulsantwort $h(t)$ | *sowohl durch die Impulsantwort $h(t)$ | ||
*als auch durch seinen Frequenzgang $H(f)$ | *als auch durch seinen Frequenzgang $H(f)$ | ||
| − | eindeutig beschrieben ist. Der Zusammenhang zwischen diesen Beschreibungsgrößen im Zeit | + | |
| + | |||
| + | eindeutig beschrieben ist. Der Zusammenhang zwischen diesen Beschreibungsgrößen im Zeit– und Frequenzbereich ist durch die [[Signaldarstellung/Fouriertransformation_und_-rücktransformation#Eigenschaften_aperiodischer_Signale|Fouriertransformation]] gegeben. | ||
Legt man an den Eingang das Signal $x(t)$ an und bezeichnet das Ausgangssignal mit $y(t)$, so liefert die klassische Systemtheorie folgende Aussagen: | Legt man an den Eingang das Signal $x(t)$ an und bezeichnet das Ausgangssignal mit $y(t)$, so liefert die klassische Systemtheorie folgende Aussagen: | ||
| − | *Das Ausgangssignal $y(t)$ ergibt sich aus der Faltung zwischen dem Eingangssignal $x(t)$ und der Impulsantwort $h(t)$: | + | *Das Ausgangssignal $y(t)$ ergibt sich aus der [[Signaldarstellung/Faltungssatz_und_Faltungsoperation|Faltung]] zwischen dem Eingangssignal $x(t)$ und der Impulsantwort $h(t)$: |
:$$y(t) = x(t) \ast h(t) = \int_{-\infty}^{+\infty} x(\tau)\cdot h ( t - \tau) \,\,{\rm d}\tau.$$ | :$$y(t) = x(t) \ast h(t) = \int_{-\infty}^{+\infty} x(\tau)\cdot h ( t - \tau) \,\,{\rm d}\tau.$$ | ||
:Diese Gleichung gilt für deterministische und stochastische Signale gleichermaßen. | :Diese Gleichung gilt für deterministische und stochastische Signale gleichermaßen. | ||
| − | *Bei deterministischen Signalen geht man meist den Umweg über die Spektralfunktionen. Das | + | *Bei deterministischen Signalen geht man meist den Umweg über die Spektralfunktionen. Das Spektrum $X(f)$ ist die Fouriertransformierte von $x(t)$. Die Multiplikation mit dem Frequenzgang $H(f)$ führt zum Ausgangsspektrum $Y(f)$. Darauslässt sich das Signal $y(t)$ durch die Fourierrücktransformation gewinnen. |
*Bei stochastischen Signalen versagt diese Vorgehensweise, da dann die Zeitfunktionen $x(t)$ und $y(t)$ nicht für alle Zeiten von $–∞$ bis $+∞$ vorhersagbar sind und somit die dazugehörigen Amplitudenspektren $X(f)$ und $Y(f)$ gar nicht existieren. In diesem Fall muss auf die im letzten Kapitel definierten [[Stochastische_Signaltheorie/Leistungsdichtespektrum_(LDS)|Leistungsdichtespektren]] übergegangen werden. | *Bei stochastischen Signalen versagt diese Vorgehensweise, da dann die Zeitfunktionen $x(t)$ und $y(t)$ nicht für alle Zeiten von $–∞$ bis $+∞$ vorhersagbar sind und somit die dazugehörigen Amplitudenspektren $X(f)$ und $Y(f)$ gar nicht existieren. In diesem Fall muss auf die im letzten Kapitel definierten [[Stochastische_Signaltheorie/Leistungsdichtespektrum_(LDS)|Leistungsdichtespektren]] übergegangen werden. | ||
==Amplituden- und Leistungsdichtespektrum== | ==Amplituden- und Leistungsdichtespektrum== | ||
| − | Wir betrachten | + | <br> |
| + | Wir betrachten einen ergodischen Zufallsprozess $\{x(t)\}$, dessen Autokorrelationsfunktion $φ_x(τ)$ als bekannt vorausgesetzt wird. Das Leistungsdichtespektrum ${\it Φ}_x(f)$ ist dann über die Fouriertransformation ebenfalls eindeutig bestimmt und es gelten die folgenden Aussagen: | ||
| + | :[[File:P_ID467__Sto_T_5_1_S2_neu.png|right| |frame| Zur AKF- und LDS-Berechnung eines Zufallssignals]] | ||
*Das Leistungsdichtespektrum ${\it Φ}_x(f)$ kann – ebenso wie die Autokorrelationsfunktion $φ_x(τ)$ – für jede einzelne Musterfunktion des stationären und ergodischen Zufallsprozesses $\{x(t)\}$ angegeben werden, auch wenn der spezifische Verlauf von $x(t)$ explizit nicht bekannt ist. | *Das Leistungsdichtespektrum ${\it Φ}_x(f)$ kann – ebenso wie die Autokorrelationsfunktion $φ_x(τ)$ – für jede einzelne Musterfunktion des stationären und ergodischen Zufallsprozesses $\{x(t)\}$ angegeben werden, auch wenn der spezifische Verlauf von $x(t)$ explizit nicht bekannt ist. | ||
*Das [[Signaldarstellung/Fouriertransformation_und_-rücktransformation#Das_erste_Fourierintegral|Amplitudenspektrum]] $X(f)$ ist dagegen undefiniert, da bei Kenntnis der Spektralfunktion $X(f)$ auch die gesamte Zeitfunktion $x(t)$ von $–∞$ bis $+∞$ über die Fourierrücktransformation bekannt sein müsste, was bei einem stochastischen Signal eindeutig nicht der Fall sein kann. | *Das [[Signaldarstellung/Fouriertransformation_und_-rücktransformation#Das_erste_Fourierintegral|Amplitudenspektrum]] $X(f)$ ist dagegen undefiniert, da bei Kenntnis der Spektralfunktion $X(f)$ auch die gesamte Zeitfunktion $x(t)$ von $–∞$ bis $+∞$ über die Fourierrücktransformation bekannt sein müsste, was bei einem stochastischen Signal eindeutig nicht der Fall sein kann. | ||
| − | *Ist entsprechend der | + | *Ist entsprechend der nebenstehenden Skizze ein Zeitausschnitt der endlichen Zeitdauer $T_{\rm M}$ bekannt, so kann für diesen natürlich wieder die Fouriertransformation angewandt werden. |
| − | |||
| − | {{ | + | {{BlaueBox|TEXT= |
| − | + | $\text{Satz:}$ | |
| − | :$${{\it \Phi}_x(f)} = \lim_{T_{\rm M}\to\infty}\hspace{0.2cm} | + | Zwischen dem Leistungsdichtespektrum ${\it Φ}_x(f)$ des unendlich ausgedehnten Zufallssignals $x(t)$ und dem Amplitudenspektrum $X_{\rm T}(f)$ des begrenzten Zeitausschnittes $x_{\rm T}(t)$ besteht der folgende Zusammenhang: |
| − | \frac{1}{ T_{\rm M}}\cdot | + | :$${ {\it \Phi}_x(f)} = \lim_{T_{\rm M}\to\infty}\hspace{0.2cm} |
| + | \frac{1}{ T_{\rm M} }\cdot \vert X_{\rm T}(f)\vert ^2.$$}} | ||
| − | + | {{BlaueBox|TEXT= | |
| + | $\text{Beweis:}$ | ||
| + | Vorne wurde die | ||
[[Stochastische_Signaltheorie/Autokorrelationsfunktion_(AKF)#Autokorrelationsfunktion_bei_ergodischen_Prozessen|Autokorrelationsfunktion]] eines ergodischen Prozesses mit der Musterfunktion $x(t)$ wie folgt angegeben: | [[Stochastische_Signaltheorie/Autokorrelationsfunktion_(AKF)#Autokorrelationsfunktion_bei_ergodischen_Prozessen|Autokorrelationsfunktion]] eines ergodischen Prozesses mit der Musterfunktion $x(t)$ wie folgt angegeben: | ||
| − | :$${{\it \varphi}_x(\tau)} = \lim_{T_{\rm M}\to\infty}\hspace{0.2cm} | + | :$${ {\it \varphi}_x(\tau)} = \lim_{T_{\rm M}\to\infty}\hspace{0.2cm} |
| − | \frac{1}{ T_{\rm M}}\cdot\int^{+T_{\rm M}/2}_{-T_{\rm | + | \frac{1}{ T_{\rm M} }\cdot\int^{+T_{\rm M}/2}_{-T_{\rm |
M}/2}x(t)\cdot x(t + \tau)\hspace{0.1cm} \rm d \it t.$$ | M}/2}x(t)\cdot x(t + \tau)\hspace{0.1cm} \rm d \it t.$$ | ||
| − | Es ist | + | Es ist zulässig, die zeitlich unbegrenzte Funktion $x(t)$ durch die auf den Zeitbereich $-T_{\rm M}/2$ bis $+T_{\rm M}/2$ begrenzte Funktion $x_{\rm T}(t)$ zu ersetzen. $x_{\rm T}(t)$ korrespondiert mit dem Spektrum $X_{\rm T}(f)$, und man erhält durch Anwendung des [[Signaldarstellung/Fouriertransformation_und_-rücktransformation#Das_erste_Fourierintegral|ersten Fourierintegrals]] und des [[Signaldarstellung/Gesetzmäßigkeiten_der_Fouriertransformation#Verschiebungssatz|Verschiebungssatzes]]: |
| − | :$${{\it \varphi}_x(\tau)} = \lim_{T_{\rm M}\to\infty}\hspace{0.2cm} | + | :$${ {\it \varphi}_x(\tau)} = \lim_{T_{\rm M}\to\infty}\hspace{0.2cm} |
| − | \frac{1}{ T_{\rm M}}\cdot \int^{+T_{\rm M}/2}_{-T_{\rm | + | \frac{1}{ T_{\rm M} }\cdot \int^{+T_{\rm M}/2}_{-T_{\rm |
M}/2}x_{\rm T}(t)\cdot \int^{+\infty}_{-\infty}X_{\rm | M}/2}x_{\rm T}(t)\cdot \int^{+\infty}_{-\infty}X_{\rm | ||
| − | T}(f)\cdot {\rm e}^{{\rm j}2 \pi f ( t + \tau) } \hspace{0.1cm} | + | T}(f)\cdot {\rm e}^{ {\rm j}2 \pi f ( t + \tau) } \hspace{0.1cm} |
\rm d \it f \hspace{0.1cm} \rm d \it t.$$ | \rm d \it f \hspace{0.1cm} \rm d \it t.$$ | ||
Nach Aufspalten des Exponenten und Vertauschen von Zeit- und Frequenzintegral ergibt sich: | Nach Aufspalten des Exponenten und Vertauschen von Zeit- und Frequenzintegral ergibt sich: | ||
| − | :$${{\it \varphi}_x(\tau)} = \lim_{T_{\rm M}\to\infty}\hspace{0.2cm} | + | :$${ {\it \varphi}_x(\tau)} = \lim_{T_{\rm M}\to\infty}\hspace{0.2cm} |
| − | \frac{1}{ T_{\rm M}}\cdot \int^{+\infty}_{-\infty}X_{\rm | + | \frac{1}{ T_{\rm M} }\cdot \int^{+\infty}_{-\infty}X_{\rm |
T}(f)\cdot \left[ \int^{+T_{\rm M}/2}_{-T_{\rm M}/2}x_{\rm | T}(f)\cdot \left[ \int^{+T_{\rm M}/2}_{-T_{\rm M}/2}x_{\rm | ||
| − | T}(t)\cdot {\rm e}^{{\rm j}2 \pi f t } \hspace{0.1cm} \rm d \it | + | T}(t)\cdot {\rm e}^{ {\rm j}2 \pi f t } \hspace{0.1cm} \rm d \it |
| − | t \right] \cdot {\rm e}^{{\rm j}2 \pi f \tau} \hspace{0.1cm} \rm d \it f.$$ | + | t \right] \cdot {\rm e}^{ {\rm j}2 \pi f \tau} \hspace{0.1cm} \rm d \it f.$$ |
Das innere Integral beschreibt das konjugiert–komplexe Spektrum $X_{\rm T}^{\star}(f)$. Daraus folgt weiter: | Das innere Integral beschreibt das konjugiert–komplexe Spektrum $X_{\rm T}^{\star}(f)$. Daraus folgt weiter: | ||
| − | :$${{\it \varphi}_x(\tau)} = \lim_{T_{\rm M}\to\infty}\hspace{0.2cm} | + | :$${ {\it \varphi}_x(\tau)} = \lim_{T_{\rm M}\to\infty}\hspace{0.2cm} |
| − | \frac{1}{ T_{\rm M}}\cdot \int^{+\infty}_{-\infty} | + | \frac{1}{ T_{\rm M} }\cdot \int^{+\infty}_{-\infty}\vert X_{\rm |
| − | T}(f) | + | T}(f)\vert^2 \cdot {\rm e}^{ {\rm j}2 \pi f \tau} \hspace{0.1cm} \rm d |
\it f.$$ | \it f.$$ | ||
Ein Vergleich mit dem bei Ergodizität stets gültigen Theorem von [https://de.wikipedia.org/wiki/Norbert_Wiener Wiener] und [https://de.wikipedia.org/wiki/Alexander_Jakowlewitsch_Chintschin Chintchine], | Ein Vergleich mit dem bei Ergodizität stets gültigen Theorem von [https://de.wikipedia.org/wiki/Norbert_Wiener Wiener] und [https://de.wikipedia.org/wiki/Alexander_Jakowlewitsch_Chintschin Chintchine], | ||
| − | :$${{\it \varphi}_x(\tau)} = \int^{+\infty}_{-\infty}{\it \Phi}_x(f) | + | :$${ {\it \varphi}_x(\tau)} = \int^{+\infty}_{-\infty}{\it \Phi}_x(f) |
| − | \cdot {\rm e}^{{\rm j}2 \pi f \tau} \hspace{0.1cm} \rm d \it f ,$$ | + | \cdot {\rm e}^{ {\rm j}2 \pi f \tau} \hspace{0.1cm} \rm d \it f ,$$ |
| − | zeigt die Gültigkeit der oben | + | zeigt die Gültigkeit der oben genannten Beziehung: |
| − | :$${{\it \Phi}_x(f)} = \lim_{T_{\rm M}\to\infty}\hspace{0.2cm} | + | :$${ {\it \Phi}_x(f)} = \lim_{T_{\rm M}\to\infty}\hspace{0.2cm} |
| − | \frac{1}{ T_{\rm M}}\cdot | + | \frac{1}{ T_{\rm M} }\cdot \vert X_{\rm T}(f)\vert^2.$$}} |
| − | |||
==Leistungsdichtespektrum des Filterausgangssignals== | ==Leistungsdichtespektrum des Filterausgangssignals== | ||
| + | <br> | ||
Kombiniert man die in den beiden letzten Abschnitten gemachten Aussagen, so kommt man zu folgendem wichtigen Ergebnis: | Kombiniert man die in den beiden letzten Abschnitten gemachten Aussagen, so kommt man zu folgendem wichtigen Ergebnis: | ||
| − | {{ | + | {{BlaueBox|TEXT= |
| − | + | $\text{Satz:}$ Das Leistungsdichtespektrum (LDS) am Ausgang eines linearen zeitinvarianten Systems mit dem Frequenzgang $H(f)$ ergibt sich als das Produkt aus dem Eingangs–LDS ${\it Φ}_x(f)$ und der Leistungsübertragungsfunktion $\vert H(f)\vert ^2$. | |
| − | :$${{\it \Phi}_y(f)} = {{\it \Phi}_x(f)} \cdot | + | :$${ {\it \Phi}_y(f)} = { {\it \Phi}_x(f)} \cdot \vert H(f)\vert ^2.$$}} |
| + | |||
| − | + | {{BlaueBox|TEXT= | |
| − | :$${{\it \Phi}_x(f)} =\hspace{-0.1cm} \lim_{T_{\rm M}\to\infty}\hspace{0.01cm} | + | $\text{Beweis:}$ Ausgegangen wird von den drei bereits vorher hergeleiteten Beziehungen: |
| − | \frac{1}{ T_{\rm M}}\hspace{-0.05cm}\cdot\hspace{-0.05cm} | + | :$${ {\it \Phi}_x(f)} =\hspace{-0.1cm} \lim_{T_{\rm M}\to\infty}\hspace{0.01cm} |
| − | {{\it \Phi}_y(f)} =\hspace{-0.1cm} \lim_{T_{\rm M}\to\infty}\hspace{0.01cm} | + | \frac{1}{ T_{\rm M} }\hspace{-0.05cm}\cdot\hspace{-0.05cm} \vert X_{\rm T}(f)\vert^2, \hspace{0.15cm} |
| − | \frac{1}{ T_{\rm M}}\hspace{-0.05cm}\cdot\hspace{-0.05cm} | + | { {\it \Phi}_y(f)} =\hspace{-0.1cm} \lim_{T_{\rm M}\to\infty}\hspace{0.01cm} |
| + | \frac{1}{ T_{\rm M} }\hspace{-0.05cm}\cdot\hspace{-0.05cm}\vert Y_{\rm T}(f)\vert^2, \hspace{0.15cm} | ||
Y_{\rm T}(f) = X_{\rm T}(f) \hspace{-0.05cm}\cdot\hspace{-0.05cm} H(f).$$ | Y_{\rm T}(f) = X_{\rm T}(f) \hspace{-0.05cm}\cdot\hspace{-0.05cm} H(f).$$ | ||
| − | Setzt man diese Gleichungen ineinander ein, so erhält man | + | Setzt man diese Gleichungen ineinander ein, so erhält man das obige Ergebnis. }} |
| − | + | ||
| + | |||
Das folgende Beispiel verdeutlicht den Zusammenhang bei Weißem Rauschen. | Das folgende Beispiel verdeutlicht den Zusammenhang bei Weißem Rauschen. | ||
| − | |||
[[File:P_ID468__Sto_T_5_1_S3_neu.png |right|frame| Filtereinfluss im Frequenzbereich]] | [[File:P_ID468__Sto_T_5_1_S3_neu.png |right|frame| Filtereinfluss im Frequenzbereich]] | ||
| − | + | {{GraueBox|TEXT= | |
| − | $$H(f) = {\rm e}^{- \pi \hspace{0.03cm}\cdot \hspace{0.03cm}(f/\Delta f)^2}$$ | + | $\text{Beispiel 1:}$ |
| − | liegt weißes Rauschen $x(t)$ mit der | + | Am Eingang eines Gauß-Tiefpasses mit Frequenzgang |
| − | $${{\it \Phi}_y(f)} = \frac {N_0}{2} \cdot {\rm e}^{- 2 \pi \hspace{0.03cm}\cdot \hspace{0.03cm}(f/\Delta | + | :$$H(f) = {\rm e}^{- \pi \hspace{0.03cm}\cdot \hspace{0.03cm}(f/\Delta f)^2}$$ |
| + | liegt weißes Rauschen $x(t)$ mit der Rauschleistungsdichte ${ {\it \Phi}_x(f)} =N_0/2$ (zweiseitige Darstellung)) an. | ||
| + | |||
| + | Dann gilt für das Leistungsdichtespektrum des Ausgangssignals: | ||
| + | :$${ {\it \Phi}_y(f)} = \frac {N_0}{2} \cdot {\rm e}^{- 2 \pi \hspace{0.03cm}\cdot \hspace{0.03cm}(f/\Delta | ||
f)^2}.$$ | f)^2}.$$ | ||
Die Grafik zeigt die Signale und Leistungsdichtespektren am Ein- und Ausgang des Filters. Anmerkungen: | Die Grafik zeigt die Signale und Leistungsdichtespektren am Ein- und Ausgang des Filters. Anmerkungen: | ||
*Das Eingangssignal $x(t)$ kann – streng genommen – gar nicht gezeichnet werden, da es eine unendlich große Leistung besitzt ⇒ Integral über ${\it Φ}_x(f)$ von $-\infty$ bis $+\infty$. | *Das Eingangssignal $x(t)$ kann – streng genommen – gar nicht gezeichnet werden, da es eine unendlich große Leistung besitzt ⇒ Integral über ${\it Φ}_x(f)$ von $-\infty$ bis $+\infty$. | ||
| − | *Das Ausgangssignal $y(t)$ ist niederfrequenter als $x(t)$ und besitzt eine endliche Leistung entsprechend dem Integral über ${\it Φ}_y(f)$. | + | *Das Ausgangssignal $y(t)$ ist niederfrequenter als $x(t)$ und besitzt eine endliche Leistung entsprechend dem Integral über ${\it Φ}_y(f)$.}} |
| − | |||
==Autokorrelationsfunktion des Filterausgangssignals== | ==Autokorrelationsfunktion des Filterausgangssignals== | ||
| + | <br> | ||
Das berechnete Leistungsdichtespektrum (LDS) kann auch wie folgt geschrieben werden: | Das berechnete Leistungsdichtespektrum (LDS) kann auch wie folgt geschrieben werden: | ||
:$${{\it \Phi}_y(f)} = {{\it \Phi}_x(f)} \cdot H(f) \cdot H^{\star}(f)$$ | :$${{\it \Phi}_y(f)} = {{\it \Phi}_x(f)} \cdot H(f) \cdot H^{\star}(f)$$ | ||
| − | {{ | + | |
| − | + | {{BlaueBox|TEXT= | |
| − | :$${{\it \varphi}_y(\tau)} = {{\it \varphi}_x(\tau)} \ast h(\tau)\ast h(- | + | $\text{Satz:}$ Für die zugehörige Autokorrelationsfunktion (AKF) erhält man dann entsprechend den Gesetzen der Fouriertransformation und durch Anwendung des [[Signaldarstellung/Faltungssatz_und_Faltungsoperation#Faltung_im_Zeitbereich|Faltungssatzes]]: |
| − | \tau).$$ | + | :$${ {\it \varphi}_y(\tau)} = { {\it \varphi}_x(\tau)} \ast h(\tau)\ast h(- |
| − | + | \tau).$$}} | |
| + | |||
| + | |||
Beim Übergang vom Spektral– in den Zeitbereich ist zu beachten: | Beim Übergang vom Spektral– in den Zeitbereich ist zu beachten: | ||
* Einzusetzen sind jeweils die Fourierrücktransformierten, nämlich | * Einzusetzen sind jeweils die Fourierrücktransformierten, nämlich | ||
| − | :$${{\it \varphi}_y(\tau)} \circ\hspace{0.05cm}\!\!\!-\!\!\!-\!\!\!-\!\!\bullet\,{{\it \Phi}_y(f)}, \hspace{0. | + | :$${{\it \varphi}_y(\tau)} \circ\hspace{0.05cm}\!\!\!-\!\!\!-\!\!\!-\!\!\bullet\,{{\it \Phi}_y(f)}, \hspace{0.5cm}{{\it \varphi}_x(\tau)} \circ\hspace{0.05cm}\!\!\!-\!\!\!-\!\!\!-\!\!\!\bullet\,{{\it \Phi}_x(f)}, \hspace{0.5cm}{h(\tau)} \circ\hspace{0.05cm}\!\!\!-\!\!\!-\!\!\!-\!\!\bullet\,{H(f)}, \hspace{0.5cm}{h(-\tau)} \circ\hspace{0.05cm}\!\!\!-\!\!\!-\!\!\!-\!\!\!\bullet\,{H^{\star}(f)}$$ |
*Zudem wird aus jeder Multiplikation eine Faltungsoperation. | *Zudem wird aus jeder Multiplikation eine Faltungsoperation. | ||
| − | |||
[[File:P_ID591__Sto_T_5_1_S4_neu.png |right|frame| Filtereinfluss im Zeitbereich]] | [[File:P_ID591__Sto_T_5_1_S4_neu.png |right|frame| Filtereinfluss im Zeitbereich]] | ||
| − | + | {{GraueBox|TEXT= | |
| − | Wir betrachten nochmals das | + | $\text{Beispiel 2:}$ |
| − | *weißes Rauschen ${{\it \Phi}_x(f)} =N_0/2$, | + | Wir betrachten nochmals das gleicheSzenario wie im Beispiel 1, aber diesmal im Zeitbereich: |
| + | *weißes Rauschen ${ {\it \Phi}_x(f)} =N_0/2$, | ||
*gaußförmiges Filter: | *gaußförmiges Filter: | ||
:$$H(f) = {\rm e}^{- \pi \hspace{0.03cm}\cdot \hspace{0.03cm}(f/\Delta f)^2}\hspace{0.1cm}\Rightarrow \hspace{0.1cm} | :$$H(f) = {\rm e}^{- \pi \hspace{0.03cm}\cdot \hspace{0.03cm}(f/\Delta f)^2}\hspace{0.1cm}\Rightarrow \hspace{0.1cm} | ||
| Line 136: | Line 159: | ||
*Durch zweimalige Faltung mit der (hier ebenfalls gaußförmigen) Impulsantwort $h(t)$ bzw. $h(–t)$ erhält man die AKF $φ_y(τ)$ des Ausgangssignals. Diese ist wiederum gaußförmig. | *Durch zweimalige Faltung mit der (hier ebenfalls gaußförmigen) Impulsantwort $h(t)$ bzw. $h(–t)$ erhält man die AKF $φ_y(τ)$ des Ausgangssignals. Diese ist wiederum gaußförmig. | ||
*Der AKF–Wert bei $τ = 0$ ist identisch mit der Fläche des Leistungsdichtespektrums ${\it Φ}_y(f)$ und kennzeichnet die Signalleistung (Varianz) $σ_y^2$. | *Der AKF–Wert bei $τ = 0$ ist identisch mit der Fläche des Leistungsdichtespektrums ${\it Φ}_y(f)$ und kennzeichnet die Signalleistung (Varianz) $σ_y^2$. | ||
| − | *Dagegen ergibt die Fläche unter $φ_y(τ)$ den LDS-Wert ${\it Φ}_y(f = \rm 0)$, also $N_0/2$. | + | *Dagegen ergibt die Fläche unter $φ_y(τ)$ den LDS-Wert ${\it Φ}_y(f = \rm 0)$, also $N_0/2$. }} |
| − | |||
| − | |||
| − | |||
==Kreuzkorrelationsfunktion zwischen Eingangs- und Ausgangssignal== | ==Kreuzkorrelationsfunktion zwischen Eingangs- und Ausgangssignal== | ||
| + | <br> | ||
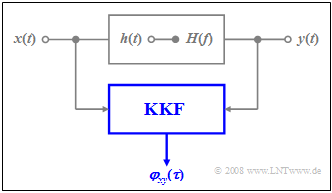
[[File:P_ID469__Sto_T_5_1_S5_Ganz_neu.png |frame| Zur KKF-Berechnung |right]] | [[File:P_ID469__Sto_T_5_1_S5_Ganz_neu.png |frame| Zur KKF-Berechnung |right]] | ||
Wir betrachten wieder ein Filter mit dem Frequenzgang $H(f)$ und der Impulsantwort $h(t)$. Weiter gilt: | Wir betrachten wieder ein Filter mit dem Frequenzgang $H(f)$ und der Impulsantwort $h(t)$. Weiter gilt: | ||
*Das stochastische Eingangssignal $x(t)$ ist eine Musterfunktion des ergodischen Zufallsprozesses $\{x(t)\}$. Die zugehörige Autokorrelationsfunktion (AKF) am Filtereingang ist somit $φ_x(τ)$, während das Leitsungsdichtespektrum (LDS) mit ${\it Φ}_x(f)$ bezeichnet wird. | *Das stochastische Eingangssignal $x(t)$ ist eine Musterfunktion des ergodischen Zufallsprozesses $\{x(t)\}$. Die zugehörige Autokorrelationsfunktion (AKF) am Filtereingang ist somit $φ_x(τ)$, während das Leitsungsdichtespektrum (LDS) mit ${\it Φ}_x(f)$ bezeichnet wird. | ||
| − | *Die entsprechenden Beschreibungsgrößen des ergodischen Zufallsprozesses $\{y(t)\}$ am Filterausgang sind die Musterfunktion $ | + | *Die entsprechenden Beschreibungsgrößen des ergodischen Zufallsprozesses $\{y(t)\}$ am Filterausgang sind die Musterfunktion $y(t)$, die Autokorrelationsfunktion $φ_y(τ)$ sowie das Leitsungsdichtespektrum ${\it Φ}_y(f)$. |
| − | + | <br clear=all> | |
| − | + | {{BlaueBox|TEXT= | |
| − | {{ | + | $\text{Satz:}$ Für die '''Kreuzkorrelationsfunktion''' (KKF) zwischen dem Eingangs– und dem Ausgangssignal gilt: |
| − | + | :$${ {\it \varphi}_{xy}(\tau)} = h(\tau)\ast { {\it \varphi}_x(\tau)} .$$ | |
| − | :$${{\it \varphi}_{xy}(\tau)} = h(\tau)\ast {{\it \varphi}_x(\tau)} .$$ | + | Hierbei bezeichnet $h(τ)$ ist die Impulsantwort des Filters (mit der Zeitvariablen $τ$ anstelle von $t$).}} |
| − | Hierbei bezeichnet $h(τ)$ ist die Impulsantwort des Filters (mit der Zeitvariablen $τ$ anstelle von $t$). | ||
| − | {{ | + | {{BlaueBox|TEXT= |
| − | + | $\text{Beweis:}$ Allgemein gilt für die Kreuzkorrelationsfunktion zwischen zwei Signalen $x(t)$ und $y(t)$: | |
| − | :$${{\it \varphi}_{xy}(\tau)} = \lim_{T_{\rm M}\to\infty}\hspace{0.2cm}\frac{1}{ T_{\rm M}}\cdot\int^{+T_{\rm M}/2}_{-T_{\rm M}/2}x(t)\cdot y(t + \tau)\hspace{0.1cm} \rm d \it t.$$ | + | :$${ {\it \varphi}_{xy}(\tau)} = \lim_{T_{\rm M}\to\infty}\hspace{0.2cm}\frac{1}{ T_{\rm M} }\cdot\int^{+T_{\rm M}/2}_{-T_{\rm M}/2}x(t)\cdot y(t + \tau)\hspace{0.1cm} \rm d \it t.$$ |
| − | Mit der allgemeingültigen Beziehung $y(t) = h(t) \ast x(t)$ und der formalen Integrationsvariablen $θ$ lässt sich hierfür auch schreiben: | + | Mit der allgemeingültigen Beziehung $y(t) = h(t) \ast x(t)$ und der formalen Integrationsvariablen $θ$ lässt sich hierfür auch schreiben: |
| − | :$${{\it \varphi}_{xy}(\tau)} = \lim_{T_{\rm M}\to\infty}\hspace{0.2cm}\frac{1}{ T_{\rm M}}\cdot\int^{+T_{\rm M}/2}_{-T_{\rm M}/2}x(t)\cdot \int^{+\infty}_{-\infty} h(\theta) \cdot x(t + \tau - \theta)\hspace{0.1cm}{\rm d}\theta\hspace{0.1cm}{\rm d} \it t.$$ | + | :$${ {\it \varphi}_{xy}(\tau)} = \lim_{T_{\rm M}\to\infty}\hspace{0.2cm}\frac{1}{ T_{\rm M} }\cdot\int^{+T_{\rm M}/2}_{-T_{\rm M}/2}x(t)\cdot \int^{+\infty}_{-\infty} h(\theta) \cdot x(t + \tau - \theta)\hspace{0.1cm}{\rm d}\theta\hspace{0.1cm}{\rm d} \it t.$$ |
Durch Vertauschen der beiden Integrale und Hereinziehen der Grenzwertbildung erhält man: | Durch Vertauschen der beiden Integrale und Hereinziehen der Grenzwertbildung erhält man: | ||
| − | :$${{\it \varphi}_{xy}(\tau)} = \int^{+\infty}_{-\infty} | + | :$${ {\it \varphi}_{xy}(\tau)} = \int^{+\infty}_{-\infty} |
h(\theta) \cdot \left[ \lim_{T_{\rm M}\to\infty}\hspace{0.2cm} | h(\theta) \cdot \left[ \lim_{T_{\rm M}\to\infty}\hspace{0.2cm} | ||
| − | \frac{1}{ T_{\rm M}} \cdot\int^{+T_{\rm M}/2}_{-T_{\rm | + | \frac{1}{ T_{\rm M} } \cdot\int^{+T_{\rm M}/2}_{-T_{\rm |
M}/2}x(t)\cdot x(t + \tau - \theta)\hspace{0.1cm} | M}/2}x(t)\cdot x(t + \tau - \theta)\hspace{0.1cm} | ||
\hspace{0.1cm} {\rm d} t \right]{\rm d}\theta.$$ | \hspace{0.1cm} {\rm d} t \right]{\rm d}\theta.$$ | ||
| − | Der Ausdruck in den eckigen Klammern ergibt den AKF-Wert am Eingang zum Zeitpunkt $τ | + | Der Ausdruck in den eckigen Klammern ergibt den AKF-Wert am Eingang zum Zeitpunkt $τ - θ$: |
| − | :$${{\it \varphi}_{xy}(\tau)} = \int^{+\infty}_{-\infty}h(\theta) \cdot \varphi_x(\tau - \theta)\hspace{0.1cm}\hspace{0.1cm} {\rm d}\theta = h(\tau)\ast {{\it \varphi}_x(\tau)} .$$ | + | :$${ {\it \varphi}_{xy}(\tau)} = \int^{+\infty}_{-\infty}h(\theta) \cdot \varphi_x(\tau - \theta)\hspace{0.1cm}\hspace{0.1cm} {\rm d}\theta = h(\tau)\ast { {\it \varphi}_x(\tau)} .$$ |
| − | Das verbleibende Integral beschreibt aber die Faltungsoperation in ausführlicher Schreibweise. | + | Das verbleibende Integral beschreibt aber die Faltungsoperation in ausführlicher Schreibweise. }} |
| − | Im Frequenzbereich lautet die entsprechende Gleichung: | + | {{BlaueBox|TEXT= |
| − | $${{\it \Phi}_{xy}(f)} = H(f)\cdot{{\it \Phi}_x(f)} .$$ | + | $\text{Fazit:}$ Im Frequenzbereich lautet die entsprechende Gleichung: |
| + | :$${ {\it \Phi}_{xy}(f)} = H(f)\cdot{ {\it \Phi}_x(f)} .$$ | ||
Die beiden Gleichungen zeigen, dass der Filterfrequenzgang $H(f)$ aus einer Messung mit stochastischer Anregung vollständig – also sowohl der Betrag als auch die Phase – berechnet werden kann, wenn folgende Beschreibungsgrößen ermittelt werden: | Die beiden Gleichungen zeigen, dass der Filterfrequenzgang $H(f)$ aus einer Messung mit stochastischer Anregung vollständig – also sowohl der Betrag als auch die Phase – berechnet werden kann, wenn folgende Beschreibungsgrößen ermittelt werden: | ||
*die statistischen Kenngrößen am Eingang, entweder die AKF $φ_x(τ)$ oder das LDS ${\it Φ}_x(f)$, | *die statistischen Kenngrößen am Eingang, entweder die AKF $φ_x(τ)$ oder das LDS ${\it Φ}_x(f)$, | ||
| − | *sowie die Kreuzkorrelationsfunktion $φ_{xy}(τ)$ bzw. deren Fouriertransformierte ${\it Φ}_{xy}(f)$. | + | *sowie die Kreuzkorrelationsfunktion $φ_{xy}(τ)$ bzw. deren Fouriertransformierte ${\it Φ}_{xy}(f)$. }} |
==Aufgaben zum Kapitel== | ==Aufgaben zum Kapitel== | ||
| + | <br> | ||
| + | [[Aufgaben:5.1 Gaußsche AKF und Gaußtiefpass|Aufgabe 5.1: Gaußsche AKF und Gaußtiefpass]] | ||
| − | + | [[Aufgaben:5.1Z cos^2-Rauschbegrenzung|Aufgabe 5.1Z: $\cos^2$-Rauschbegrenzung]] | |
| − | |||
| − | [[Aufgaben:5.1Z cos^2-Rauschbegrenzung|Aufgabe 5.1Z: | ||
| − | [[Aufgaben:5.2 Frequenzgangbestimmung|Aufgabe 5.2: | + | [[Aufgaben:5.2 Frequenzgangbestimmung|Aufgabe 5.2: Bestimmung des Frequenzgangs]] |
| − | [[Aufgaben:5.2Z Zweiwegekanal|Aufgabe 5.2Z: | + | [[Aufgaben:5.2Z Zweiwegekanal|Aufgabe 5.2Z: Zweiwegekanal]] |
{{Display}} | {{Display}} | ||
Revision as of 13:40, 13 April 2018
Contents
# ÜBERBLICK ZUM FÜNFTEN HAUPTKAPITEL #
Dieses Kapitel beschreibt den Einfluss eines Filters auf die Autokorrelationsfunktion (AKF) und das Leistungsdichtespektrum (LDS) stochastischer Signalen. Im Einzelnen werden behandelt:
- die Berechnung von AKF und LDS am Filterausgang (Stochastische Systemtheorie),
- die Struktur und die Darstellung Digitaler Filter (nichrekursiv und rekursiv),
- die Dimensionierung der Filterkoeffizienten für eine vorgegebene AKF,
- die Bedeutung des Matched-Filters für Nachrichtensysteme (SNR-Maximierung),
- die Eigenschaften des Wiener-Kolmogorow-Filters zur Signalrekonstruktion.
Weitere Informationen zum Thema „Filterung stochastischer Signale” sowie Aufgaben, Simulationen und Programmierübungen finden Sie im
- Kapitel 10: Filterung stochastischer Signale (Programm fil)
- Kapitel 11: Optimale Filter (Programm ofi)
des Praktikums „Simulationsmethoden in der Nachrichtentechnik”. Diese (ehemalige) LNT-Lehrveranstaltung an der TU München basiert auf
- dem Lehrsoftwarepaket LNTsim ⇒ Link verweist auf die ZIP-Version des Programms, und
- der Praktikumsanleitung - Teil B ⇒ Link verweist auf die PDF-Version mit Kapitel 10: Seite 229-248 und Kapitel 11: Seite 249-270.
Problemstellung
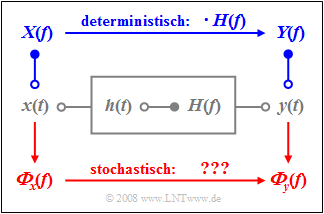
Wir betrachten wie im Buch Lineare zeitinvariante Systeme die rechts skizzierte Anordnung, wobei das System
- sowohl durch die Impulsantwort $h(t)$
- als auch durch seinen Frequenzgang $H(f)$
eindeutig beschrieben ist. Der Zusammenhang zwischen diesen Beschreibungsgrößen im Zeit– und Frequenzbereich ist durch die Fouriertransformation gegeben.
Legt man an den Eingang das Signal $x(t)$ an und bezeichnet das Ausgangssignal mit $y(t)$, so liefert die klassische Systemtheorie folgende Aussagen:
- Das Ausgangssignal $y(t)$ ergibt sich aus der Faltung zwischen dem Eingangssignal $x(t)$ und der Impulsantwort $h(t)$:
- $$y(t) = x(t) \ast h(t) = \int_{-\infty}^{+\infty} x(\tau)\cdot h ( t - \tau) \,\,{\rm d}\tau.$$
- Diese Gleichung gilt für deterministische und stochastische Signale gleichermaßen.
- Bei deterministischen Signalen geht man meist den Umweg über die Spektralfunktionen. Das Spektrum $X(f)$ ist die Fouriertransformierte von $x(t)$. Die Multiplikation mit dem Frequenzgang $H(f)$ führt zum Ausgangsspektrum $Y(f)$. Darauslässt sich das Signal $y(t)$ durch die Fourierrücktransformation gewinnen.
- Bei stochastischen Signalen versagt diese Vorgehensweise, da dann die Zeitfunktionen $x(t)$ und $y(t)$ nicht für alle Zeiten von $–∞$ bis $+∞$ vorhersagbar sind und somit die dazugehörigen Amplitudenspektren $X(f)$ und $Y(f)$ gar nicht existieren. In diesem Fall muss auf die im letzten Kapitel definierten Leistungsdichtespektren übergegangen werden.
Amplituden- und Leistungsdichtespektrum
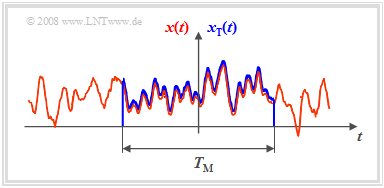
Wir betrachten einen ergodischen Zufallsprozess $\{x(t)\}$, dessen Autokorrelationsfunktion $φ_x(τ)$ als bekannt vorausgesetzt wird. Das Leistungsdichtespektrum ${\it Φ}_x(f)$ ist dann über die Fouriertransformation ebenfalls eindeutig bestimmt und es gelten die folgenden Aussagen:
- Das Leistungsdichtespektrum ${\it Φ}_x(f)$ kann – ebenso wie die Autokorrelationsfunktion $φ_x(τ)$ – für jede einzelne Musterfunktion des stationären und ergodischen Zufallsprozesses $\{x(t)\}$ angegeben werden, auch wenn der spezifische Verlauf von $x(t)$ explizit nicht bekannt ist.
- Das Amplitudenspektrum $X(f)$ ist dagegen undefiniert, da bei Kenntnis der Spektralfunktion $X(f)$ auch die gesamte Zeitfunktion $x(t)$ von $–∞$ bis $+∞$ über die Fourierrücktransformation bekannt sein müsste, was bei einem stochastischen Signal eindeutig nicht der Fall sein kann.
- Ist entsprechend der nebenstehenden Skizze ein Zeitausschnitt der endlichen Zeitdauer $T_{\rm M}$ bekannt, so kann für diesen natürlich wieder die Fouriertransformation angewandt werden.
$\text{Satz:}$ Zwischen dem Leistungsdichtespektrum ${\it Φ}_x(f)$ des unendlich ausgedehnten Zufallssignals $x(t)$ und dem Amplitudenspektrum $X_{\rm T}(f)$ des begrenzten Zeitausschnittes $x_{\rm T}(t)$ besteht der folgende Zusammenhang:
- $${ {\it \Phi}_x(f)} = \lim_{T_{\rm M}\to\infty}\hspace{0.2cm} \frac{1}{ T_{\rm M} }\cdot \vert X_{\rm T}(f)\vert ^2.$$
$\text{Beweis:}$ Vorne wurde die Autokorrelationsfunktion eines ergodischen Prozesses mit der Musterfunktion $x(t)$ wie folgt angegeben:
- $${ {\it \varphi}_x(\tau)} = \lim_{T_{\rm M}\to\infty}\hspace{0.2cm} \frac{1}{ T_{\rm M} }\cdot\int^{+T_{\rm M}/2}_{-T_{\rm M}/2}x(t)\cdot x(t + \tau)\hspace{0.1cm} \rm d \it t.$$
Es ist zulässig, die zeitlich unbegrenzte Funktion $x(t)$ durch die auf den Zeitbereich $-T_{\rm M}/2$ bis $+T_{\rm M}/2$ begrenzte Funktion $x_{\rm T}(t)$ zu ersetzen. $x_{\rm T}(t)$ korrespondiert mit dem Spektrum $X_{\rm T}(f)$, und man erhält durch Anwendung des ersten Fourierintegrals und des Verschiebungssatzes:
- $${ {\it \varphi}_x(\tau)} = \lim_{T_{\rm M}\to\infty}\hspace{0.2cm} \frac{1}{ T_{\rm M} }\cdot \int^{+T_{\rm M}/2}_{-T_{\rm M}/2}x_{\rm T}(t)\cdot \int^{+\infty}_{-\infty}X_{\rm T}(f)\cdot {\rm e}^{ {\rm j}2 \pi f ( t + \tau) } \hspace{0.1cm} \rm d \it f \hspace{0.1cm} \rm d \it t.$$
Nach Aufspalten des Exponenten und Vertauschen von Zeit- und Frequenzintegral ergibt sich:
- $${ {\it \varphi}_x(\tau)} = \lim_{T_{\rm M}\to\infty}\hspace{0.2cm} \frac{1}{ T_{\rm M} }\cdot \int^{+\infty}_{-\infty}X_{\rm T}(f)\cdot \left[ \int^{+T_{\rm M}/2}_{-T_{\rm M}/2}x_{\rm T}(t)\cdot {\rm e}^{ {\rm j}2 \pi f t } \hspace{0.1cm} \rm d \it t \right] \cdot {\rm e}^{ {\rm j}2 \pi f \tau} \hspace{0.1cm} \rm d \it f.$$
Das innere Integral beschreibt das konjugiert–komplexe Spektrum $X_{\rm T}^{\star}(f)$. Daraus folgt weiter:
- $${ {\it \varphi}_x(\tau)} = \lim_{T_{\rm M}\to\infty}\hspace{0.2cm} \frac{1}{ T_{\rm M} }\cdot \int^{+\infty}_{-\infty}\vert X_{\rm T}(f)\vert^2 \cdot {\rm e}^{ {\rm j}2 \pi f \tau} \hspace{0.1cm} \rm d \it f.$$
Ein Vergleich mit dem bei Ergodizität stets gültigen Theorem von Wiener und Chintchine,
- $${ {\it \varphi}_x(\tau)} = \int^{+\infty}_{-\infty}{\it \Phi}_x(f) \cdot {\rm e}^{ {\rm j}2 \pi f \tau} \hspace{0.1cm} \rm d \it f ,$$
zeigt die Gültigkeit der oben genannten Beziehung:
- $${ {\it \Phi}_x(f)} = \lim_{T_{\rm M}\to\infty}\hspace{0.2cm} \frac{1}{ T_{\rm M} }\cdot \vert X_{\rm T}(f)\vert^2.$$
Leistungsdichtespektrum des Filterausgangssignals
Kombiniert man die in den beiden letzten Abschnitten gemachten Aussagen, so kommt man zu folgendem wichtigen Ergebnis:
$\text{Satz:}$ Das Leistungsdichtespektrum (LDS) am Ausgang eines linearen zeitinvarianten Systems mit dem Frequenzgang $H(f)$ ergibt sich als das Produkt aus dem Eingangs–LDS ${\it Φ}_x(f)$ und der Leistungsübertragungsfunktion $\vert H(f)\vert ^2$.
- $${ {\it \Phi}_y(f)} = { {\it \Phi}_x(f)} \cdot \vert H(f)\vert ^2.$$
$\text{Beweis:}$ Ausgegangen wird von den drei bereits vorher hergeleiteten Beziehungen:
- $${ {\it \Phi}_x(f)} =\hspace{-0.1cm} \lim_{T_{\rm M}\to\infty}\hspace{0.01cm} \frac{1}{ T_{\rm M} }\hspace{-0.05cm}\cdot\hspace{-0.05cm} \vert X_{\rm T}(f)\vert^2, \hspace{0.15cm} { {\it \Phi}_y(f)} =\hspace{-0.1cm} \lim_{T_{\rm M}\to\infty}\hspace{0.01cm} \frac{1}{ T_{\rm M} }\hspace{-0.05cm}\cdot\hspace{-0.05cm}\vert Y_{\rm T}(f)\vert^2, \hspace{0.15cm} Y_{\rm T}(f) = X_{\rm T}(f) \hspace{-0.05cm}\cdot\hspace{-0.05cm} H(f).$$
Setzt man diese Gleichungen ineinander ein, so erhält man das obige Ergebnis.
Das folgende Beispiel verdeutlicht den Zusammenhang bei Weißem Rauschen.
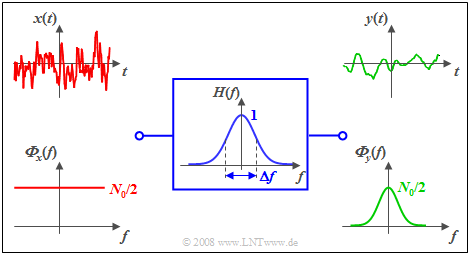
$\text{Beispiel 1:}$ Am Eingang eines Gauß-Tiefpasses mit Frequenzgang
- $$H(f) = {\rm e}^{- \pi \hspace{0.03cm}\cdot \hspace{0.03cm}(f/\Delta f)^2}$$
liegt weißes Rauschen $x(t)$ mit der Rauschleistungsdichte ${ {\it \Phi}_x(f)} =N_0/2$ (zweiseitige Darstellung)) an.
Dann gilt für das Leistungsdichtespektrum des Ausgangssignals:
- $${ {\it \Phi}_y(f)} = \frac {N_0}{2} \cdot {\rm e}^{- 2 \pi \hspace{0.03cm}\cdot \hspace{0.03cm}(f/\Delta f)^2}.$$
Die Grafik zeigt die Signale und Leistungsdichtespektren am Ein- und Ausgang des Filters. Anmerkungen:
- Das Eingangssignal $x(t)$ kann – streng genommen – gar nicht gezeichnet werden, da es eine unendlich große Leistung besitzt ⇒ Integral über ${\it Φ}_x(f)$ von $-\infty$ bis $+\infty$.
- Das Ausgangssignal $y(t)$ ist niederfrequenter als $x(t)$ und besitzt eine endliche Leistung entsprechend dem Integral über ${\it Φ}_y(f)$.
Autokorrelationsfunktion des Filterausgangssignals
Das berechnete Leistungsdichtespektrum (LDS) kann auch wie folgt geschrieben werden:
- $${{\it \Phi}_y(f)} = {{\it \Phi}_x(f)} \cdot H(f) \cdot H^{\star}(f)$$
$\text{Satz:}$ Für die zugehörige Autokorrelationsfunktion (AKF) erhält man dann entsprechend den Gesetzen der Fouriertransformation und durch Anwendung des Faltungssatzes:
- $${ {\it \varphi}_y(\tau)} = { {\it \varphi}_x(\tau)} \ast h(\tau)\ast h(- \tau).$$
Beim Übergang vom Spektral– in den Zeitbereich ist zu beachten:
- Einzusetzen sind jeweils die Fourierrücktransformierten, nämlich
- $${{\it \varphi}_y(\tau)} \circ\hspace{0.05cm}\!\!\!-\!\!\!-\!\!\!-\!\!\bullet\,{{\it \Phi}_y(f)}, \hspace{0.5cm}{{\it \varphi}_x(\tau)} \circ\hspace{0.05cm}\!\!\!-\!\!\!-\!\!\!-\!\!\!\bullet\,{{\it \Phi}_x(f)}, \hspace{0.5cm}{h(\tau)} \circ\hspace{0.05cm}\!\!\!-\!\!\!-\!\!\!-\!\!\bullet\,{H(f)}, \hspace{0.5cm}{h(-\tau)} \circ\hspace{0.05cm}\!\!\!-\!\!\!-\!\!\!-\!\!\!\bullet\,{H^{\star}(f)}$$
- Zudem wird aus jeder Multiplikation eine Faltungsoperation.
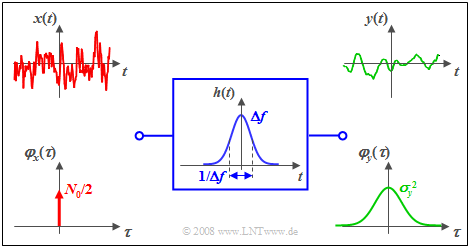
$\text{Beispiel 2:}$ Wir betrachten nochmals das gleicheSzenario wie im Beispiel 1, aber diesmal im Zeitbereich:
- weißes Rauschen ${ {\it \Phi}_x(f)} =N_0/2$,
- gaußförmiges Filter:
- $$H(f) = {\rm e}^{- \pi \hspace{0.03cm}\cdot \hspace{0.03cm}(f/\Delta f)^2}\hspace{0.1cm}\Rightarrow \hspace{0.1cm} h(t) = \Delta f \cdot {\rm e}^{- \pi \hspace{0.03cm}\cdot \hspace{0.03cm}(\Delta f \hspace{0.03cm}\cdot \hspace{0.03cm}t)^2}.$$
Man erkennt aus dieser Darstellung:
- Die AKF des Eingangssignals ist nun eine Diracfunktion mit dem Gewicht $N_0/2$.
- Durch zweimalige Faltung mit der (hier ebenfalls gaußförmigen) Impulsantwort $h(t)$ bzw. $h(–t)$ erhält man die AKF $φ_y(τ)$ des Ausgangssignals. Diese ist wiederum gaußförmig.
- Der AKF–Wert bei $τ = 0$ ist identisch mit der Fläche des Leistungsdichtespektrums ${\it Φ}_y(f)$ und kennzeichnet die Signalleistung (Varianz) $σ_y^2$.
- Dagegen ergibt die Fläche unter $φ_y(τ)$ den LDS-Wert ${\it Φ}_y(f = \rm 0)$, also $N_0/2$.
Kreuzkorrelationsfunktion zwischen Eingangs- und Ausgangssignal
Wir betrachten wieder ein Filter mit dem Frequenzgang $H(f)$ und der Impulsantwort $h(t)$. Weiter gilt:
- Das stochastische Eingangssignal $x(t)$ ist eine Musterfunktion des ergodischen Zufallsprozesses $\{x(t)\}$. Die zugehörige Autokorrelationsfunktion (AKF) am Filtereingang ist somit $φ_x(τ)$, während das Leitsungsdichtespektrum (LDS) mit ${\it Φ}_x(f)$ bezeichnet wird.
- Die entsprechenden Beschreibungsgrößen des ergodischen Zufallsprozesses $\{y(t)\}$ am Filterausgang sind die Musterfunktion $y(t)$, die Autokorrelationsfunktion $φ_y(τ)$ sowie das Leitsungsdichtespektrum ${\it Φ}_y(f)$.
$\text{Satz:}$ Für die Kreuzkorrelationsfunktion (KKF) zwischen dem Eingangs– und dem Ausgangssignal gilt:
- $${ {\it \varphi}_{xy}(\tau)} = h(\tau)\ast { {\it \varphi}_x(\tau)} .$$
Hierbei bezeichnet $h(τ)$ ist die Impulsantwort des Filters (mit der Zeitvariablen $τ$ anstelle von $t$).
$\text{Beweis:}$ Allgemein gilt für die Kreuzkorrelationsfunktion zwischen zwei Signalen $x(t)$ und $y(t)$:
- $${ {\it \varphi}_{xy}(\tau)} = \lim_{T_{\rm M}\to\infty}\hspace{0.2cm}\frac{1}{ T_{\rm M} }\cdot\int^{+T_{\rm M}/2}_{-T_{\rm M}/2}x(t)\cdot y(t + \tau)\hspace{0.1cm} \rm d \it t.$$
Mit der allgemeingültigen Beziehung $y(t) = h(t) \ast x(t)$ und der formalen Integrationsvariablen $θ$ lässt sich hierfür auch schreiben:
- $${ {\it \varphi}_{xy}(\tau)} = \lim_{T_{\rm M}\to\infty}\hspace{0.2cm}\frac{1}{ T_{\rm M} }\cdot\int^{+T_{\rm M}/2}_{-T_{\rm M}/2}x(t)\cdot \int^{+\infty}_{-\infty} h(\theta) \cdot x(t + \tau - \theta)\hspace{0.1cm}{\rm d}\theta\hspace{0.1cm}{\rm d} \it t.$$
Durch Vertauschen der beiden Integrale und Hereinziehen der Grenzwertbildung erhält man:
- $${ {\it \varphi}_{xy}(\tau)} = \int^{+\infty}_{-\infty} h(\theta) \cdot \left[ \lim_{T_{\rm M}\to\infty}\hspace{0.2cm} \frac{1}{ T_{\rm M} } \cdot\int^{+T_{\rm M}/2}_{-T_{\rm M}/2}x(t)\cdot x(t + \tau - \theta)\hspace{0.1cm} \hspace{0.1cm} {\rm d} t \right]{\rm d}\theta.$$
Der Ausdruck in den eckigen Klammern ergibt den AKF-Wert am Eingang zum Zeitpunkt $τ - θ$:
- $${ {\it \varphi}_{xy}(\tau)} = \int^{+\infty}_{-\infty}h(\theta) \cdot \varphi_x(\tau - \theta)\hspace{0.1cm}\hspace{0.1cm} {\rm d}\theta = h(\tau)\ast { {\it \varphi}_x(\tau)} .$$
Das verbleibende Integral beschreibt aber die Faltungsoperation in ausführlicher Schreibweise.
$\text{Fazit:}$ Im Frequenzbereich lautet die entsprechende Gleichung:
- $${ {\it \Phi}_{xy}(f)} = H(f)\cdot{ {\it \Phi}_x(f)} .$$
Die beiden Gleichungen zeigen, dass der Filterfrequenzgang $H(f)$ aus einer Messung mit stochastischer Anregung vollständig – also sowohl der Betrag als auch die Phase – berechnet werden kann, wenn folgende Beschreibungsgrößen ermittelt werden:
- die statistischen Kenngrößen am Eingang, entweder die AKF $φ_x(τ)$ oder das LDS ${\it Φ}_x(f)$,
- sowie die Kreuzkorrelationsfunktion $φ_{xy}(τ)$ bzw. deren Fouriertransformierte ${\it Φ}_{xy}(f)$.
Aufgaben zum Kapitel
Aufgabe 5.1: Gaußsche AKF und Gaußtiefpass
Aufgabe 5.1Z: $\cos^2$-Rauschbegrenzung
Aufgabe 5.2: Bestimmung des Frequenzgangs