Aufgaben:Exercise 5.7: McCullough and Gilbert-Elliott Parameters

• Return to book

Gilbert-Elliott– und McCullough–Modell

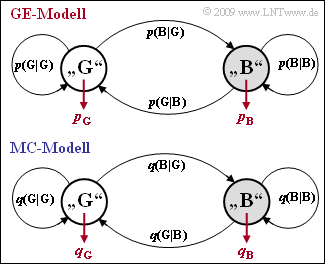
In Aufgabe 5.6 und Aufgabe 5.6Z wurden jeweils das GE–Modell mit den Parameterwerten

$$p_{\rm G} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 0.001, \hspace{0.2cm}p_{\rm B} = 0.1,\hspace{0.2cm} {\rm Pr}(\rm G\hspace{0.05cm}|\hspace{0.05cm} B)\hspace{-0.1cm} \ = \ \hspace{-0.1cm} 0.1, \hspace{0.2cm} {\rm Pr}(\rm B\hspace{0.05cm}|\hspace{0.05cm} G) = 0.01\hspace{0.05cm}.$$

genauer untersucht. Gegenüber diesen Aufgaben werden nun die Übergangswahrscheinlichkeiten umbenannt, beispielsweise wird $p(\rm B\hspace{0.05cm}|\hspace{0.05cm}G)$ anstelle von $\rm Pr(B\hspace{0.05cm}|\hspace{0.05cm}G)$ geschrieben. In der oberen Grafik ist diese Umbenennung bereits vorgenommen.

Die untere Grafik zeigt das MC–Modell von McCullough. Dieses besitzt die genau gleiche Struktur wie das GE–Modell, doch werden nun alle Wahrscheinlichkeiten mit $q$ anstelle von $p$ bezeichnet.

Beispielsweise bezeichnet beim MC–Modell $q\rm (B\hspace{0.05cm}|\hspace{0.05cm}G)$ die Übergangswahrscheinlichkeit von Zustand $\rm G$ in den Zustand$\rm B$ unter der Voraussetzung, dass im Zustand $\rm G$ gerade ein Fehler aufgetreten ist. Der GE–Parameter $p \rm (B\hspace{0.05cm}|\hspace{0.05cm}G)$ kennzeichnet dagegen diese Übergangswahrscheinlichkeit ohne Zusatzbedingung.

Die Parameter des GE–Modells   ⇒   $p_{\rm G}, p_{\rm B}, p({\rm B\hspace{0.05cm}|\hspace{0.05cm}G}), p({\rm G\hspace{0.05cm}|\hspace{0.05cm}B})$ können so in die entsprechenden MC–Parameter $q_{\rm G}, q_{\rm B}, q({\rm B\hspace{0.05cm}|\hspace{0.05cm}G})$ und $q({\rm G\hspace{0.05cm}|\hspace{0.05cm}B})$ umgerechnet werden, dass eine in ihren statistischen Eigenschaften gleiche Fehlerfolge wie beim GE–Modell erzeugt wird, allerdings nicht die identische Folge.

Die Umrechnungsgleichungen lauten:

$$q_{\rm G} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 1-\beta_{\rm G}\hspace{0.05cm}, \hspace{0.2cm}q_{\rm B} = 1-\beta_{\rm B}\hspace{0.05cm},\hspace{0.5cm} q(\rm B\hspace{0.05cm}|\hspace{0.05cm} G ) \hspace{-0.1cm} \ = \ \hspace{-0.1cm}\frac{\alpha_{\rm B} \cdot[{\rm Pr}(\rm B\hspace{0.05cm}|\hspace{0.05cm} G ) + {\rm Pr}(\rm G\hspace{0.05cm}|\hspace{0.05cm} B )]}{\alpha_{\rm G} \cdot q_{\rm B} + \alpha_{\rm B} \cdot q_{\rm G}} \hspace{0.05cm},\hspace{0.5cm} \hspace{0.2cm}q(\rm G\hspace{0.05cm}|\hspace{0.05cm} B )\hspace{-0.1cm} \ = \ \hspace{-0.1cm} \frac{\alpha_{\rm G}}{\alpha_{\rm B}} \cdot q(\rm B\hspace{0.05cm}|\hspace{0.05cm} G )\hspace{0.05cm}.$$

Hierbei sind die folgenden Hilfsgrößen verwendet:

$$u_{\rm GG} \hspace{-0.1cm} \ = \ \hspace{-0.1cm}{\rm Pr}(\rm G\hspace{0.05cm}|\hspace{0.05cm} G ) \cdot (1-{\it p}_{\rm G}) \hspace{0.05cm},\hspace{0.2cm} {\it u}_{\rm GB} ={\rm Pr}(\rm B\hspace{0.05cm}|\hspace{0.05cm} G ) \cdot (1-{\it p}_{\hspace{0.03cm} \rm G}) \hspace{0.05cm},$$

$$u_{\rm BB} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {\rm Pr}(\rm B\hspace{0.05cm}|\hspace{0.05cm} B ) \cdot (1-{\it p}_{\hspace{0.03cm}\rm B}) \hspace{0.05cm},\hspace{0.29cm} {\it u}_{\rm BG} ={\rm Pr}(\rm G\hspace{0.05cm}|\hspace{0.05cm} B ) \cdot (1-{\it p}_{\hspace{0.03cm}\rm B})\hspace{0.05cm}$$

$$\Rightarrow \hspace{0.3cm} \beta_{\rm G} \hspace{-0.1cm} \ = \ \hspace{-0.1cm}\frac{u_{\rm GG} + u_{\rm BB} + \sqrt{(u_{\rm GG} - u_{\rm BB})^2 + 4 \cdot u_{\rm GB}\cdot u_{\rm BG}}}{2} \hspace{0.05cm},$$

$$\beta_{\rm B} \hspace{-0.1cm} \ = \ \hspace{-0.1cm}\frac{u_{\rm GG} + u_{\rm BB} - \sqrt{(u_{\rm GG} - u_{\rm BB})^2 + 4 \cdot u_{\rm GB}\cdot u_{\rm BG}}}{2}\hspace{0.05cm},$$

$$x_{\rm G} =\frac{u_{\rm BG}}{\beta_{\rm G}-u_{\rm BB}} \hspace{0.05cm},\hspace{0.2cm} x_{\rm B} =\frac{u_{\rm BG}}{\beta_{\rm B}-u_{\rm BB}}$$

$$\Rightarrow \hspace{0.3cm} \alpha_{\rm G} = \frac{(w_{\rm G} \cdot p_{\rm G} + w_{\rm B} \cdot p_{\rm B}\cdot x_{\rm G})( x_{\rm B}-1)}{p_{\rm M} \cdot( x_{\rm B}-x_{\rm G})} \hspace{0.05cm}, \hspace{0.2cm}\alpha_{\rm B} = 1-\alpha_{\rm G}\hspace{0.05cm}.$$

$w_{\rm G}$ und $w_{\rm B}$ sind die Zustandswahrscheinlichkeiten für „GOOD” und „BAD” des GE–Modells. In der Aufgabe 5.6Z wurden diese wie folgt berechnet:

$$w_{\rm G} = {10}/{11}\hspace{0.05cm}, \hspace{0.2cm}w_{\rm B} = {1}/{11}\hspace{0.05cm}.$$

Die entsprechenden Zustandswahrscheinlichkeiten des MC–Modells sind $\alpha_{\rm G}$ und $\alpha_{\rm B}$.

Hinweise:

• Die Aufgabe gehört zum Kapitel Bündelfehlerkanäle.
• In der nachfolgenden Aufgabe 5.7Z werden die wichtigsten Beschreibungsgrößen wie
  • Fehlerkorrelationsfunktion,
  • Korrelationsdauer,
  • mittlere Fehlerwahrscheinlichkeit und
  • Fehlerabstandsverteilung

direkt aus den MC–Parametern berechnet.

Fragebogen

1

Berechnen Sie die folgenden Hilfsgrößen:

$u_{\rm GG}\hspace{0.05cm} = \ $

$u_{\rm BG}\ = \ $

$u_{\rm GB}\ = \ $

$u_{\rm BB}\ = \ $

$\beta_{\rm G}\hspace{0.3cm} = \ $

$\beta_{\rm B}\hspace{0.32cm} = \ $

2

Wie lauten die beiden Fehlerwahrscheinlichkeiten des MC–Modells?

$q_{\rm G} \hspace{0.08cm} = \ $

$q_{\rm B} \ = \ $

3

Berechnen Sie die weiteren Hilfsgrößen:

$x_{\rm G} \ = \ $

$x_{\rm B} \ = \ $

$\alpha_{\rm G} \hspace{0.05cm} = \ $

$\alpha_{\rm B} \ = \ $

4

Berechnen Sie die Übergangswahrscheinlichkeiten des MC–Modells:

$q(\rm B\hspace{0.05cm}|\hspace{0.05cm} G)\ = \ $

$q(\rm G\hspace{0.05cm}|\hspace{0.05cm} B)\ = \ $

Musterlösung

Solution

(1)  Für die $u$–Hilfsgrößen gilt:

$$u_{\rm GG} \hspace{-0.1cm} \ = \ \hspace{-0.1cm}{\rm Pr}(\rm G\hspace{0.05cm}|\hspace{0.05cm} G ) \cdot (1-{\it p}_{\rm G}) = 0.99 \cdot (1 -0.001) \hspace{0.15cm}\underline {\approx 0.98901} \hspace{0.05cm},$$

$$u_{\rm BG} \hspace{-0.1cm} \ = \ \hspace{-0.1cm}{\rm Pr}(\rm G\hspace{0.05cm}|\hspace{0.05cm} B ) \cdot (1-{\it p}_{\rm B})= 0.1 \cdot (1 -0.1) \hspace{0.15cm}\underline {\approx 0.09} \hspace{0.05cm},$$

$$u_{\rm GB} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {\rm Pr}(\rm B\hspace{0.05cm}|\hspace{0.05cm} G ) \cdot (1-{\it p}_{\rm G})= 0.01 \cdot (1 -0.001) \hspace{0.15cm}\underline {\approx 0.00999} \hspace{0.05cm},$$

$$u_{\rm BB} \hspace{-0.1cm} \ = \ \hspace{-0.1cm}{\rm Pr}(\rm B\hspace{0.05cm}|\hspace{0.05cm} B ) \cdot (1-{\it p}_{\rm B})= 0.9 \cdot (1 -0.1) \hspace{0.15cm}\underline {\approx 0.81}\hspace{0.05cm}.$$

Daraus folgt für die $\beta$–Hilfsgrößen:

$$\beta_{\rm G} =\frac{u_{\rm GG} + u_{\rm BB} + \sqrt{(u_{\rm GG} - u_{\rm BB})^2 + 4 \cdot u_{\rm GB}\cdot u_{\rm BG}}}{2} =\frac{0.98901 + 0.81 + \sqrt{(0.98901 - 0.81)^2 + 4 \cdot 0.00999\cdot 0.09}}{2} $$

$$\Rightarrow \hspace{0.3cm}\beta_{\rm G}= \frac{1.79901 + \sqrt{0.03204 + 0.003596}}{2} = \frac{1.79901 + 0.18877}{2} \hspace{0.15cm}\underline {= 0.9939} \hspace{0.05cm},$$

$$\beta_{\rm B} \hspace{-0.1cm} \ = \ \hspace{-0.1cm}\frac{u_{\rm GG} + u_{\rm BB} - \sqrt{(u_{\rm GG} - u_{\rm BB})^2 + 4 \cdot u_{\rm GB}\cdot u_{\rm BG}}}{2}\hspace{0.05cm}, = \ \hspace{-0.1cm}\text{...} = \frac{1.79901 - 0.18877}{2} \hspace{0.15cm}\underline {= 0.8051} \hspace{0.05cm}.$$

(2)  Mit dem Ergebnis der Teilaufgabe (1) erhält man:

$$q_{\rm G} = 1-\beta_{\rm G} = 1 - 0.9939 \hspace{0.15cm}\underline {= 0.0061}\hspace{0.05cm}, \hspace{0.3cm}q_{\rm B} = 1-\beta_{\rm B}= 1 - 0.8051 \hspace{0.15cm}\underline {= 0.1949}\hspace{0.05cm}.$$

(3)  Entsprechend dem Angabenblatt ist hier anzusetzen

$$x_{\rm G} \hspace{-0.1cm} \ = \ \hspace{-0.1cm}\frac{u_{\rm BG}}{\beta_{\rm G}-u_{\rm BB}}= \frac{0.0999}{0.9939-0.81}\hspace{0.15cm}\underline {= 0.5432}\hspace{0.05cm},$$

$$ x_{\rm B} \hspace{-0.1cm} \ = \ \hspace{-0.1cm}\frac{u_{\rm BG}}{\beta_{\rm B}-u_{\rm BB}}= \frac{0.0999}{0.8051-0.81}\hspace{0.15cm}\underline {= -20.388}\hspace{0.05cm},$$

$$\alpha_{\rm G} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \frac{(w_{\rm G} \cdot p_{\rm G} + w_{\rm B} \cdot p_{\rm B}\cdot x_{\rm G})( x_{\rm B}-1)}{p_{\rm M} \cdot( x_{\rm B}-x_{\rm G})} = \frac{(0.9091 \cdot 0.001 + 0.0909 \cdot 0.1\cdot 0.5432)( -20.388-1)}{0.01 \cdot( -20.388 -0.5432)} \hspace{0.15cm}\underline {= 0.5975} \hspace{0.05cm},$$

$$\alpha_{\rm B} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 1-\alpha_{\rm G} \hspace{0.15cm}\underline {= 0.4025}\hspace{0.05cm}.$$

(4)  Entsprechend den vorgegebenen Gleichungen gilt:

$$q(\rm B\hspace{0.05cm}|\hspace{0.05cm} G ) \hspace{-0.1cm} \ = \ \hspace{-0.1cm}\frac{\alpha_{\rm B} \cdot[{\rm Pr}(\rm B\hspace{0.05cm}|\hspace{0.05cm} G ) + {\rm Pr}(\rm G\hspace{0.05cm}|\hspace{0.05cm} B )]}{\alpha_{\rm G} \cdot q_{\rm B} + \alpha_{\rm B} \cdot q_{\rm G}} =\frac{0.4025 \cdot[0.1 + 0.01]}{0.5975 \cdot 0.1949 + 0.4025 \cdot 0.0061}\hspace{0.15cm}\underline {= 0.3724} \hspace{0.05cm},$$

$$q(\rm G\hspace{0.05cm}|\hspace{0.05cm} B ) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \frac{\alpha_{\rm G}}{\alpha_{\rm B}} \cdot q(\rm B\hspace{0.05cm}|\hspace{0.05cm} G )= \frac{0.5975}{0.4025} \cdot 0.3724 \hspace{0.15cm}\underline {= 0.5528}\hspace{0.05cm}.$$