Aufgaben:Exercise 2.1: Rectification

• Return to book

Periodisches Dreiecksignal

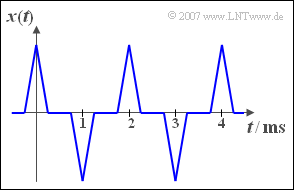
Die Grafik zeigt das periodische Signal $x(t)$. Legt man $x(t)$ an den Eingang einer Nichtlinearität mit der Kennlinie

$$y=g(x)=\left\{ {x \; \rm f\ddot{u}r\; \it x \geq \rm 0, \atop {\rm 0 \;\;\; \rm sonst,}}\right.$$

so erhält man am Ausgang das Signal $y(t)$. Eine zweite nichtlineare Kennlinie

$$z=h(x)=|x|$$

liefert das Signal $z(t)$.

Hinweis:

• Die Aufgabe gehört zum Kapitel Allgemeine Beschreibung periodischer Signale.

Fragebogen

1

Welche der folgenden Aussagen sind zutreffend?

	$y = g(x)$ beschreibt einen Einweggleichrichter.
	$y = g(x)$ beschreibt einen Zweiweggleichrichter.
	$z = h(x)$ beschreibt einen Einweggleichrichter.
	$z = h(x)$ beschreibt einen Zweiweggleichrichter

2

Wie groß ist die Grundfrequenz $f_0$ des Signals $x(t)$?

$f_0 \ = \ $   $\text{Hz}$

3

Wie groß ist die Periodendauer des Signals $y(t)$?

$T_0 \ = \ $   $\text{ms}$

4

Wie groß ist die Grundkreisfrequenz des Signals $z(t)$?

$\omega_0 \ = \ $   $\text{1/s}$

Musterlösung

Solution

(1)  Richtig sind die Lösungsvorschläge 1 und 4:

• Die nichtlineare Kennlinie $y = g(x)$ beschreibt einen Einweggleichrichter.
• $z = h(x) = |x|$ beschreibt einen Zweiweggleichrichter.

(2)  Die Periodendauer des gegebenen Signals $x(t)$ beträgt $T_0 = 2\,\text{ms}$ . Der Kehrwert hiervon ergibt die Grundfrequenz $f_0 \hspace{0.1cm}\underline{ = 500\,\text{Hz}}$.

(3)  Die Einweggleichrichtung ändert nichts an der Periodendauer, siehe linke Skizze. Somit gilt weiterhin $T_0 \hspace{0.1cm}\underline{= 2\,\text{ms}}$.

Periodische Dreiecksignale

(4)  Das Signal z(t) nach der Doppelweggleichrichtung hat dagegen die doppelte Frequenz (siehe rechte Darstellung). Hier gelten folgende Werte:

$$T_0 = 1\,\text{ms}, \hspace{0.5cm} f_0 = 1\,\text{kHz}, \hspace{0.5cm} \omega_0 \hspace{0.1cm}\underline{= 6283\,\text{1/s}}.$$