Aufgaben:Exercise 3.9Z: Sine Transformation

• Return to book

Eingangs–WDF und Kennlinie

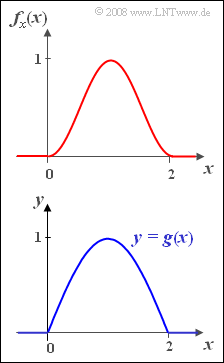
Wir betrachten in dieser Aufgabe eine Zufallsgröße $x$ mit $\sin^2$–förmiger WDF im Bereich zwischen $x= 0$ und $x= 2$:

$$f_x(x)= \sin^2({\rm\pi}/{\rm 2}\cdot x) \hspace{1cm}\rm f\ddot{u}r\hspace{0.15cm}{\rm 0\le \it x \le \rm 2} .$$

Außerhalb ist die WDF identisch $0$.

Der Mittelwert und die Streuung dieser Zufallsgröße $x$ wurden bereits in der Aufgabe 3.3 ermittelt:

$$m_x = 1,\hspace{0.2cm}\sigma_x = 0.361.$$

Eine weitere Zufallsgröße $y$ erhält man durch Transformation mittels der nichtlinearen Kennlinie

$$y= g(x) =\sin({\rm\pi}/{\rm 2}\cdot x).$$

Die Abbildung zeigt jeweils im Bereich $0 \le x \le 2$:

• oben die WDF $f_x(x)$,
• unten die nichtlineare Kennlinie $y = g(x)$.

Hinweise:

• Die Aufgabe gehört zum Kapitel Exponentialverteilte Zufallsgrößen.
• Besonderer Bezug genommen wird auf die Seite Transformation von Zufallsgrößen und auf das Kapitel Erwartungswerte und Momente.

• Vorgegeben sind die beiden unbestimmten Integrale:

$$\int \sin^{\rm 3}( ax)\,{\rm d}x = \frac{\rm 1}{ 3 a} \cdot \cos^{\rm 3}( ax)-\frac{\rm 1}{ a}\cdot \cos(ax),$$

$$\int \sin^{\rm 4}(ax)\,{\rm d}x =\frac{\rm 3}{\rm 8}\cdot x-\frac{\rm 1}{\rm 4 a} \cdot \sin(2 ax)+\frac{\rm 1}{32 a}\cdot \sin(4 ax).$$

Fragebogen

1

Welche der folgenden Aussagen sind zutreffend?

	$y$ ist auf den Wertbereich $0 \le y \le 1$ begrenzt.
	$y$ ist auf den Wertbereich $0 < y \le 1$ begrenzt.
	Der Mittelwert $m_y$ ist kleiner als der Mittelwert $m_x$.

2

Berechnen Sie den Mittelwert der Zufallsgröße $y$.

$m_y \ = \ $

3

Berechnen Sie den quadratischen Mittelwert von $y$ und die Streuung.

$\sigma_y \ = \ $

4

Berechnen Sie die WDF $f_y(y)$. Hinweis:   Beachten Sie die Symmetrieeigenschaften.
Welcher WDF–Wert ergibt sich für $y = 0.6$?

$f_y(y=0.6) \ = \ $

5

Welcher WDF-Wert ergibt sich für $y = 1$? Interpretieren Sie das Ergebnis.
Wie groß ist die Wahrscheinlichkeit, dass $y$ exakt gleich $1$ ist?

${\rm Pr}(y=1) \ = \ $

Musterlösung

Solution

(1)  Richtig sind der zweite und der dritte Lösungsvorschlag:

• Aufgrund des Wertebereichs von $x$ und der gegebenen Kennlinie kann $y$ keine Werte kleiner als $0$ bzw. größer als $1$ annehmen.
• Der Wert $y = 0$ kann allerdings ebenfalls nicht auftreten, da weder $x = 0$ noch $x = 2$ möglich sind.
• Mit diesen Eigenschaften ergibt sich sicher  $m_y < 1$, also ein kleinerer Wert als  $m_x = 1$ (siehe Angabe).

(2)  Zur Lösung dieser Aufgabe könnte man beispielsweise zunächst die WDF $f_y(y)$ bestimmen und daraus in gewohnter Weise  $m_y$ berechnen.
Zum gleichen Ergebnis führt der direkte Weg:

$$m_y={\rm E}\big[y\big]={\rm E}\big[g(x)\big]=\int_{-\infty}^{+\infty}g(x)\cdot f_x(x)\,{\rm d}x.$$

Mit den aktuellen Funktionen $g(x)$ und $f_x(x)$ erhält man:

$$m_y=\int_{\rm 0}^{\rm 2}\hspace{-0.1cm}\sin^{\rm 3}({\pi}/{ 2}\cdot x)\,{\rm d}x=\frac{\rm 2}{\rm 3\cdot \pi}\cdot \cos^{\rm 3}({\pi}/{ 2}\cdot x)-\frac{\rm 2}{\rm \pi} \cdot \cos({3 \rm \pi}/{\rm 2}\cdot x)\Big|_{\rm 0}^{\rm 2}=\frac{\rm 8}{\rm 3\cdot \pi} \hspace{0.15cm}\underline{=\rm 0.849}.$$

(3)  In Analogie zu Punkt (2) gilt:

$$m_{2 y}={\rm E}[y^{\rm 2}]={\rm E}[g^{\rm 2}( x)]=\int_{-\infty}^{+\infty}\hspace{-0.35cm}g^{2}( x)\cdot f_x(x)\,{\rm d}x.$$

Dies führt zum Ergebnis:

$$ m_{ 2 y}=\int_{\rm 0}^{\rm 2}\hspace{-0.15cm}\sin^{\rm 4}({\rm \pi}/{\rm 2}\cdot x)\,{\rm d} x= \frac{\rm 3}{\rm 8}\cdot x-\frac{\rm 1}{\rm 2\cdot\pi}\cdot \sin(\rm \pi\cdot{\it x})+\frac{\rm 1}{\rm 16\cdot\pi}\cdot \sin(\rm 2 \pi\cdot {\it x})\Big|_{\rm 0}^{\rm 2} \hspace{0.15cm}{= \rm 0.75}.$$

Mit dem Ergebnis aus (2) folgt somit für die Streuung:

$$ \sigma_{y}=\sqrt{\frac{\rm 3}{\rm 4}-\Big(\frac{\rm 8}{\rm 3\cdot\pi}\Big)^{\rm 2}} \hspace{0.15cm}\underline{\approx \rm 0.172}.$$

(4)  Aufgrund der Symmetrie von WDF $f_x(x)$ und Kennlinie $y =g(x)$ um $x = 1$ liefern die beiden Bereiche

• $0 \le x \le 1$ und
• $1 \le x \le 2$

jeweils den gleichen Beitrag für $f_y(y)$. Im ersten Bereich ist die Ableitung der Kennlinie positiv,

WDF nach Transformation

$$g\hspace{0.05cm}'(x)={\rm \pi}/{\rm 2}\cdot \cos({\rm \pi}/{\rm 2}\cdot x),$$

und die Umkehrfunktion lautet: $$ x=h(y)={\rm 2}/{\rm \pi}\cdot \arcsin( y).$$

Unter Berücksichtigung des zweiten Beitrags durch den Faktor $2$ erhält man für die gesuchte WDF im Bereich $0 \le y \le 1$ ):

$$f_y(y)= 2\cdot\frac{\sin^{ 2}({ \pi}/{ 2}\cdot x)}{{ \pi}/{ 2}\cdot \cos({ \pi}/{ 2}\cdot x)}\Big|_{\, x={ 2}/{ \pi}\cdot \arcsin( y)}.$$

Außerhalb ist $f_y(y) \equiv 0$. Dies führt zum Zwischenergebnis

$$f_y(y)=\frac{4}{\pi}\cdot \frac{\sin^{2}(\arcsin( y ))}{\sqrt{\rm 1-\sin^{ 2}(\arcsin( y \rm ))}},$$

und wegen $\sin(\arcsin(y)) = y$:

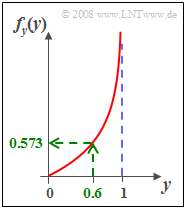
$$f_y(y)=\frac{ 4}{\pi}\cdot \frac{ y^{2}}{\sqrt{1- y^{\rm 2}}}.$$

• An der Stelle $y = 0.6$ erhält man den Wert $f_y(y= 0.6)\hspace{0.15cm}\underline{=0.573}$.
• Rechts ist diese WDF $f_y(y)$ grafisch dargestellt.

(5)  Die WDF ist an der Stelle $y = 1$ unendlich groß.

• Dies hängt damit zusammen, dass an dieser Stelle die Ableitung $g\hspace{0.05cm}'(x)$ der Kennlinie horizontal verläuft.
• Da aber $y$ eine kontinuierliche Zufallsgröße ist, gilt trotzdem ${\rm Pr}(y = 1) \hspace{0.15cm}\underline{= 0}$.

Das bedeutet:

• Eine Unendlichkeitsstelle in der WDF ist nicht identisch mit einer Diracfunktion.
• Oder salopper ausgedrückt: Eine Unendlichkeitsstelle in der WDF ist „weniger” als eine Diracfunktion.