Aufgaben:Exercise 4.1: Triangular (x, y) Area

• Return to book

Dreieckigförmiges 2D-Gebiet

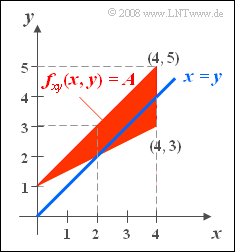
Eine 2D-Zufallsgröße ist durch die nebenstehende Skizze definiert:

• Für ($x$, $y$) können nur Werte innerhalb des durch die drei Eckpunkte $(0,\ 1)$, $(4,\ 3)$ und $(4,\ 5)$ festgelegten dreieckförmigen Gebietes auftreten.
• Innerhalb des Dreiecks sind alle Zufallsgrößen $(x, \ y)$ gleichwahrscheinlich.
• Für die 2D–WDF gilt somit:

$$f_{xy}(x,y) = A .$$

Zusätzlich ist die Gerade $x = y$   ⇒   „Winkelhalbierende” in obiger Skizze eingezeichnet   ⇒  siehe Teilaufgabe (2).

Hinweis:

• Die Aufgabe gehört zum Kapitel Zweidimensionale Zufallsgrößen.

Fragebogen

1

Bestimmen Sie die WDF–Konstante anhand geometrischer Überlegungen.

$A \ = \ $

2

Berechnen Sie die Wahrscheinlichkeit, dass $x$ größer als $y$ ist.

${\rm Pr}(x > y) \ = \ $

3

Ermitteln Sie die Rand–WDF $f_x(x)$. Berechnen Sie die Wahrscheinlichkeit, dass $x$ größer oder gleich $2$ ist.
Überprüfen Sie den Wert anhand der 2D–WDF.

${\rm Pr}(x ≥ 2)\ = \ $

4

Ermitteln Sie die Rand–WDF $f_y(y)$. Berechnen Sie die Wahrscheinlichkeit, dass $y$ größer oder gleich $3$ ist.
Überprüfen Sie den Wert anhand der 2D–WDF.

${\rm Pr}(y ≥ 3)\ = \ $

5

Wie groß ist die Wahrscheinlichkeit, dass die Zufallsgröße $x$ größer oder gleich $2$ und gleichzeitig die Zufallsgröße $y$ größer oder gleich $3$ ist?

${\rm Pr}\big[(x ≥ 2) ∩ (y ≥ 3)\big]\ = \ $

6

Wie groß ist die Wahrscheinlichkeit, dass $x$ größer oder gleich $2$ ist, unter der Bedingung, dass $y \ge 3$ gilt?

${\rm Pr}\big[x ≥ 2\hspace{0.05cm} | \hspace{0.05cm} y ≥ 3\big]\ = \ $

7

Wie groß ist die Wahrscheinlichkeit, dass $y \ge 3$ ist, unter der Bedingung, dass $x \ge 2$ gilt?

${\rm Pr}\big[y ≥ 3\hspace{0.05cm} | \hspace{0.05cm} x ≥ 2\big]\ = \ $

Musterlösung

Solution

(1)  Das Volumen unter der zweidimensionalen WDF ist definitionsgemäß gleich $1$: $$\int_{-\infty}^{+\infty}\int_{-\infty}^{+\infty}f_{xy}(x,y)\, {\rm d}x\, {\rm d}y=1.$$

Die Dreiecksfläche ist $D = 0.5 \cdot 2 \cdot 4 = 4$. Da in diesem Definitionsgebiet die WDF konstant gleich $A$ ist, erhält man $A= 1/D\hspace{0.15cm}\underline{= 0.25}$.

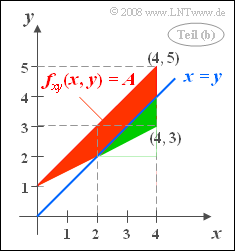
(2)  Zur Lösung gehen wir von nebenstehender Skizze aus. Das Gebiet $x>y$ liegt rechts von der Winkelhalbierenden $x=y$ und ist grün markiert.

Diese grüne Dreiecksfläche ist $D_{rm (2)} = 0.5 \cdot 1 \cdot 2 = 1 $, also genau ein Viertel der Gesamtfläche $D$ des Definitionsgebietes. Daraus folgt ${\rm Pr}(x > y)\hspace{0.15cm}\underline{= 0.25}$.

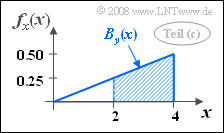
(3)  Für die gesuchte Rand-WDF gilt in diesem Fall: $$f_x(x)=\int_{-\infty}^{+\infty}f_{xy}(x,y)\, {\rm d}y=A\cdot B_y (x).$$

Hierbei bezeichnet $B_y(x)$ die Breite des Gebietes $f_{xy} \ne 0$ in $y$-Richtung beim betrachteten $x$-Wert. Es gilt: $B_y(x) = x/2$. Mit $A = 0.25$ folgt $f_{x}(x) = x/8$ für den Bereich $ 0 \le x \le 4$.

Die gesuchte Wahrscheinlichkeit entspricht der schraffierten Fläche in nebenstehender Skizze. Man erhält: $$\rm Pr(\it x\ge \rm 2) = \rm 1-\rm Pr(\it x < \rm 2) = \rm 1-\frac{1}{2}\cdot2\cdot 0.25\hspace{0.15cm}\underline{ =0.75}. $$

Zum gleichen Ergebnis gelangt man anhand der 2D-WDF: Rechts von der Senkrechten $x = 2$ liegt $3/4$ des gesamten Definitionsgebiets.

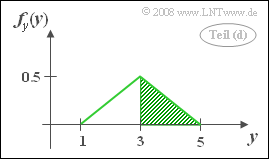
(4)  Analog der Musterlösung der Teilaufgabe (3) gilt: $$f_y(y)=\int_{-\infty}^{+\infty}f_{xy}(x,y)\, {\rm d}x=A\cdot B_x (y).$$

Die Ausbreitung des WDF-Gebietes in $x$-Richtung ist für $y \le 1$ und $y \ge 5$ jeweils $0$. Das Maximum liegt bei $y=3$ und ergibt $B_x(y=3) = 2$. Dazwischen ist die Zu– und Abnahme von $B_x(y)$ linear und es ergibt sich eine dreieckförmige WDF.

Die Wahrscheinlichkeit, dass $y \ge 3$ ist, entspricht der grün schraffierten Fläche in der nebenstehenden Skizze und ergibt aufgrund der Symmetrie $${\rm Pr}(y ≥ 3)\hspace{0.15cm}\underline{ =0.5}. $$

Zum gleichen Ergebnis kommt man anhand der 2D–WDF: Oberhalb der Horizontalen $y= 3$ liegt die Hälfte des gesamten Definitionsgebietes.

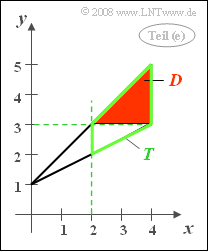
(5)  Wenn $y \ge 3$ ist (rot hinterlegtes Dreieck $D$), gilt stets auch $x \ge 2$ (grün umrandetes Trapez T). Das bedeutet: In diesem Beispiel ist $D$ eine Teilmenge von $T$, und es gilt: $${\rm Pr}[(x ≥ 2) ∩ (y ≥ 3)] = {\rm Pr}(y ≥ 3) \hspace{0.15cm}\underline{= 0.50}.$$

(6)  Entsprechend der Lösung zur letzten Teilaufgabe (e) folgt aus $y \ge 3$ mit Sicherheit auch$x \ge 2$“. Somit ist die gesuchte bedingte Wahrscheinlichkeit: $${\rm Pr}[x ≥ 2\hspace{0.05cm} | \hspace{0.05cm} y ≥ 3]\hspace{0.15cm}\underline{= 1}.$$

(7)  Diese Teilaufgabe kann man mit dem Satz von Bayes und den Ergebnissen aus (2) und (5) und lösen: $$\rm Pr(\it y \ge \rm 3\hspace{0.1cm}|\hspace{0.1cm} \it x \ge \rm 2) = \frac{ \rm Pr((\it x \ge \rm 2)\cap(\it y \ge \rm 3))} {\rm Pr(\it x \ge \rm 2)}\hspace{0.15cm}\underline{=\rm {2}/{3}}.$$

Oder anders ausgedrückt: Die Fläche $D$ des rot hinterlegten Dreiecks macht $2/3$ der Fläche des grün umrandeten Trapezes $T$ aus.