Difference between revisions of "Theory of Stochastic Signals/Linear Combinations of Random Variables"
| Line 7: | Line 7: | ||
==Voraussetzungen und Mittelwerte== | ==Voraussetzungen und Mittelwerte== | ||
<br> | <br> | ||
| − | + | Im gesamten Kapitel „ Linearkombinationen von Zufallsgrößen ” gehen wir von den folgenden Annahmen aus: | |
*Die Zufallsgrößen $u$ und $v$ seien jeweils mittelwertfrei ⇒ $m_u = m_v = 0$ und zudem statistisch unabhängig voneinander ⇒ $ρ_{uv} = 0$. | *Die Zufallsgrößen $u$ und $v$ seien jeweils mittelwertfrei ⇒ $m_u = m_v = 0$ und zudem statistisch unabhängig voneinander ⇒ $ρ_{uv} = 0$. | ||
*Die beiden Zufallsgrößen $u$ und $v$ besitzen jeweils gleiche Streuung $σ$. Über die Art der Verteilung wird keine Aussage getroffen. | *Die beiden Zufallsgrößen $u$ und $v$ besitzen jeweils gleiche Streuung $σ$. Über die Art der Verteilung wird keine Aussage getroffen. | ||
| Line 21: | Line 21: | ||
==Resultierender Korrelationskoeffizient== | ==Resultierender Korrelationskoeffizient== | ||
<br> | <br> | ||
| − | Betrachten wir nun die '''Varianzen''' der Zufallsgrößen nach den Linearkombinationen. Für die Zufallsgröße $x$ gilt unabhängig vom Parameter $C$: | + | Betrachten wir nun die '''Varianzen''' der Zufallsgrößen nach den Linearkombinationen. |
| − | :$$\sigma _x ^2 = {\rm E}[x ^{\rm 2}] = A^{\rm 2} \cdot {\rm E}[u^{\rm 2}] + B^{\rm 2} \cdot {\rm E}[v^{\rm 2}] + {\rm 2} \cdot A \cdot B \cdot {\rm E}[u \cdot v].$$ | + | *Für die Zufallsgröße $x$ gilt unabhängig vom Parameter $C$: |
| + | :$$\sigma _x ^2 = {\rm E}\big[x ^{\rm 2}\big] = A^{\rm 2} \cdot {\rm E}\big[u^{\rm 2}\big] + B^{\rm 2} \cdot {\rm E}\big[v^{\rm 2}\big] + {\rm 2} \cdot A \cdot B \cdot {\rm E}\big[u \cdot v\big].$$ | ||
| − | Die Erwartungswerte von $u^2$ und $v^2$ sind definitionsgemäß jeweils gleich $σ^2$, weil $u$ und $v$ mittelwertfrei sind. Da $u$ und $v$ zudem als statistisch unabhängig vorausgesetzt werden, kann man für den Erwartungswert des Produktes auch schreiben: | + | *Die Erwartungswerte von $u^2$ und $v^2$ sind definitionsgemäß jeweils gleich $σ^2$, weil $u$ und $v$ mittelwertfrei sind. |
| − | :$${\rm E}[u \cdot v] = {\rm E}[u] \cdot {\rm E}[v] = m_u \cdot m_v = \rm 0.$$ | + | *Da $u$ und $v$ zudem als statistisch unabhängig vorausgesetzt werden, kann man für den Erwartungswert des Produktes auch schreiben: |
| − | Damit erhält man für die Varianzen der durch Linearkombinationen gebildeten Zufallsgrößen: | + | :$${\rm E}\big[u \cdot v\big] = {\rm E}\big[u\big] \cdot {\rm E}\big[v\big] = m_u \cdot m_v = \rm 0.$$ |
| + | *Damit erhält man für die Varianzen der durch Linearkombinationen gebildeten Zufallsgrößen: | ||
:$$\sigma _x ^2 =(A^2 + B^2) \cdot \sigma ^2,$$ | :$$\sigma _x ^2 =(A^2 + B^2) \cdot \sigma ^2,$$ | ||
:$$\sigma _y ^2 =(D^2 + E^2) \cdot \sigma ^2.$$ | :$$\sigma _y ^2 =(D^2 + E^2) \cdot \sigma ^2.$$ | ||
| Line 32: | Line 34: | ||
Die '''Kovarianz''' $μ_{xy}$ ist bei mittelwertfreien Zufallsgrößen $x$ und $y$ ⇒ $C = F = 0$ identisch mit dem gemeinsamen Moment $m_{xy}$: | Die '''Kovarianz''' $μ_{xy}$ ist bei mittelwertfreien Zufallsgrößen $x$ und $y$ ⇒ $C = F = 0$ identisch mit dem gemeinsamen Moment $m_{xy}$: | ||
| − | :$$\mu_{xy } = m_{xy } = {\rm E}[x \cdot y] = {\rm E}[(A \cdot u + B \cdot v)(D \cdot u + E \cdot v)].$$ | + | :$$\mu_{xy } = m_{xy } = {\rm E}\big[x \cdot y\big] = {\rm E}\big[(A \cdot u + B \cdot v)(D \cdot u + E \cdot v)\big].$$ |
| − | Beachten Sie hierbei, dass ${\rm E}[ \text{...} ]$ einen Erwartungswert bezeichnet, während $E$ eine Variable beschreibt. Nach Auswertung dieser Gleichung in analoger Weise zu oben folgt daraus: | + | Beachten Sie hierbei, dass ${\rm E}\big[ \text{...} \big]$ einen Erwartungswert bezeichnet, während $E$ eine Variable beschreibt. |
| + | |||
| + | {{BlaueBox|TEXT= | ||
| + | $\text{Fazit:}$ Nach Auswertung dieser Gleichung in analoger Weise zu oben folgt daraus: | ||
:$$\mu_{xy } = (A \cdot D + B \cdot E) \cdot \sigma^{\rm 2 } | :$$\mu_{xy } = (A \cdot D + B \cdot E) \cdot \sigma^{\rm 2 } | ||
\hspace{0.3cm}\Rightarrow\hspace{0.3cm} | \hspace{0.3cm}\Rightarrow\hspace{0.3cm} | ||
| − | \rho_{xy } = \frac{\rho_{xy }}{\sigma_x \cdot \sigma_y} = \frac {A \cdot D + B \cdot E}{\sqrt{(A^{\rm 2}+B^{\rm 2})(D^{\rm 2}+E^{\rm 2})}}. $$ | + | \rho_{xy } = \frac{\rho_{xy } }{\sigma_x \cdot \sigma_y} = \frac {A \cdot D + B \cdot E}{\sqrt{(A^{\rm 2}+B^{\rm 2})(D^{\rm 2}+E^{\rm 2} ) } }. $$}} |
| + | |||
| − | + | Wir schließen nun die Sonderfälle $A = B = 0$ (d. h. $x ≡ 0$ ) sowie $D = E = 0$ (d. h. $y ≡ 0$ ) aus. Dann liefert diese Gleichung stets eindeutige Werte für den Korrelationskoeffizienten im Bereich $–1 ≤ ρ_{xy} ≤ +1$. | |
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
| Line 45: | Line 51: | ||
*Nun hängt $x$ nur noch von $v$ und $y$ ausschließlich von $u$ ab. | *Nun hängt $x$ nur noch von $v$ und $y$ ausschließlich von $u$ ab. | ||
*Da aber $u$ und $v$ als statistisch unabhängig angenommen wurden, bestehen keine Beziehungen zwischen $x$ und $y$. | *Da aber $u$ und $v$ als statistisch unabhängig angenommen wurden, bestehen keine Beziehungen zwischen $x$ und $y$. | ||
| − | *Ebenso ergibt sich $ρ_{xy} = 0$ für die Kombination $B = D = 0$.}} | + | *Ebenso ergibt sich $ρ_{xy} = 0$ für die Kombination $B = D = 0$.}} |
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
| − | $\text{Beispiel 2:}$ Die Konstellation $B = E = 0$ führt dazu, dass sowohl $x$ als auch $y$ nur noch von $u$ abhängen. | + | $\text{Beispiel 2:}$ Die Konstellation $B = E = 0$ führt dazu, dass sowohl $x$ als auch $y$ nur noch von $u$ abhängen. Dann ergibt sich für den Korrelationskoeffizienten: |
:$$\rho_{xy } = \frac {A \cdot D }{\sqrt{A^{\rm 2}\cdot D^{\rm 2} } } = \frac {A \cdot D }{\vert A\vert \cdot \vert D\vert } =\pm 1. $$ | :$$\rho_{xy } = \frac {A \cdot D }{\sqrt{A^{\rm 2}\cdot D^{\rm 2} } } = \frac {A \cdot D }{\vert A\vert \cdot \vert D\vert } =\pm 1. $$ | ||
*Besitzen $A$ und $D$ gleiches Vorzeichen, so ist $ρ_{xy} = +1$. | *Besitzen $A$ und $D$ gleiches Vorzeichen, so ist $ρ_{xy} = +1$. | ||
*Bei unterschiedlichen Vorzeichen ergibt sich der Korrelationskoeffizient $-1$. | *Bei unterschiedlichen Vorzeichen ergibt sich der Korrelationskoeffizient $-1$. | ||
| − | *Auch für $A = D = 0$ ergibt sich der Koeffizient $ρ_{xy} = ±1$. }} | + | *Auch für $A = D = 0$ ergibt sich der Koeffizient $ρ_{xy} = ±1$, wenn $B \ne 0$ und $E \ne 0$ gilt. }} |
==Erzeugung korrelierter Zufallsgrößen== | ==Erzeugung korrelierter Zufallsgrößen== | ||
| Line 60: | Line 66: | ||
Die [[Stochastische_Signaltheorie/Linearkombinationen_von_Zufallsgrößen#Resultierender_Korrelationskoeffizient|Gleichungen der letzten Seite]] können zur Erzeugung einer zweidimensionalen Zufallsgröße $(x, y)$ mit vorgegebenen Kenngrößen $σ_x$, $σ_y$ und $ρ_{xy}$ genutzt werden. | Die [[Stochastische_Signaltheorie/Linearkombinationen_von_Zufallsgrößen#Resultierender_Korrelationskoeffizient|Gleichungen der letzten Seite]] können zur Erzeugung einer zweidimensionalen Zufallsgröße $(x, y)$ mit vorgegebenen Kenngrößen $σ_x$, $σ_y$ und $ρ_{xy}$ genutzt werden. | ||
| − | *Werden außer diesen drei Sollwerten keine weiteren Voraussetzungen getroffen, so ist einer der vier Koeffizienten $A, B, D$ und $E$ frei wählbar. Im Folgenden wird stets willkürlich $E = 0$ gesetzt. | + | *Werden außer diesen drei Sollwerten keine weiteren Voraussetzungen getroffen, so ist einer der vier Koeffizienten $A, B, D$ und $E$ frei wählbar. |
| + | *Im Folgenden wird stets willkürlich $E = 0$ gesetzt. | ||
*Mit der weiteren Festlegung, dass die statistisch unabhängigen Zufallsgrößen $u$ und $v$ jeweils die Streuung $σ =1$ aufweisen, erhält man: | *Mit der weiteren Festlegung, dass die statistisch unabhängigen Zufallsgrößen $u$ und $v$ jeweils die Streuung $σ =1$ aufweisen, erhält man: | ||
:$$D = \sigma_y, \hspace{0.5cm} A = \sigma_x \cdot \rho_{xy}, \hspace{0.5cm} B = \sigma_x \cdot \sqrt {1-\rho_{xy}^2}.$$ | :$$D = \sigma_y, \hspace{0.5cm} A = \sigma_x \cdot \rho_{xy}, \hspace{0.5cm} B = \sigma_x \cdot \sqrt {1-\rho_{xy}^2}.$$ | ||
| Line 70: | Line 77: | ||
Wir gehen stets von mittelwertfreien Gaußschen Zufallsgrößen $u$ und $v$ aus. Beide besitzen die Varianz $σ^2 = 1$. | Wir gehen stets von mittelwertfreien Gaußschen Zufallsgrößen $u$ und $v$ aus. Beide besitzen die Varianz $σ^2 = 1$. | ||
| − | + | $(1)$ Zur Erzeugung einer 2D–Zufallsgröße mit den gewünschten Kennwerten $σ_x =1$, $σ_y = 1.55$ und $ρ_{xy} = -0.8$ eignet sich zum Beispiel der Parametersatz | |
| − | *Die Korrelationsgerade $K(x)$ ist rot dargestellt. Sie verläuft unter einem Winkel von etwa $-50^\circ$. | + | [[File:P_ID419__Sto_T_4_3_S3_neu.png|right |frame| Per Linearkombination erzeugte 2D-Zufallsgrößen]] |
| + | :$$A = -0.8, \; B = 0.6, \; D = 1.55, E = 0.$$ | ||
| + | *Dieser Parametersatz liegt der linken Grafik zugrunde. | ||
| + | *Die Korrelationsgerade $K(x)$ ist rot dargestellt. | ||
| + | *Sie verläuft unter einem Winkel von etwa $-50^\circ$. | ||
*Violett eingezeichnet ist die Ellipsenhauptachse, die etwas oberhalb der Korrelationsgeraden liegt. | *Violett eingezeichnet ist die Ellipsenhauptachse, die etwas oberhalb der Korrelationsgeraden liegt. | ||
| − | |||
| − | + | $(2)$ Der Parametersatz für die rechte Grafik lautet: | |
| + | :$$A = -0.625, B = 0.781, D = 1.501, E = -0.390.$$ | ||
*Im statistischen Sinne erhält man das gleiche Resultat, auch wenn sich die beiden Punktwolken im Detail unterscheiden. | *Im statistischen Sinne erhält man das gleiche Resultat, auch wenn sich die beiden Punktwolken im Detail unterscheiden. | ||
| − | *Insbesondere ergibt sich bezüglich Korrelationsgerade und Ellipsenhauptachse kein Unterschied zum Parametersatz | + | *Insbesondere ergibt sich bezüglich Korrelationsgerade und Ellipsenhauptachse kein Unterschied zum Parametersatz $(1)$. }} |
==Aufgaben zum Kapitel== | ==Aufgaben zum Kapitel== | ||
Revision as of 09:15, 17 August 2018
Contents
Voraussetzungen und Mittelwerte
Im gesamten Kapitel „ Linearkombinationen von Zufallsgrößen ” gehen wir von den folgenden Annahmen aus:
- Die Zufallsgrößen $u$ und $v$ seien jeweils mittelwertfrei ⇒ $m_u = m_v = 0$ und zudem statistisch unabhängig voneinander ⇒ $ρ_{uv} = 0$.
- Die beiden Zufallsgrößen $u$ und $v$ besitzen jeweils gleiche Streuung $σ$. Über die Art der Verteilung wird keine Aussage getroffen.
- Die beiden Zufallsgrößen $x$ und $y$ seien Linearkombinationen von $u$ und $v$, wobei gilt:
- $$x=A \cdot u + B \cdot v + C,$$
- $$y=D \cdot u + E \cdot v + F.$$
Für die (linearen) Mittelwerte der neuen Zufallsgrößen $x$ und $y$ erhält man nach den allgemeinen Rechenregeln für Erwartungswerte:
- $$m_x =A \cdot m_u + B \cdot m_v + C =C,$$
- $$m_y =D \cdot m_u + E \cdot m_v + F =F.$$
Die Koeffizienten $C$ und $F$ geben somit lediglich die Mittelwerte von $x$ und $y$ an. Beide werden auf den folgenden Seiten stets zu $0$ gesetzt.
Resultierender Korrelationskoeffizient
Betrachten wir nun die Varianzen der Zufallsgrößen nach den Linearkombinationen.
- Für die Zufallsgröße $x$ gilt unabhängig vom Parameter $C$:
- $$\sigma _x ^2 = {\rm E}\big[x ^{\rm 2}\big] = A^{\rm 2} \cdot {\rm E}\big[u^{\rm 2}\big] + B^{\rm 2} \cdot {\rm E}\big[v^{\rm 2}\big] + {\rm 2} \cdot A \cdot B \cdot {\rm E}\big[u \cdot v\big].$$
- Die Erwartungswerte von $u^2$ und $v^2$ sind definitionsgemäß jeweils gleich $σ^2$, weil $u$ und $v$ mittelwertfrei sind.
- Da $u$ und $v$ zudem als statistisch unabhängig vorausgesetzt werden, kann man für den Erwartungswert des Produktes auch schreiben:
- $${\rm E}\big[u \cdot v\big] = {\rm E}\big[u\big] \cdot {\rm E}\big[v\big] = m_u \cdot m_v = \rm 0.$$
- Damit erhält man für die Varianzen der durch Linearkombinationen gebildeten Zufallsgrößen:
- $$\sigma _x ^2 =(A^2 + B^2) \cdot \sigma ^2,$$
- $$\sigma _y ^2 =(D^2 + E^2) \cdot \sigma ^2.$$
Die Kovarianz $μ_{xy}$ ist bei mittelwertfreien Zufallsgrößen $x$ und $y$ ⇒ $C = F = 0$ identisch mit dem gemeinsamen Moment $m_{xy}$:
- $$\mu_{xy } = m_{xy } = {\rm E}\big[x \cdot y\big] = {\rm E}\big[(A \cdot u + B \cdot v)(D \cdot u + E \cdot v)\big].$$
Beachten Sie hierbei, dass ${\rm E}\big[ \text{...} \big]$ einen Erwartungswert bezeichnet, während $E$ eine Variable beschreibt.
$\text{Fazit:}$ Nach Auswertung dieser Gleichung in analoger Weise zu oben folgt daraus:
- $$\mu_{xy } = (A \cdot D + B \cdot E) \cdot \sigma^{\rm 2 } \hspace{0.3cm}\Rightarrow\hspace{0.3cm} \rho_{xy } = \frac{\rho_{xy } }{\sigma_x \cdot \sigma_y} = \frac {A \cdot D + B \cdot E}{\sqrt{(A^{\rm 2}+B^{\rm 2})(D^{\rm 2}+E^{\rm 2} ) } }. $$
Wir schließen nun die Sonderfälle $A = B = 0$ (d. h. $x ≡ 0$ ) sowie $D = E = 0$ (d. h. $y ≡ 0$ ) aus. Dann liefert diese Gleichung stets eindeutige Werte für den Korrelationskoeffizienten im Bereich $–1 ≤ ρ_{xy} ≤ +1$.
$\text{Beispiel 1:}$ Setzen wir zum Beispiel $A = E = 0$, so ergibt sich der Korrelationskoeffizient $ρ_{xy} = 0$. Dieses Ergebnis ist einsichtig:
- Nun hängt $x$ nur noch von $v$ und $y$ ausschließlich von $u$ ab.
- Da aber $u$ und $v$ als statistisch unabhängig angenommen wurden, bestehen keine Beziehungen zwischen $x$ und $y$.
- Ebenso ergibt sich $ρ_{xy} = 0$ für die Kombination $B = D = 0$.
$\text{Beispiel 2:}$ Die Konstellation $B = E = 0$ führt dazu, dass sowohl $x$ als auch $y$ nur noch von $u$ abhängen. Dann ergibt sich für den Korrelationskoeffizienten:
- $$\rho_{xy } = \frac {A \cdot D }{\sqrt{A^{\rm 2}\cdot D^{\rm 2} } } = \frac {A \cdot D }{\vert A\vert \cdot \vert D\vert } =\pm 1. $$
- Besitzen $A$ und $D$ gleiches Vorzeichen, so ist $ρ_{xy} = +1$.
- Bei unterschiedlichen Vorzeichen ergibt sich der Korrelationskoeffizient $-1$.
- Auch für $A = D = 0$ ergibt sich der Koeffizient $ρ_{xy} = ±1$, wenn $B \ne 0$ und $E \ne 0$ gilt.
Erzeugung korrelierter Zufallsgrößen
Die Gleichungen der letzten Seite können zur Erzeugung einer zweidimensionalen Zufallsgröße $(x, y)$ mit vorgegebenen Kenngrößen $σ_x$, $σ_y$ und $ρ_{xy}$ genutzt werden.
- Werden außer diesen drei Sollwerten keine weiteren Voraussetzungen getroffen, so ist einer der vier Koeffizienten $A, B, D$ und $E$ frei wählbar.
- Im Folgenden wird stets willkürlich $E = 0$ gesetzt.
- Mit der weiteren Festlegung, dass die statistisch unabhängigen Zufallsgrößen $u$ und $v$ jeweils die Streuung $σ =1$ aufweisen, erhält man:
- $$D = \sigma_y, \hspace{0.5cm} A = \sigma_x \cdot \rho_{xy}, \hspace{0.5cm} B = \sigma_x \cdot \sqrt {1-\rho_{xy}^2}.$$
- Bei $σ ≠ 1$ sind diese Werte jeweils noch durch $σ$ zu dividieren.
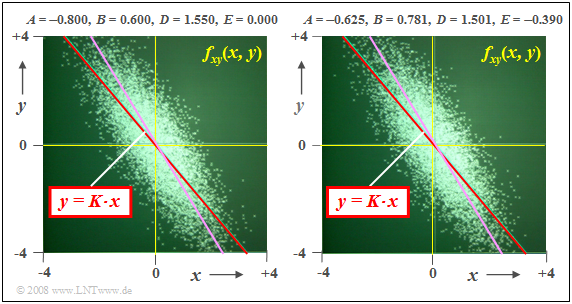
$\text{Beispiel 3:}$ Wir gehen stets von mittelwertfreien Gaußschen Zufallsgrößen $u$ und $v$ aus. Beide besitzen die Varianz $σ^2 = 1$.
$(1)$ Zur Erzeugung einer 2D–Zufallsgröße mit den gewünschten Kennwerten $σ_x =1$, $σ_y = 1.55$ und $ρ_{xy} = -0.8$ eignet sich zum Beispiel der Parametersatz
- $$A = -0.8, \; B = 0.6, \; D = 1.55, E = 0.$$
- Dieser Parametersatz liegt der linken Grafik zugrunde.
- Die Korrelationsgerade $K(x)$ ist rot dargestellt.
- Sie verläuft unter einem Winkel von etwa $-50^\circ$.
- Violett eingezeichnet ist die Ellipsenhauptachse, die etwas oberhalb der Korrelationsgeraden liegt.
$(2)$ Der Parametersatz für die rechte Grafik lautet:
- $$A = -0.625, B = 0.781, D = 1.501, E = -0.390.$$
- Im statistischen Sinne erhält man das gleiche Resultat, auch wenn sich die beiden Punktwolken im Detail unterscheiden.
- Insbesondere ergibt sich bezüglich Korrelationsgerade und Ellipsenhauptachse kein Unterschied zum Parametersatz $(1)$.
Aufgaben zum Kapitel
Aufgabe 4.7: Gewichtete Summe und Differenz
Aufgabe 4.7Z: Erzeugung einer 2D–WDF
Aufgabe 4.8: Rautenförmige 2D-WDF