Difference between revisions of "Applets:Bessel Functions of the First Kind"
| Line 75: | Line 75: | ||
<br><br> | <br><br> | ||
| − | === | + | ===Applications of the Bessel Functions=== |
| − | + | The applications of the Bessel functions in nature–and engineering are diverse and play an important role in physics, for example: | |
| − | * | + | * Examination of natural vibrations of cylindrical resonators, |
| − | * | + | * Solution of the radial Schrödinger-equation, |
| − | * | + | * Sound pressure amplitudes of low-viscosity rotational flows, |
| − | * | + | * Heat conduction in cylindrical bodies, |
| − | * | + | * Scattering problem of a grid, |
| − | * | + | * Dynamics of oscillating bodies, |
| − | * | + | * Angular resolution. |
| − | + | The Bessel functions are counted among the special functions because of their many applications in mathematical physics. | |
| − | + | In the following, we restrict ourselves to a few areas that are addressed in our tutorial $\rm LNTwww$. | |
| − | ''' | + | '''In the English original''' |
Electromagnetic waves in a cylindrical waveguide | Electromagnetic waves in a cylindrical waveguide | ||
Pressure amplitudes of inviscid rotational flows | Pressure amplitudes of inviscid rotational flows | ||
| Line 101: | Line 101: | ||
Dynamics of floating bodies | Dynamics of floating bodies | ||
Angular resolution | Angular resolution | ||
| − | '''Ende''' | + | '''The Ende''' |
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
| − | $\text{ | + | $\text{Example (C):} \hspace{0.5cm} \text{Use in spectral analysis} \ \Rightarrow \ \text{Kaiser-Bessel filter}$ |
| − | + | The '''spectral leakage effect''' is the falsification of the spectrum of a periodic and hence temporally unlimited signal due to the implicit time limitation of the discrete Fourier transform (DFT). This will be done, for example, by a spectrum analyzer | |
| − | * | + | * in the time signal not existing frequency components simulated, and / or |
| − | * | + | * actually existing spectral components are obscured by sidelobes. |
| − | + | The task of the [[Signaldarstellung/Spektralanalyse|spectral analysis]] is to limit the influence of the ''spectral leakage effect'' by providing suitable window functions. | |
| − | + | Such a window function provides, for example, the Kaiser–Bessel–window ⇒ see section [[Signaldarstellung/Spektralanalyse#Spezielle_Fensterfunktionen|Special Window Functions]]. Its time-discrete Fenser function reads with the Bessel function zero order ⇒ ${\rm J}_0(x)$, the parameter $\alpha=3.5$ and the window length $N$: | |
:$$w_\nu = \frac{ {\rm J}_0\big(\pi \cdot \alpha \cdot \sqrt{1 - (2\nu/N)^2}\big)}{ {\rm J}_0\big(\pi \cdot \alpha \big)}.$$ | :$$w_\nu = \frac{ {\rm J}_0\big(\pi \cdot \alpha \cdot \sqrt{1 - (2\nu/N)^2}\big)}{ {\rm J}_0\big(\pi \cdot \alpha \big)}.$$ | ||
Auf der Seite [[Signaldarstellung/Spektralanalyse#G.C3.BCtekriterien_von_Fensterfunktionen|Gütekriterien von Fensterfunktionen]] sind u.a. die Kenngrößen des Kaiser–Bessel–Fensters angegeben: | Auf der Seite [[Signaldarstellung/Spektralanalyse#G.C3.BCtekriterien_von_Fensterfunktionen|Gütekriterien von Fensterfunktionen]] sind u.a. die Kenngrößen des Kaiser–Bessel–Fensters angegeben: | ||
Revision as of 16:57, 21 August 2018
Contents
Applet Description
This applet allows the calculation and graphical representation of the Bessel functions of the first kind and $n$–th order according to the series representation:
- $${\rm J}_n (x) = \sum\limits_{k=0}^{\infty}\frac{(-1)^k \cdot (x/2)^{n \hspace{0.05cm} + \hspace{0.05cm} 2 \hspace{0.02cm}\cdot \hspace{0.05cm}k}}{k! \cdot (n+k)!} \hspace{0.05cm}.$$
- Graphically represented, the functions ${\rm J}_n (x)$ for the order $n=0$ to $n=9$ can become different colors.
- The left-hand output provides the function values ${\rm J}_0 (x = x_1)$, ... , ${\rm J}_9 (x = x_1)$ for a slider-settable value $x_1$ in the range $0 \le x_1 \le 15$ with increment $0.5$.
- The right hand side returns the function values ${\rm J}_0 (x = x_2)$, ... , ${\rm J}_9 (x = x_2)$ for a slider-settable value $x_2$ (same range and value) Increment as on the left).
Theoretical Background
General Information about the Bessel Functions
Bessel functions (or cylinder functions) are solutions of the Bessel differential equation of the form
- $$x^2 \cdot \frac{ {\rm d}^2}{{\rm d}x^2}\ {\rm J}_n (x) \ + \ x \cdot \frac{ {\rm d}}{{\rm d}x}\ {\rm J}_n (x) \ + \ (x^2 - n^2) \cdot {\rm J}_n (x)= 0. $$
This is an ordinary second-order linear differential equation. The parameter $ n $ is usually integer, as in this program. These mathematical functions, which were introduced in 1844 by Friedrich Wilhelm Bessel, can also be represented in closed form as integrals:
- $${\rm J}_n (x) = \frac{1}{2\pi}\cdot \int_{-\pi}^{+\pi} {{\rm e}^{\hspace{0.05cm}{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}[\hspace{0.05cm}x \hspace{0.05cm}\cdot \hspace{0.05cm}\sin(\alpha) -\hspace{0.05cm} n \hspace{0.05cm}\cdot \hspace{0.05cm}\alpha \hspace{0.05cm}]}}\hspace{0.1cm}{\rm d}\alpha \hspace{0.05cm}.$$
The functions ${\rm J}_n (x)$ belong to the class of Bessel functions of the first kind (German: Besselfunktionen erster Art). The parameter $n$ is called the Order.
Annotation: There are a number of modifications of the Bessel functions, including the second-order Bessel functions named ${\rm Y}_n (x)$. For integer $n$, ${\rm Y}_n (x)$ can be replaced by ${\rm J}_n (x)$–functions. However, in this applet, only the first-order Bessel functions are ⇒ ${\rm J}_n (x)$ is considered.
Properties of the Bessel Functions
$\text{Property (A):}$ If the function values for $n = 0$ and $n = 1$ are known, then the Bessel function for $n ≥ 2$ can be determined iteratively:
- $${\rm J}_n (x) ={2 \cdot (n-1)}/{x} \cdot {\rm J}_{n-1} (x) - {\rm J}_{n-2} (x) \hspace{0.05cm}.$$
$\text{Example (A):}$ Consider ${\rm J}_0 (x = 2) = 0.22389$ and ${\rm J}_1 (x= 2) = 0.57672$. From this it can be calculated iteratively:
- $${\rm J}_2 (x= 2) ={2 \cdot 1}/{2} \cdot {\rm J}_{1} (x= 2) - {\rm J}_{0} (x= 2) = 0.57672 - 0.22389 = \hspace{0.15cm}\underline{0.35283}\hspace{0.05cm},$$
- $${\rm J}_3 (x= 2) ={2 \cdot 2}/{2} \cdot {\rm J}_{2} (x= 2) - {\rm J}_{1} (x= 2) = 2 \cdot 0.35283 - 0.57672 = \hspace{0.15cm}\underline{0.12894}\hspace{0.05cm},$$
- $${\rm J}_4 (x= 2) ={2 \cdot 3}/{2} \cdot {\rm J}_{3} (x= 2) - {\rm J}_{2} (x= 2) = 3 \cdot 0.12894 - 0.35283 = \hspace{0.15cm}\underline{0.03400}\hspace{0.05cm}.$$
$\text{Property (B):}$ The symmetry relationship applies ${\rm J}_{–n}(x) = (–1)^n · {\rm J}_n(x)$:
- $${\rm J}_{-1}(x) = - {\rm J}_{1}(x), \hspace{0.3cm}{\rm J}_{-2}(x) = {\rm J}_{2}(x), \hspace{0.3cm}{\rm J}_{-3}(x) = - {\rm J}_{3}(x).$$
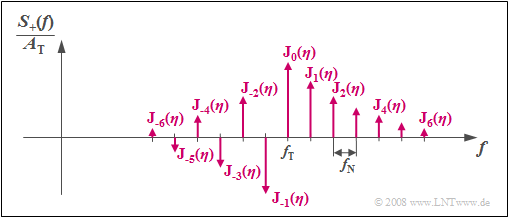
$\text{Example (B):}$ For the spectrum of the analytic signal, in phase modulation of a sinusoidal signal:
- $$S_{\rm +}(f) = A_{\rm T} \cdot \sum_{n = - \infty}^{+\infty}{\rm J}_n (\eta) \cdot \delta \big[f - (f_{\rm T}+ n \cdot f_{\rm N})\big]\hspace{0.05cm}.$$
Denote this
- $f_{\rm T}$ the carrier frequency,
- $f_{\rm N}$ the message frequency,
- $A_{\rm T}$ the carrier amplitude.
The parameter of the Bessel functions in this application is the modulation index $\eta$.
Based on the graphic, the following statements are possible:
- Here $S_+(f)$ consists of an infinite number of discrete lines at a distance of $f_{\rm N}$.
- It is thus in principle infinitely extended.
- The weights of the spectral lines at $f_{\rm T} + n · f_{\rm N}$ ($n$ integer) are determined by the modulation index $η$ over the Bessel functions ${\rm J}_n(η)$.
- The spectral lines are real in the case of a sinusoidal source signal and a cosinusoidal carrier and symmetric about $f_{\rm T}$ for even $n$.
- For odd $n$ , a sign change according to the $\text{Property (B)}$ has to be considered.
- The phase modulation of another phase oscillation of source and / or carrier signal provides the same magnitude spectrum.
Applications of the Bessel Functions
The applications of the Bessel functions in nature–and engineering are diverse and play an important role in physics, for example:
- Examination of natural vibrations of cylindrical resonators,
- Solution of the radial Schrödinger-equation,
- Sound pressure amplitudes of low-viscosity rotational flows,
- Heat conduction in cylindrical bodies,
- Scattering problem of a grid,
- Dynamics of oscillating bodies,
- Angular resolution.
The Bessel functions are counted among the special functions because of their many applications in mathematical physics.
In the following, we restrict ourselves to a few areas that are addressed in our tutorial $\rm LNTwww$.
In the English original Electromagnetic waves in a cylindrical waveguide Pressure amplitudes of inviscid rotational flows Heat conduction in a cylindrical object Modes of vibration of a thin circular (or annular) acoustic membrane (such as a drum or other membranophone) Diffusion problems on a lattice Solutions to the radial Schrödinger equation (in spherical and cylindrical coordinates) for a free particle Solving for patterns of acoustical radiation Frequency-dependent friction in circular pipelines Dynamics of floating bodies Angular resolution The Ende
$\text{Example (C):} \hspace{0.5cm} \text{Use in spectral analysis} \ \Rightarrow \ \text{Kaiser-Bessel filter}$
The spectral leakage effect is the falsification of the spectrum of a periodic and hence temporally unlimited signal due to the implicit time limitation of the discrete Fourier transform (DFT). This will be done, for example, by a spectrum analyzer
- in the time signal not existing frequency components simulated, and / or
- actually existing spectral components are obscured by sidelobes.
The task of the spectral analysis is to limit the influence of the spectral leakage effect by providing suitable window functions.
Such a window function provides, for example, the Kaiser–Bessel–window ⇒ see section Special Window Functions. Its time-discrete Fenser function reads with the Bessel function zero order ⇒ ${\rm J}_0(x)$, the parameter $\alpha=3.5$ and the window length $N$:
- $$w_\nu = \frac{ {\rm J}_0\big(\pi \cdot \alpha \cdot \sqrt{1 - (2\nu/N)^2}\big)}{ {\rm J}_0\big(\pi \cdot \alpha \big)}.$$
Auf der Seite Gütekriterien von Fensterfunktionen sind u.a. die Kenngrößen des Kaiser–Bessel–Fensters angegeben:
- Günstig sind der große „Minimale Abstand zwischen Hauptkeule und Seitenkeulen” und der gewünscht kleine „Maximale Skalierungsfehler”.
- Aufgrund der sehr großen „Äquivalenten Rauschbreite” schneidet das Kaiser–Bessel–Fenster im wichtigsten Vergleichskriterium „Maximaler Prozessverlust” doch schlechter ab als die etablierten Hamming– und Hanning–Fenster.
$\text{Beispiel (D):} \hspace{0.5cm} \text{Rice-Fading-Kanalmodell}$
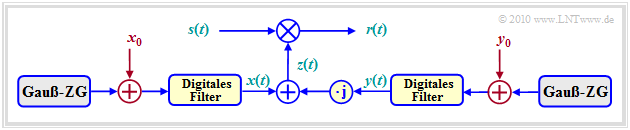
Die Rayleigh–Verteilung beschreibt den Mobilfunkkanal unter der Annahme, dass kein direkter Pfad vorhanden ist und sich somit der multiplikative Faktor $z(t) = x(t) + {\rm j} \cdot y(t)$ allein aus diffus gestreuten Komponenten zusammensetzt.
Bei Vorhandensein einer Direktkomponente (englisch: Line of Sight, LoS) muss man im Modell zu den mittelwertfreien Gaußprozessen $x(t)$ und $y(t)$ noch Gleichkomponenten $x_0$ und/oder $y_0$ hinzufügen:
$$\hspace{0.2cm}x(t) \hspace{0.1cm} \Rightarrow \hspace{0.1cm} x(t) +x_0 \hspace{0.05cm}, \hspace{0.2cm} y(t) \hspace{0.1cm} \Rightarrow \hspace{0.1cm} y(t) +y_0\hspace{0.05cm},$$
$$\hspace{0.2cm}z(t) = x(t) + {\rm j} \cdot y(t) \hspace{0.1cm} \Rightarrow \hspace{0.1cm} z(t) +z_0 \hspace{0.05cm},\hspace{0.2cm} z_0 = x_0 + {\rm j} \cdot y_0\hspace{0.05cm}.$$
Die Grafik zeigt das Rice–Fading–Kanalmodell. Es lässt sich wie folgt zusammenfassen:
- Der Realteil $x(t)$ ist gaußverteilt mit Mittelwert $x_0$ und Varianz $\sigma ^2$.
- Der Imaginärteil $y(t)$ ist ebenfalls gaußverteilt (Mittelwert $y_0$, gleiche Varianz $\sigma ^2$) sowie unabhängig von $x(t)$.
- Für $z_0 \ne 0$ ist der Betrag $\vert z(t)\vert$ riceverteilt, woraus die Bezeichnung „Rice–Fading” herrührt.
- Zur Vereinfachung der Schreibweise setzen wir $\vert z(t)\vert = a(t)$. Für $a < 0$ ist die Betrags–WDF $f_a(a) \equiv 0$, für $a \ge 0$ gilt folgende Gleichung, wobei ${\rm I_0}(x)$ die modifizierte Besselfunktion nullter Ordnung bezeichnet:
- $$f_a(a) = \frac{a}{\sigma^2} \cdot {\rm e}^{ - (a^2 + \vert z_0 \vert ^2)/(2\sigma^2)} \cdot {\rm I}_0 \left [ \frac{a \cdot \vert z_0 \vert}{\sigma^2} \right ] \hspace{0.5cm}\text{mit}\hspace{0.5cm}{\rm I }_0 (u) = {\rm J }_0 ({\rm j} \cdot u) = \sum_{k = 0}^{\infty} \frac{ (u/2)^{2k} }{k! \cdot \Gamma (k+1)} \hspace{0.05cm}.$$
- Zwischen der modifizierten Besselfunktion und der herkömmlichen Besselfunktion ${\rm I_0}(x)$ – jeweils erster Art – besteht also der Zusammenhang ${\rm I }_0 (u) = {\rm J }_0 ({\rm j} \cdot u)$.
$\text{Beispiel (E):} \hspace{0.5cm} \text{Analyse des Frequenzspektrums von frequenzmodulierten Signalen}$
Im $\text{Beispiel (B)}$ wurde bereits gezeigt, dass die Winkelmodulation einer harmonischen Schwingung der Frequenz $f_{\rm N}$ zu einem Linienspektrum führt. Die Spektrallinien liegen um die Trägerfrequenz $f_{\rm T}$ bei $f_{\rm T} + n \cdot f_{\rm N}$ mit $n \in \{ \ \text{...}, -2, -1, \ 0, +1, +2, \text{...} \ \}$. Die Gewichte der Diraclinien sind ${\rm J }_n(\eta)$, abhängig vom Modulationsindex $\eta$.
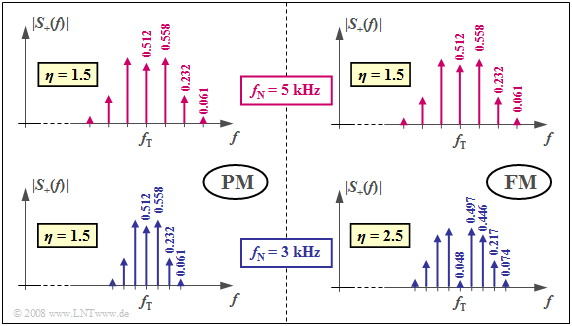
Die Grafik zeigt das Betragsspektrum $\vert S_{\rm +}(f) \vert$ des analytischen Signals bei Phasenmodulation (PM) und Frequenzmodulation (FM), zwei unterschiedliche Formen der Winkelmodulation (WM). Bessellinien mit Werten kleiner als $0.03$ sind hierbei in beiden Fällen vernachlässigt.
Für die obere Bildhälfte sind die Modulatorparameter so gewählt, dass sich für $f_{\rm N} = 5 \ \rm kHz$ jeweils ein Besselspektrum mit dem Modulationsindex $η = 1.5$ ergibt. Lässt man die Phasenbeziehungen außer Acht, so ergeben sich für beide Systeme gleiche Spektren und gleiche Signale.
Die unteren Grafiken gelten bei sonst gleichen Einstellungen für die Nachrichtenfrequenz $f_{\rm N} = 3 \ \rm kHz$. Man erkennt:
- Bei der Phasenmodulation ergibt sich gegenüber $f_{\rm N} = 5 \ \rm kHz$ eine schmalere Spektralfunktion, da nun der Abstand der Bessellinien nur mehr $3 \ \rm kHz$ beträgt. Da bei PM der Modulationsindex unabhängig von $f_{\rm N}$ ist, ergeben sich die gleichen Besselgewichte wie bei $f_{\rm N} = 5 \ \rm kHz$.
- Auch bei der Frequenzmodulation treten nun die Bessellinien im Abstand von $3 \ \rm kHz$ auf. Da aber bei FM der Modulationsindex umgekehrt proportional zu $f_{\rm N}$ ist, gibt es nun unten aufgrund des größeren Modulationsindex $η = 2.5$ deutlich mehr Bessellinien als im rechten oberen (für $η = 1.5$ gültigen) Diagramm.
Das folgende Kapitel muss noch angepasst werden!
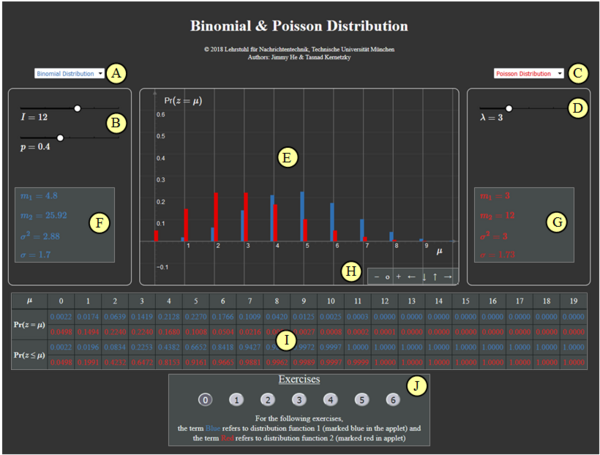
Zur Handhabung des Applets
(A) Vorauswahl für blauen Parametersatz
(B) Parametereingabe $I$ und $p$ per Slider
(C) Vorauswahl für roten Parametersatz
(D) Parametereingabe $\lambda$ per Slider
(E) Graphische Darstellung der Verteilungen
(F) Momentenausgabe für blauen Parametersatz
(G) Momentenausgabe für roten Parametersatz
(H) Variation der grafischen Darstellung
$\hspace{1.5cm}$„$+$” (Vergrößern),
$\hspace{1.5cm}$ „$-$” (Verkleinern)
$\hspace{1.5cm}$ „$\rm o$” (Zurücksetzen)
$\hspace{1.5cm}$ „$\leftarrow$” (Verschieben nach links), usw.
( I ) Ausgabe von ${\rm Pr} (z = \mu)$ und ${\rm Pr} (z \le \mu)$
(J) Bereich für die Versuchsdurchführung
Andere Möglichkeiten zur Variation der grafischen Darstellung:
- Gedrückte Shifttaste und Scrollen: Zoomen im Koordinatensystem,
- Gedrückte Shifttaste und linke Maustaste: Verschieben des Koordinatensystems.
Über die Autoren
Dieses interaktive Berechnungstool wurde am Lehrstuhl für Nachrichtentechnik der Technischen Universität München konzipiert und realisiert.
- Die erste Version wurde 2006 von Markus Elsberger und Slim Lamine im Rahmen von Abschlussarbeiten mit „FlashMX–Actionscript” erstellt (Betreuer: Günter Söder).
- 2018 wurde das Programm von Xiaohan Liu (Bachelorarbeit, Betreuer: Tasnád Kernetzky ) auf „HTML5” umgesetzt.