Difference between revisions of "Applets:Bessel functions of the first kind"
| Line 163: | Line 163: | ||
==Zur Handhabung des Applets== | ==Zur Handhabung des Applets== | ||
| − | [[File: | + | [[File:Bessel_abzug3.png|left|600px]] |
| − | '''(A)''' | + | '''(A)''' Summenformel der Besselfunktionen ${\rm J}_n(x)$ |
| − | '''(B)''' | + | '''(B)''' Auswahl der Ordnung $n$ für die grafische Darstellung |
| − | '''(C)''' | + | '''(C)''' Graphische Darstellung der Besselfunktionen |
| − | '''(D | + | '''(D)''' Variation der grafischen Darstellung |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
$\hspace{1.5cm}$„$+$” (Vergrößern), | $\hspace{1.5cm}$„$+$” (Vergrößern), | ||
| Line 188: | Line 180: | ||
$\hspace{1.5cm}$ „$\leftarrow$” (Verschieben nach links), usw. | $\hspace{1.5cm}$ „$\leftarrow$” (Verschieben nach links), usw. | ||
| − | '''( | + | '''(E)''' Auswahl des Abszissenwertes $x_1$ für die linke Numerikausgabe |
| − | '''(J)''' | + | '''(F)''' Numerikausgabe der Besselfunktionswerte ${\rm J}_n(x_1)$ |
| + | |||
| + | '''(G)''' Auswahl des Abszissenwertes $x_2$ für die rechte Numerikausgabe | ||
| + | |||
| + | '''(F)''' Numerikausgabe der Besselfunktionswerte ${\rm J}_n(x_2)$ | ||
<br clear=all> | <br clear=all> | ||
| − | |||
| − | |||
| − | |||
| − | |||
Revision as of 14:12, 23 August 2018
Contents
Programmbeschreibung
Dieses Applet ermöglicht die Berechnung und graphische Darstellung der Besselfunktionen erster Art und $n$–ter Ordnung entsprechend der Reihendarstellung:
- $${\rm J}_n (x) = \sum\limits_{k=0}^{\infty}\frac{(-1)^k \cdot (x/2)^{n \hspace{0.05cm} + \hspace{0.05cm} 2 \hspace{0.02cm}\cdot \hspace{0.05cm}k}}{k! \cdot (n+k)!} \hspace{0.05cm}.$$
- Graphisch dargestellt können die Funktionen ${\rm J}_n (x)$ für die Ordnung $n=0$ bis $n=9$ in verschiedenen Farben werden.
- Die linke Ausgabe liefert die Funktionswerte ${\rm J}_0 (x = x_1)$, ... , ${\rm J}_9 (x = x_1)$ für einen per Slider einstellbaren Wert $x_1$ im Bereich $0 \le x_1 \le 15$ mit Schrittweite $0.5$.
- Die rechte Ausgabe liefert die Funktionswerte ${\rm J}_0 (x = x_2)$, ... , ${\rm J}_9 (x = x_2)$ für einen per Slider einstellbaren Wert $x_2$ (gleicher Wertebereich und Schrittweite wie links).
Theoretischer Hintergrund
Allgemeines zu den Besselfunktionen
Besselfunktionen (oder auch Zylinderfunktionen) sind Lösungen der Besselschen Differentialgleichung der Form
- $$x^2 \cdot \frac{ {\rm d}^2}{{\rm d}x^2}\ {\rm J}_n (x) \ + \ x \cdot \frac{ {\rm d}}{{\rm d}x}\ {\rm J}_n (x) \ + \ (x^2 - n^2) \cdot {\rm J}_n (x)= 0. $$
Hierbei handelt es sich um eine gewöhnliche lineare Differentialgleichung zweiter Ordnung. Der Parameter $n$ ist meistens ganzzahlig, so auch in diesem Programm. Diese bereits 1844 von Friedrich Wilhelm Bessel eingeführten mathematischen Funktionen können auch in geschlossener Form als Integrale dargestellt werden:
- $${\rm J}_n (x) = \frac{1}{2\pi}\cdot \int_{-\pi}^{+\pi} {{\rm e}^{\hspace{0.05cm}{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}[\hspace{0.05cm}x \hspace{0.05cm}\cdot \hspace{0.05cm}\sin(\alpha) -\hspace{0.05cm} n \hspace{0.05cm}\cdot \hspace{0.05cm}\alpha \hspace{0.05cm}]}}\hspace{0.1cm}{\rm d}\alpha \hspace{0.05cm}.$$
Die Funktionen ${\rm J}_n (x)$ gehören zur Klasse der Besselfunktionen erster Art (englisch: Bessel Functions of the First Kind). Den Parameter $n$ nennt man die Ordnung.
Anmerkung: Es gibt eine Vielzahl von Abwandlungen der Besselfunktionen, unter anderem die mit ${\rm Y}_n (x)$ benannten Besselfunktionen zweiter Art. Für ganzzahliges $n$ lässt sich ${\rm Y}_n (x)$ durch ${\rm J}_n (x)$–Funktionen ausdrücken. In diesem Applet werden jedoch nur die Besselfunktionen erster Art ⇒ ${\rm J}_n (x)$ betrachtet.
Eigenschaften der Besselfunktionen
$\text{Eigenschaft (A):}$ Sind die Funktionswerte für $n = 0$ und $n = 1$ bekannt, so können daraus die Besselfunktionen für $n ≥ 2$ iterativ ermittelt werden:
- $${\rm J}_n (x) ={2 \cdot (n-1)}/{x} \cdot {\rm J}_{n-1} (x) - {\rm J}_{n-2} (x) \hspace{0.05cm}.$$
$\text{Beispiel (A):}$ Es gelte ${\rm J}_0 (x = 2) = 0.22389$ und ${\rm J}_1 (x= 2) = 0.57672$. Daraus können iterativ berechnet werden:
- $${\rm J}_2 (x= 2) ={2 \cdot 1}/{2} \cdot {\rm J}_{1} (x= 2) - {\rm J}_{0} (x= 2) = 0.57672 - 0.22389 = \hspace{0.15cm}\underline{0.35283}\hspace{0.05cm},$$
- $${\rm J}_3 (x= 2) ={2 \cdot 2}/{2} \cdot {\rm J}_{2} (x= 2) - {\rm J}_{1} (x= 2) = 2 \cdot 0.35283 - 0.57672 = \hspace{0.15cm}\underline{0.12894}\hspace{0.05cm},$$
- $${\rm J}_4 (x= 2) ={2 \cdot 3}/{2} \cdot {\rm J}_{3} (x= 2) - {\rm J}_{2} (x= 2) = 3 \cdot 0.12894 - 0.35283 = \hspace{0.15cm}\underline{0.03400}\hspace{0.05cm}.$$
$\text{Eigenschaft (B):}$ Es gilt die Symmetriebeziehung ${\rm J}_{–n}(x) = (–1)^n · {\rm J}_n(x)$:
- $${\rm J}_{-1}(x) = - {\rm J}_{1}(x), \hspace{0.3cm}{\rm J}_{-2}(x) = {\rm J}_{2}(x), \hspace{0.3cm}{\rm J}_{-3}(x) = - {\rm J}_{3}(x).$$
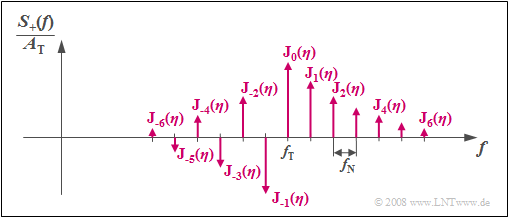
$\text{Beispiel (B):}$ Für das Spektrum des analytischen Signals gilt bei Phasenmodulation eines Sinussignals:
- $$S_{\rm +}(f) = A_{\rm T} \cdot \sum_{n = - \infty}^{+\infty}{\rm J}_n (\eta) \cdot \delta \big[f - (f_{\rm T}+ n \cdot f_{\rm N})\big]\hspace{0.05cm}.$$
Hierbei bezeichnen
- $f_{\rm T}$ die Trägerfrequenz,
- $f_{\rm N}$ die Nachrichtenfrequenz,
- $A_{\rm T}$ die Trägeramplitude.
Der Parameter der Besselfunktionen ist bei dieser Anwendung der Modulationsindex $\eta$.
Anhand der Grafik sind folgende Aussagen möglich:
- $S_+(f)$ besteht hier aus unendlich vielen diskreten Linien im Abstand von $f_{\rm N}$.
- Es ist somit prinzipiell unendlich weit ausgedehnt.
- Die Gewichte der Spektrallinien bei $f_{\rm T} + n · f_{\rm N}$ ($n$ ganzzahlig) sind durch den Modulationsindex $η$ über die Besselfunktionen ${\rm J}_n(η)$ festgelegt.
- Die Spektrallinien sind bei sinusförmigem Quellensignal und cosinusförmigem Träger reell und für gerades $n$ symmetrisch um $f_{\rm T}$.
- Bei ungeradem $n$ ist ein Vorzeichenwechsel entsprechend der $\text{Eigenschaft (B)}$ zu berücksichtigen.
- Die Phasenmodulation einer Schwingung mit anderer Phase von Quellen– und/oder Trägersignal liefert das gleiche Betragsspektrum.
Anwendungen der Besselfunktionen
Die Anwendungen der Besselfunktionen in den Natur– und Ingenieurswissenschaften sind vielfältig und spielen eine wichtige Rolle in der Physik, zum Beispiel:
- Untersuchung von Eigenschwingungen von zylindrischen Resonatoren,
- Lösung der radialen Schrödinger–Gleichung,
- Schalldruckamplituden von dünnflüssgigen Rotationsströmen,
- Wärmeleitung in zylindrischen Körpern,
- Streuungsproblem eines Gitters,
- Dynamik von Schwingkörpern,
- Winkelauflösung.
Man zählt die Besselfunktionen wegen ihrer vielfältigen Anwendungen in der mathematischen Physik zu den speziellen Funktionen.
Wir beschränken uns im Folgenden auf einige Gebiete, die in unserem Lerntutorial $\rm LNTwww$ angesprochen werden.
Im enlischen Original Electromagnetic waves in a cylindrical waveguide Pressure amplitudes of inviscid rotational flows Heat conduction in a cylindrical object Modes of vibration of a thin circular (or annular) acoustic membrane (such as a drum or other membranophone) Diffusion problems on a lattice Solutions to the radial Schrödinger equation (in spherical and cylindrical coordinates) for a free particle Solving for patterns of acoustical radiation Frequency-dependent friction in circular pipelines Dynamics of floating bodies Angular resolution Ende
$\text{Beispiel (C):} \hspace{0.5cm} \text{Einsatz in der Spektralanalyse} \ \Rightarrow \ \text{Kaiser-Bessel-Filter}$
Als spektralen Leckeffekt bezeichnet man die Verfälschung des Spektrums eines periodischen und damit zeitlich unbegrenzten Signals aufgrund der impliziten Zeitbegrenzung der Diskreten Fouriertransformation (DFT). Dadurch werden zum Beispiel von einem Spektrumanalyzer
- im Zeitsignal nicht vorhandene Frequenzanteile vorgetäuscht, und/oder
- tatsächlich vorhandene Spektralkomponenten durch Seitenkeulen verdeckt.
Aufgabe der Spektralanalyse ist es, durch die Bereitstellung geeigneter Fensterfunktionen den Einfluss des spektralen Leckeffektes zu begrenzen.
Eine solche Fensterfunktion liefert zum Beispiel das Kaiser–Bessel–Fenster ⇒ siehe Abschnitt Spezielle Fensterfunktionen. Dessen zeitdiskrete Fenserfunktion lautet mit der Besselfunktion nullter Ordnung ⇒ ${\rm J}_0(x)$, dem Parameter $\alpha=3.5$ und der Fensterlänge $N$:
- $$w_\nu = \frac{ {\rm J}_0\big(\pi \cdot \alpha \cdot \sqrt{1 - (2\nu/N)^2}\big)}{ {\rm J}_0\big(\pi \cdot \alpha \big)}.$$
Auf der Seite Gütekriterien von Fensterfunktionen sind u.a. die Kenngrößen des Kaiser–Bessel–Fensters angegeben:
- Günstig sind der große „Minimale Abstand zwischen Hauptkeule und Seitenkeulen” und der gewünscht kleine „Maximale Skalierungsfehler”.
- Aufgrund der sehr großen „Äquivalenten Rauschbreite” schneidet das Kaiser–Bessel–Fenster im wichtigsten Vergleichskriterium „Maximaler Prozessverlust” doch schlechter ab als die etablierten Hamming– und Hanning–Fenster.
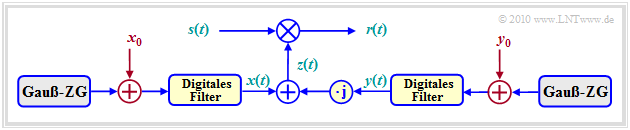
$\text{Beispiel (D):} \hspace{0.5cm} \text{Rice-Fading-Kanalmodell}$
Die Rayleigh–Verteilung beschreibt den Mobilfunkkanal unter der Annahme, dass kein direkter Pfad vorhanden ist und sich somit der multiplikative Faktor $z(t) = x(t) + {\rm j} \cdot y(t)$ allein aus diffus gestreuten Komponenten zusammensetzt.
Bei Vorhandensein einer Direktkomponente (englisch: Line of Sight, LoS) muss man im Modell zu den mittelwertfreien Gaußprozessen $x(t)$ und $y(t)$ noch Gleichkomponenten $x_0$ und/oder $y_0$ hinzufügen:
$$\hspace{0.2cm}x(t) \hspace{0.1cm} \Rightarrow \hspace{0.1cm} x(t) +x_0 \hspace{0.05cm}, \hspace{0.2cm} y(t) \hspace{0.1cm} \Rightarrow \hspace{0.1cm} y(t) +y_0\hspace{0.05cm},$$
$$\hspace{0.2cm}z(t) = x(t) + {\rm j} \cdot y(t) \hspace{0.1cm} \Rightarrow \hspace{0.1cm} z(t) +z_0 \hspace{0.05cm},\hspace{0.2cm} z_0 = x_0 + {\rm j} \cdot y_0\hspace{0.05cm}.$$
Die Grafik zeigt das Rice–Fading–Kanalmodell. Es lässt sich wie folgt zusammenfassen:
- Der Realteil $x(t)$ ist gaußverteilt mit Mittelwert $x_0$ und Varianz $\sigma ^2$.
- Der Imaginärteil $y(t)$ ist ebenfalls gaußverteilt (Mittelwert $y_0$, gleiche Varianz $\sigma ^2$) sowie unabhängig von $x(t)$.
- Für $z_0 \ne 0$ ist der Betrag $\vert z(t)\vert$ riceverteilt, woraus die Bezeichnung „Rice–Fading” herrührt.
- Zur Vereinfachung der Schreibweise setzen wir $\vert z(t)\vert = a(t)$. Für $a < 0$ ist die Betrags–WDF $f_a(a) \equiv 0$, für $a \ge 0$ gilt folgende Gleichung, wobei ${\rm I_0}(x)$ die modifizierte Besselfunktion nullter Ordnung bezeichnet:
- $$f_a(a) = \frac{a}{\sigma^2} \cdot {\rm e}^{ - (a^2 + \vert z_0 \vert ^2)/(2\sigma^2)} \cdot {\rm I}_0 \left [ \frac{a \cdot \vert z_0 \vert}{\sigma^2} \right ] \hspace{0.5cm}\text{mit}\hspace{0.5cm}{\rm I }_0 (u) = {\rm J }_0 ({\rm j} \cdot u) = \sum_{k = 0}^{\infty} \frac{ (u/2)^{2k} }{k! \cdot \Gamma (k+1)} \hspace{0.05cm}.$$
- Zwischen der modifizierten Besselfunktion und der herkömmlichen Besselfunktion ${\rm I_0}(x)$ – jeweils erster Art – besteht also der Zusammenhang ${\rm I }_0 (u) = {\rm J }_0 ({\rm j} \cdot u)$.
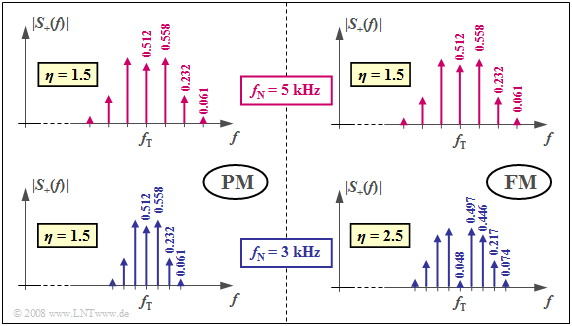
$\text{Beispiel (E):} \hspace{0.5cm} \text{Analyse des Frequenzspektrums von frequenzmodulierten Signalen}$
Im $\text{Beispiel (B)}$ wurde bereits gezeigt, dass die Winkelmodulation einer harmonischen Schwingung der Frequenz $f_{\rm N}$ zu einem Linienspektrum führt. Die Spektrallinien liegen um die Trägerfrequenz $f_{\rm T}$ bei $f_{\rm T} + n \cdot f_{\rm N}$ mit $n \in \{ \ \text{...}, -2, -1, \ 0, +1, +2, \text{...} \ \}$. Die Gewichte der Diraclinien sind ${\rm J }_n(\eta)$, abhängig vom Modulationsindex $\eta$.
Die Grafik zeigt das Betragsspektrum $\vert S_{\rm +}(f) \vert$ des analytischen Signals bei Phasenmodulation (PM) und Frequenzmodulation (FM), zwei unterschiedliche Formen der Winkelmodulation (WM). Bessellinien mit Werten kleiner als $0.03$ sind hierbei in beiden Fällen vernachlässigt.
Für die obere Bildhälfte sind die Modulatorparameter so gewählt, dass sich für $f_{\rm N} = 5 \ \rm kHz$ jeweils ein Besselspektrum mit dem Modulationsindex $η = 1.5$ ergibt. Lässt man die Phasenbeziehungen außer Acht, so ergeben sich für beide Systeme gleiche Spektren und gleiche Signale.
Die unteren Grafiken gelten bei sonst gleichen Einstellungen für die Nachrichtenfrequenz $f_{\rm N} = 3 \ \rm kHz$. Man erkennt:
- Bei der Phasenmodulation ergibt sich gegenüber $f_{\rm N} = 5 \ \rm kHz$ eine schmalere Spektralfunktion, da nun der Abstand der Bessellinien nur mehr $3 \ \rm kHz$ beträgt. Da bei PM der Modulationsindex unabhängig von $f_{\rm N}$ ist, ergeben sich die gleichen Besselgewichte wie bei $f_{\rm N} = 5 \ \rm kHz$.
- Auch bei der Frequenzmodulation treten nun die Bessellinien im Abstand von $3 \ \rm kHz$ auf. Da aber bei FM der Modulationsindex umgekehrt proportional zu $f_{\rm N}$ ist, gibt es nun unten aufgrund des größeren Modulationsindex $η = 2.5$ deutlich mehr Bessellinien als im rechten oberen (für $η = 1.5$ gültigen) Diagramm.
Das folgende Kapitel muss noch angepasst werden!
Zur Handhabung des Applets
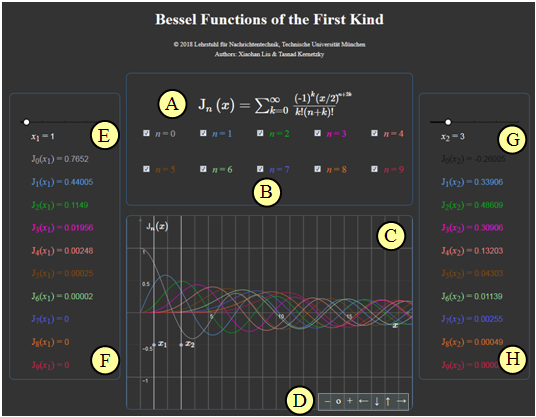
(A) Summenformel der Besselfunktionen ${\rm J}_n(x)$
(B) Auswahl der Ordnung $n$ für die grafische Darstellung
(C) Graphische Darstellung der Besselfunktionen
(D) Variation der grafischen Darstellung
$\hspace{1.5cm}$„$+$” (Vergrößern),
$\hspace{1.5cm}$ „$-$” (Verkleinern)
$\hspace{1.5cm}$ „$\rm o$” (Zurücksetzen)
$\hspace{1.5cm}$ „$\leftarrow$” (Verschieben nach links), usw.
(E) Auswahl des Abszissenwertes $x_1$ für die linke Numerikausgabe
(F) Numerikausgabe der Besselfunktionswerte ${\rm J}_n(x_1)$
(G) Auswahl des Abszissenwertes $x_2$ für die rechte Numerikausgabe
(F) Numerikausgabe der Besselfunktionswerte ${\rm J}_n(x_2)$
Über die Autoren
Dieses interaktive Berechnungstool wurde am Lehrstuhl für Nachrichtentechnik der Technischen Universität München konzipiert und realisiert.
- Die erste Version wurde 2006 von Markus Elsberger und Slim Lamine im Rahmen von Abschlussarbeiten mit „FlashMX–Actionscript” erstellt (Betreuer: Günter Söder).
- 2018 wurde das Programm von Xiaohan Liu (Bachelorarbeit, Betreuer: Tasnád Kernetzky ) auf „HTML5” umgesetzt.