Difference between revisions of "Aufgaben:Exercise 1.5: Binary Markov Source"
m (Textersetzung - „*Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.“ durch „ “) |
|||
| Line 3: | Line 3: | ||
}} | }} | ||
| − | [[File:P_ID2250__Inf_A_1_5.png|right| | + | [[File:P_ID2250__Inf_A_1_5.png|right|frame|Binäres Markovdiagramm]] |
| − | Die [[Aufgaben:1.4_Entropienäherungen_für_den_AMI-Code|Aufgabe 1.4]] hat gezeigt, dass die Berechnung der Entropie bei einer gedächtnisbehafteten Quelle sehr aufwändig sein kann. Man muss dann zunächst (sehr viele) Entropienäherungen $H_k$ für $k$–Tupel berechnen und kann erst dann mit dem Grenzübergang $k \to \infty$ | + | Die [[Aufgaben:1.4_Entropienäherungen_für_den_AMI-Code|Aufgabe 1.4]] hat gezeigt, dass die Berechnung der Entropie bei einer gedächtnisbehafteten Quelle sehr aufwändig sein kann. Man muss dann zunächst (sehr viele) Entropienäherungen $H_k$ für $k$–Tupel berechnen und kann erst dann die Quellenentropie mit dem Grenzübergang $k \to \infty$ ermitteln: |
:$$H = \lim_{k \rightarrow \infty } H_k \hspace{0.05cm}.$$ | :$$H = \lim_{k \rightarrow \infty } H_k \hspace{0.05cm}.$$ | ||
Oft tendiert dabei $H_k$ nur sehr langsam gegen den Grenzwert $H$. | Oft tendiert dabei $H_k$ nur sehr langsam gegen den Grenzwert $H$. | ||
Der Rechengang wird drastisch reduziert, wenn die Nachrichtenquelle Markoveigenschaften besitzt. Die Grafik zeigt das Übergangsdiagramm für eine binäre Markovquelle mit den zwei Zuständen (Symbolen) $\rm A$ und $\rm B$. | Der Rechengang wird drastisch reduziert, wenn die Nachrichtenquelle Markoveigenschaften besitzt. Die Grafik zeigt das Übergangsdiagramm für eine binäre Markovquelle mit den zwei Zuständen (Symbolen) $\rm A$ und $\rm B$. | ||
| − | *Dieses ist durch die beiden bedingten Wahrscheinlichkeiten $p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}B} = p$ und $p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}A} = q$ eindeutig bestimmt. | + | *Dieses ist durch die beiden bedingten Wahrscheinlichkeiten $p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}B} = p$ und $p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}A} = q$ eindeutig bestimmt. |
| − | *Die bedingten Wahrscheinlichkeiten $p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}A}$ und $p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}B}$ sowie die Symbolwahrscheinlichkeiten $p_{\rm A}$ und $p_{\rm B}$ lassen sich daraus ermitteln. | + | *Die bedingten Wahrscheinlichkeiten $p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}A}$ und $p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}B}$ sowie die Symbolwahrscheinlichkeiten $p_{\rm A}$ und $p_{\rm B}$ lassen sich daraus ermitteln. |
| Line 17: | Line 17: | ||
{\rm log}_2\hspace{0.1cm}\frac {1}{ p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}B}} | {\rm log}_2\hspace{0.1cm}\frac {1}{ p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}B}} | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | Bei dieser Gleichung ist zu beachten, dass im Argument des <i>Logarithmus dualis</i> jeweils die [[Stochastische_Signaltheorie/Statistische_Abhängigkeit_und_Unabhängigkeit#Bedingte_Wahrscheinlichkeit|bedingten Wahrscheinlichkeiten]] $p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}A}$, $p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}A}$, ... einzusetzen sind, während für die Gewichtung die [[Stochastische_Signaltheorie/Mengentheoretische_Grundlagen#Schnittmenge|Verbundwahrscheinlichkeiten]] $p_{\rm AA}$, $p_{\rm AB}$, ... zu verwenden sind. | + | Bei dieser Gleichung ist zu beachten, dass im Argument des <i>Logarithmus dualis</i> jeweils die [[Stochastische_Signaltheorie/Statistische_Abhängigkeit_und_Unabhängigkeit#Bedingte_Wahrscheinlichkeit|bedingten Wahrscheinlichkeiten]] $p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}A}$, $p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}A}$, ... einzusetzen sind, während für die Gewichtung die [[Stochastische_Signaltheorie/Mengentheoretische_Grundlagen#Schnittmenge|Verbundwahrscheinlichkeiten]] $p_{\rm AA}$, $p_{\rm AB}$, ... zu verwenden sind. |
Mit der Entropienäherung erster Ordnung, | Mit der Entropienäherung erster Ordnung, | ||
| Line 23: | Line 23: | ||
{\rm log}_2\hspace{0.1cm}\frac {1}{ p_{\rm B}} | {\rm log}_2\hspace{0.1cm}\frac {1}{ p_{\rm B}} | ||
\hspace{0.5cm}({\rm Einheit\hspace{-0.1cm}: \hspace{0.1cm}bit/Symbol})\hspace{0.05cm},$$ | \hspace{0.5cm}({\rm Einheit\hspace{-0.1cm}: \hspace{0.1cm}bit/Symbol})\hspace{0.05cm},$$ | ||
| − | sowie der oben angegebenen (tatsächlichen) Entropie $H = H_{\rm M}$ lassen sich bei einer Markovquelle auch alle weiteren Entropienäherungen ( | + | sowie der oben angegebenen (tatsächlichen) Entropie $H = H_{\rm M}$ lassen sich bei einer Markovquelle auch alle weiteren Entropienäherungen $(k = 2,, 3, \text{...})$ direkt berechnen: |
| − | :$$H_k = \frac{1}{k} \cdot [ H_{\rm 1} + (k-1) \cdot H_{\rm M}] | + | :$$H_k = \frac{1}{k} \cdot \big [ H_{\rm 1} + (k-1) \cdot H_{\rm M} \big ] |
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| + | |||
| + | |||
| + | |||
| Line 31: | Line 34: | ||
*Die Aufgabe gehört zum Kapitel [[Informationstheorie/Nachrichtenquellen_mit_Gedächtnis|Nachrichtenquellen mit Gedächtnis]]. | *Die Aufgabe gehört zum Kapitel [[Informationstheorie/Nachrichtenquellen_mit_Gedächtnis|Nachrichtenquellen mit Gedächtnis]]. | ||
*Bezug genommen wird insbesondere auch auf die beiden Seiten [[Stochastische_Signaltheorie/Mengentheoretische_Grundlagen#Schnittmenge|Schnittmenge]] und [[Stochastische_Signaltheorie/Statistische_Abhängigkeit_und_Unabhängigkeit#Bedingte_Wahrscheinlichkeit|Bedingte Wahrscheinlichkeit]]. | *Bezug genommen wird insbesondere auch auf die beiden Seiten [[Stochastische_Signaltheorie/Mengentheoretische_Grundlagen#Schnittmenge|Schnittmenge]] und [[Stochastische_Signaltheorie/Statistische_Abhängigkeit_und_Unabhängigkeit#Bedingte_Wahrscheinlichkeit|Bedingte Wahrscheinlichkeit]]. | ||
| − | *Mit Ausnahme der Teilaufgabe (6) gelte stets $p = 1/4$ und $q = 1/2$. | + | *Mit Ausnahme der Teilaufgabe '''(6)''' gelte stets $p = 1/4$ und $q = 1/2$. |
*Für die (ergodischen) Symbolwahrscheinlichkeiten einer Markovkette erster Ordnung gilt: | *Für die (ergodischen) Symbolwahrscheinlichkeiten einer Markovkette erster Ordnung gilt: | ||
| Line 38: | Line 41: | ||
p_{\rm B} = \frac {p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}A}} | p_{\rm B} = \frac {p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}A}} | ||
{ p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}B} + p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}A}} \hspace{0.05cm}.$$ | { p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}B} + p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}A}} \hspace{0.05cm}.$$ | ||
| + | |||
| + | |||
| Line 43: | Line 48: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {Geben Sie die Übergangswahrscheinlichkeiten für $p = 1/4$ und $q = 1/2$ an. | + | {Geben Sie die Übergangswahrscheinlichkeiten für $p = 1/4$ und $q = 1/2$ an. |
|type="{}"} | |type="{}"} | ||
| − | $p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}A} \ = $ { 0.5 3% } | + | $p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}A} \ = \ $ { 0.5 3% } |
| − | $p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}B} \ = $ { 0.75 3% } | + | $p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}B} \ = \ $ { 0.75 3% } |
| − | {Wie groß sind die Symbolwahrscheinlichkeiten? Es gelte weiterhin $p = 1/4$ und $q = 1/2$. | + | {Wie groß sind die Symbolwahrscheinlichkeiten? Es gelte weiterhin $p = 1/4$ und $q = 1/2$. |
|type="{}"} | |type="{}"} | ||
| − | $p_{\rm A} \ = $ { 0.333 3% } | + | $p_{\rm A} \ = \ $ { 0.333 3% } |
| − | $p_{\rm B} \ = ${ 0.667 3% } | + | $p_{\rm B} \ = \ ${ 0.667 3% } |
{Geben Sie die dazugehörige Entropienäherung erster Ordnung an. | {Geben Sie die dazugehörige Entropienäherung erster Ordnung an. | ||
|type="{}"} | |type="{}"} | ||
| − | $H_1 \ = $ { 0.918 1% } $\ \rm bit/Symbol$ | + | $H_1 \ = \ $ { 0.918 1% } $\ \rm bit/Symbol$ |
| − | {Welche Entropie $H = H_{\rm M}$ besitzt diese Markovquelle mit $p = 1/4$ und $q = 1/2$? | + | {Welche Entropie $H = H_{\rm M}$ besitzt diese Markovquelle mit $p = 1/4$ und $q = 1/2$? |
|type="{}"} | |type="{}"} | ||
| − | $H \ =$ { 0.875 1% } $\ \rm bit/Symbol$ | + | $H \ = \ $ { 0.875 1% } $\ \rm bit/Symbol$ |
{Welche Näherungen $H_k$ ergeben sich aufgrund der Markoveigenschaften? | {Welche Näherungen $H_k$ ergeben sich aufgrund der Markoveigenschaften? | ||
|type="{}"} | |type="{}"} | ||
| − | $H_2 \ =$ { 0.897 0.5% } $\ \rm bit/Symbol$ | + | $H_2 \ = \ $ { 0.897 0.5% } $\ \rm bit/Symbol$ |
| − | $H_3 \ =$ { 0.889 0.5% } $\ \rm bit/Symbol$ | + | $H_3 \ = \ $ { 0.889 0.5% } $\ \rm bit/Symbol$ |
| − | $H_4 \ =$ { 0.886 0.5% } $\ \rm bit/Symbol$ | + | $H_4 \ = \ $ { 0.886 0.5% } $\ \rm bit/Symbol$ |
| − | {Welche Entropie $H = H_{\rm M}$ besitzt die Markovquelle mit $p = 1/4$ und $q = 3/4$? | + | {Welche Entropie $H = H_{\rm M}$ besitzt die Markovquelle mit $p = 1/4$ und $q = 3/4$? |
|type="{}"} | |type="{}"} | ||
| − | $H \ =$ { 0.811 1% } $\ \rm bit/Symbol$ | + | $H \ = \ $ { 0.811 1% } $\ \rm bit/Symbol$ |
Revision as of 08:29, 19 September 2018
Die Aufgabe 1.4 hat gezeigt, dass die Berechnung der Entropie bei einer gedächtnisbehafteten Quelle sehr aufwändig sein kann. Man muss dann zunächst (sehr viele) Entropienäherungen $H_k$ für $k$–Tupel berechnen und kann erst dann die Quellenentropie mit dem Grenzübergang $k \to \infty$ ermitteln:
- $$H = \lim_{k \rightarrow \infty } H_k \hspace{0.05cm}.$$
Oft tendiert dabei $H_k$ nur sehr langsam gegen den Grenzwert $H$.
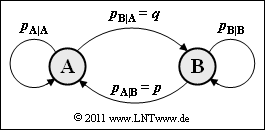
Der Rechengang wird drastisch reduziert, wenn die Nachrichtenquelle Markoveigenschaften besitzt. Die Grafik zeigt das Übergangsdiagramm für eine binäre Markovquelle mit den zwei Zuständen (Symbolen) $\rm A$ und $\rm B$.
- Dieses ist durch die beiden bedingten Wahrscheinlichkeiten $p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}B} = p$ und $p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}A} = q$ eindeutig bestimmt.
- Die bedingten Wahrscheinlichkeiten $p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}A}$ und $p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}B}$ sowie die Symbolwahrscheinlichkeiten $p_{\rm A}$ und $p_{\rm B}$ lassen sich daraus ermitteln.
Die Entropie der binären Markovkette (mit der Einheit „bit/Symbol”) lautet dann:
- $$H = H_{\rm M} = p_{\rm AA} \cdot {\rm log}_2\hspace{0.1cm}\frac {1}{ p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}A}} + p_{\rm AB} \cdot {\rm log}_2\hspace{0.1cm}\frac {1}{ p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}A}} + p_{\rm BA} \cdot {\rm log}_2\hspace{0.1cm}\frac {1}{ p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}B}} + p_{\rm BB} \cdot {\rm log}_2\hspace{0.1cm}\frac {1}{ p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}B}} \hspace{0.05cm}.$$
Bei dieser Gleichung ist zu beachten, dass im Argument des Logarithmus dualis jeweils die bedingten Wahrscheinlichkeiten $p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}A}$, $p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}A}$, ... einzusetzen sind, während für die Gewichtung die Verbundwahrscheinlichkeiten $p_{\rm AA}$, $p_{\rm AB}$, ... zu verwenden sind.
Mit der Entropienäherung erster Ordnung,
- $$H_1 = p_{\rm A} \cdot {\rm log}_2\hspace{0.1cm}\frac {1}{ p_{\rm A}} + p_{\rm B} \cdot {\rm log}_2\hspace{0.1cm}\frac {1}{ p_{\rm B}} \hspace{0.5cm}({\rm Einheit\hspace{-0.1cm}: \hspace{0.1cm}bit/Symbol})\hspace{0.05cm},$$
sowie der oben angegebenen (tatsächlichen) Entropie $H = H_{\rm M}$ lassen sich bei einer Markovquelle auch alle weiteren Entropienäherungen $(k = 2,, 3, \text{...})$ direkt berechnen:
- $$H_k = \frac{1}{k} \cdot \big [ H_{\rm 1} + (k-1) \cdot H_{\rm M} \big ] \hspace{0.05cm}.$$
Hinweise:
- Die Aufgabe gehört zum Kapitel Nachrichtenquellen mit Gedächtnis.
- Bezug genommen wird insbesondere auch auf die beiden Seiten Schnittmenge und Bedingte Wahrscheinlichkeit.
- Mit Ausnahme der Teilaufgabe (6) gelte stets $p = 1/4$ und $q = 1/2$.
- Für die (ergodischen) Symbolwahrscheinlichkeiten einer Markovkette erster Ordnung gilt:
- $$ p_{\rm A} = \frac {p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}B}} { p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}B} + p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}A}} \hspace{0.05cm}, \hspace{0.3cm} p_{\rm B} = \frac {p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}A}} { p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}B} + p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}A}} \hspace{0.05cm}.$$
Fragebogen
Musterlösung
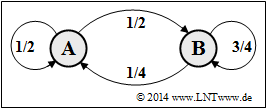
Nach $\rm A$ sind $\rm A$ und $\rm B$ gleichwahrscheinlich. Nach $\rm B$ tritt $\rm B$ sehr viel häufiger als $\rm A$ auf. Für die Übergangswahrscheinlichkeiten gilt:
- $$p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}A} \hspace{0.1cm} = \hspace{0.1cm} 1 - p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}A}= 1 - q \hspace{0.15cm} \underline {= 0.5} \hspace{0.05cm},$$
- $$ p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}B} \hspace{0.1cm} = \hspace{0.1cm} 1 - p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}B}= 1 - p \hspace{0.15cm} \underline {= 0.75} \hspace{0.05cm}.$$
(2) Entsprechend den angegebenen Gleichungen gilt:
- $$p_{\rm A}= \frac{p}{p+q} = \frac{0.25}{0.25 + 0.50} \hspace{0.15cm} \underline {= 0.333} \hspace{0.05cm}, \hspace{0.5cm} p_{\rm B} = \frac{q}{p+q} = \frac{0.50}{0.25 + 0.50} \hspace{0.15cm} \underline {= 0.667} \hspace{0.05cm}.$$
(3) Mit den in der letzten Teilaufgabe berechneten Wahrscheinlichkeiten gilt:
- $$H_{\rm 1} = H_{\rm bin}(p_{\rm A}) = 1/3 \cdot {\rm log}_2\hspace{0.01cm} (3) + 2/3 \cdot {\rm log}_2\hspace{0.01cm} (1.5) = 1.585 - 2/3\hspace{0.15cm} \underline {= 0.918 \,{\rm bit/Symbol}} \hspace{0.05cm}.$$
(4) Die Entropie der Markovquelle lautet entsprechend der Angabe
- $$H = p_{\rm AA} \cdot {\rm log}_2\hspace{0.1cm}\frac {1}{ p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}A}} + p_{\rm AB} \cdot {\rm log}_2\hspace{0.1cm}\frac {1}{ p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}A}} + p_{\rm BA} \cdot {\rm log}_2\hspace{0.1cm}\frac {1}{ p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}B}} + p_{\rm BB} \cdot {\rm log}_2\hspace{0.1cm}\frac {1}{ p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}B}} \hspace{0.05cm}.$$
Für die Verbundwahrscheinlichkeiten gilt:
- $$p_{\rm AA} = p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}A} \cdot p_{\rm A} = (1-q) \cdot \frac{p}{p+q} = \frac{1/2 \cdot 1/4}{3/4} = {1}/{6} \hspace{0.05cm},$$
- $$ p_{\rm AB} = p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}A} \cdot p_{\rm A} = q \cdot \frac{p}{p+q} = \frac{1/2 \cdot 1/4}{3/4} = {1}/{6} \hspace{0.05cm},$$
- $$ p_{\rm BA} = p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}B} \cdot p_{\rm B} = p \cdot \frac{q}{p+q} = p_{\rm AB} = {1}/{6} \hspace{0.05cm},$$
- $$ p_{\rm BB} = p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}B} \cdot p_{\rm B} = (1-p) \cdot \frac{q}{p+q} = \frac{3/4 \cdot 1/2}{3/4} = {1}/{2} $$
- $$\Rightarrow\hspace{0.3cm} H = 1/6 \cdot {\rm log}_2\hspace{0.01cm} (2) + 1/6 \cdot {\rm log}_2\hspace{0.01cm} (2) + 1/6 \cdot {\rm log}_2\hspace{0.01cm} (4) + 1/2 \cdot {\rm log}_2\hspace{0.1cm} (4/3) = 10/6 - 1/2 \cdot {\rm log}_2\hspace{0.01cm} (3) \hspace{0.15cm} \underline {= 0.875 \,{\rm bit/Symbol}} \hspace{0.05cm}.$$
(5) Allgemein gilt mit $H_{\rm M} = H$ für die $k$–Entropienäherung: $H_k = {1}/{k} \cdot [ H_{\rm 1} + (k-1) \cdot H_{\rm M}] \hspace{0.05cm}.$ Daraus folgt:
- $$H_2 = {1}/{2} \cdot [ 0.918 + 1 \cdot 0.875] \hspace{0.15cm} \underline {= 0.897 \,{\rm bit/Symbol}} \hspace{0.05cm},$$
- $$ H_3 = {1}/{3} \cdot [ 0.918 + 2 \cdot 0.875] \hspace{0.15cm} \underline {= 0.889 \,{\rm bit/Symbol}} \hspace{0.05cm},$$
- $$ H_4 = {1}/{4} \cdot [ 0.918 + 3 \cdot 0.875] \hspace{0.15cm} \underline {= 0.886 \,{\rm bit/Symbol}} \hspace{0.05cm}.$$
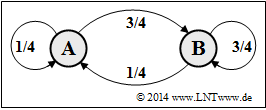
(6) Mit dem neuen Parametersatz ($p = 1/4, q = 3/4$) erhält man für die Symbolwahrscheinlichkeiten: $ p_{\rm A} = 1/4$ und $ p_{\rm B} = 3/4$. Dieser Sonderfall führt demnach zu statistisch unabhängigen Symbolen:
- $$ p_{\rm A} = p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}A} = p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}B} \hspace{0.05cm}, \hspace{0.2cm} p_{\rm B} = p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}A} = p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}B} \hspace{0.05cm}.$$
Damit ist die Entropie $H$ identisch mit der Entropienäherung $H_1$:
- $$H = H_{\rm 1} = 1/4 \cdot {\rm log}_2\hspace{0.01cm} (4) + 3/4 \cdot {\rm log}_2\hspace{0.01cm} (4/3) = 2 - 0.75 \cdot {\rm log}_2\hspace{0.01cm} (3) \hspace{0.15cm} \underline {= 0.811 \,{\rm bit/Symbol}} \hspace{0.05cm}.$$
Die Entropienäherungen $H_2$, $H_3$, $H_4$, ... liefern hier ebenfalls das Ergebnis $0.811 \, \rm bit/Symbol$.