Difference between revisions of "Aufgaben:Exercise 1.2: Distortions? Or no Distortion?"
m (Textersetzung - „*Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.“ durch „ “) |
|||
| Line 3: | Line 3: | ||
}} | }} | ||
| − | [[File:P_ID949__Mod_A_1_2.png|right|frame|Betrachtete Sinkensignale für das gegebene Eingangssignal | + | [[File:P_ID949__Mod_A_1_2.png|right|frame|Betrachtete Sinkensignale für das gegebene Eingangssignal $q(t)$)]] |
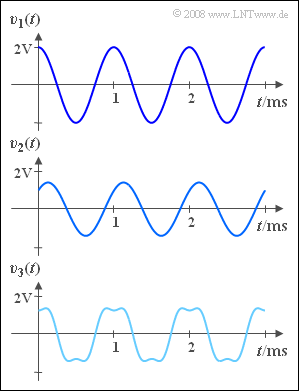
| − | Die | + | Die Nachrichtensysteme $S_1$, $S_2$ und $S_3$ werden hinsichtlich der durch sie verursachten Verzerrungen analysiert. Zu diesem Zwecke wird an den Eingang eines jeden Systems das cosinusförmige Testsignal mit der Signalfrequenz $f_{\rm N} = 1\text{ kHz}$ angelegt: |
:$$q(t) = 2 \;{\rm V} \cdot \cos(2 \pi f_{\rm N} t )$$ | :$$q(t) = 2 \;{\rm V} \cdot \cos(2 \pi f_{\rm N} t )$$ | ||
| − | Gemessen werden die Signale am | + | Gemessen werden die drei Signale am Systemausgang, die in der Grafik dargestellt sind: |
:$$v_1(t) = 2 \;{\rm V} \cdot \cos(2 \pi f_{\rm N} t )\hspace{0.05cm},$$ | :$$v_1(t) = 2 \;{\rm V} \cdot \cos(2 \pi f_{\rm N} t )\hspace{0.05cm},$$ | ||
:$$v_2(t) = 1 \;{\rm V} \cdot \cos(2 \pi f_{\rm N} t + 1 \;{\rm V} \cdot \sin(2 \pi f_{\rm N} t) \hspace{0.05cm},$$ | :$$v_2(t) = 1 \;{\rm V} \cdot \cos(2 \pi f_{\rm N} t + 1 \;{\rm V} \cdot \sin(2 \pi f_{\rm N} t) \hspace{0.05cm},$$ | ||
| Line 13: | Line 13: | ||
Anzumerken ist, dass hier die in der Praxis stets vorhandenen Rauschanteile als vernachlässigbar klein angenommen werden. | Anzumerken ist, dass hier die in der Praxis stets vorhandenen Rauschanteile als vernachlässigbar klein angenommen werden. | ||
| + | |||
| + | |||
| + | |||
''Hinweise:'' | ''Hinweise:'' | ||
| − | *Die Aufgabe gehört zum Kapitel [[Modulationsverfahren/Qualitätskriterien|Qualitätskriterien]]. | + | *Die Aufgabe gehört zum Kapitel [[Modulationsverfahren/Qualitätskriterien|Qualitätskriterien]]. |
| − | *Bezug genommen wird insbesondere auf die Seite [[Modulationsverfahren/Qualitätskriterien#Signal.E2.80.93zu.E2.80.93St.C3.B6r.E2.80.93Leistungsverh.C3.A4ltnis|Signal-zu-Stör-Leistungsverhältnis]] und auf das Kapitel [[Lineare_zeitinvariante_Systeme/Nichtlineare_Verzerrungen|Nichtlineare Verzerrungen]] im Buch „Lineare zeitinvariante Systeme”. | + | *Bezug genommen wird insbesondere auf die Seite [[Modulationsverfahren/Qualitätskriterien#Signal.E2.80.93zu.E2.80.93St.C3.B6r.E2.80.93Leistungsverh.C3.A4ltnis|Signal-zu-Stör-Leistungsverhältnis]] und auf das Kapitel [[Lineare_zeitinvariante_Systeme/Nichtlineare_Verzerrungen|Nichtlineare Verzerrungen]] im Buch „Lineare zeitinvariante Systeme”. |
| − | *Bei nichtlinearen Verzerrungen ist das Sinken–SNR $ρ_v = 1/K^2,$ wobei der Klirrfaktor $K$ das Verhältnis der Effektivwerte aller Oberwellen zum Effektivwert der Grundfrequenz angibt. | + | *Bei nichtlinearen Verzerrungen ist das Sinken–SNR $ρ_v = 1/K^2,$ wobei der Klirrfaktor $K$ das Verhältnis der Effektivwerte aller Oberwellen zum Effektivwert der Grundfrequenz angibt. |
| Line 25: | Line 28: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {Welche Aussagen sind nach dieser Messung über das System $S_1$ möglich? | + | {Welche Aussagen sind nach dieser Messung über das System $S_1$ möglich? |
|type="[]"} | |type="[]"} | ||
| − | - $S_1$ könnte ein ideales System sein. | + | - $S_1$ könnte ein ideales System sein. |
| − | + $S_1$ könnte ein verzerrungsfreies System sein. | + | + $S_1$ könnte ein verzerrungsfreies System sein. |
| − | + $S_1$ könnte ein linear verzerrendes System sein. | + | + $S_1$ könnte ein linear verzerrendes System sein. |
| − | - $S_1$ könnte ein nichtlinear verzerrendes System sein. | + | - $S_1$ könnte ein nichtlinear verzerrendes System sein. |
Revision as of 12:11, 3 December 2018
Die Nachrichtensysteme $S_1$, $S_2$ und $S_3$ werden hinsichtlich der durch sie verursachten Verzerrungen analysiert. Zu diesem Zwecke wird an den Eingang eines jeden Systems das cosinusförmige Testsignal mit der Signalfrequenz $f_{\rm N} = 1\text{ kHz}$ angelegt:
- $$q(t) = 2 \;{\rm V} \cdot \cos(2 \pi f_{\rm N} t )$$
Gemessen werden die drei Signale am Systemausgang, die in der Grafik dargestellt sind:
- $$v_1(t) = 2 \;{\rm V} \cdot \cos(2 \pi f_{\rm N} t )\hspace{0.05cm},$$
- $$v_2(t) = 1 \;{\rm V} \cdot \cos(2 \pi f_{\rm N} t + 1 \;{\rm V} \cdot \sin(2 \pi f_{\rm N} t) \hspace{0.05cm},$$
- $$v_3(t)= 1.5 \;{\rm V} \cdot \cos(2 \pi f_{\rm N} t) - 0.3 \;{\rm V} \cdot \cos(6 \pi f_{\rm N} t)\hspace{0.05cm}.$$
Anzumerken ist, dass hier die in der Praxis stets vorhandenen Rauschanteile als vernachlässigbar klein angenommen werden.
Hinweise:
- Die Aufgabe gehört zum Kapitel Qualitätskriterien.
- Bezug genommen wird insbesondere auf die Seite Signal-zu-Stör-Leistungsverhältnis und auf das Kapitel Nichtlineare Verzerrungen im Buch „Lineare zeitinvariante Systeme”.
- Bei nichtlinearen Verzerrungen ist das Sinken–SNR $ρ_v = 1/K^2,$ wobei der Klirrfaktor $K$ das Verhältnis der Effektivwerte aller Oberwellen zum Effektivwert der Grundfrequenz angibt.
Fragebogen
Musterlösung
- Das System $S_1$ könnte durchaus ein ideales System sein, nämlich dann, wenn für alle Frequenzen $f_{\rm N}$ die Bedingung $v(t) = q(t)$ erfüllt wäre.
- Auch die zweite Alternative ist möglich, da das ideale System ein Sonderfall der verzerrungsfreien Systeme darstellt.
- Würde bei einer anderen Nachrichtenfrequenz $f_{\rm N} \ne 1$ kHz die Bedingung $v(t) = q(t)$ allerdings nicht erfüllt, so würde ein linear verzerrendes System vorliegen, dessen Frequenzgang bei der Frequenz $f_{\rm N}$ zufällig gleich 1 wäre.
- Dagegen kann ein nichtlinear verzerrendes System (Vorschlag 4) aufgrund fehlender Oberwellen ausgeschlossen werden.
(2) Entsprechend den Ausführungen im Kapitel „Harmonische Schwingung” im Buch „Signaldarstellung” gelten folgende Gleichungen:
- $$A \cdot \cos(\omega_{\rm N} t ) + B \cdot \sin(\omega_{\rm N} t ) = C \cdot \cos(\omega_{\rm N} t - \varphi)\hspace{0.3cm} \Rightarrow \hspace{0.3cm} C = \sqrt{A^2 + B^2},\hspace{0.5cm}\varphi ={\rm arctan}\hspace{0.1cm} ({A}/{B})\hspace{0.05cm}$$
Angewandt auf das vorliegende Beispiel erhält man
- $$C = \sqrt{(1 \,{\rm V})^2 + (1 \,{\rm V})^2}= 1.414\,{\rm V}\hspace{0.05cm}.$$
Der Dämpfungsfaktor des Systems hat somit den Wert $α = 1.414/2 \hspace{0.15cm}\underline{= 0.707}$, und für die Phase gilt:
- $$ \varphi ={\rm arctan}\hspace{0.1cm}\frac {1 \,{\rm V}}{1 \,{\rm V}} = 45^{\circ} = {\pi}/{4}\hspace{0.05cm}.$$
Die Umformung $\cos(\omega_{\rm N} t - \varphi)= \cos[\omega_{\rm N} (t - \tau)]$ erlaubt Aussagen über die Laufzeit:
- $$\tau =\frac {\varphi}{2\pi f_{\rm N}} = \frac {\pi /4}{2\pi f_{\rm N}} = \frac {1}{8 \cdot 1 \,{\rm kHz}} \hspace{0.15cm}\underline {= 125\,{\rm \mu s}}\hspace{0.05cm}.$$
(3) Richtig sinddie Lösungsvorschläge 2 und 3:
- Das System $S_2$ ist nach den Ausführungen zur Teilaufgabe (1) weder ideal noch nichtlinear verzerrend.
- Dagegen sind die Alternativen 2 und 3 möglich, je nachdem, ob die berechneten Werte von $α$ und $τ$ für alle Frequenzen erhalten bleiben oder nicht.
- Mit einer einzigen Messung bei nur einer Frequenz kann allerdings diese Frage nicht geklärt werden.
(4) Das Signal $v_3(t)$ beinhaltet eine Oberwelle dritter Ordnung. Deshalb ist die Verzerrung nichtlinear ⇒ Lösungsvorschlag 2.
(5) Mit den Amplituden $A_1 = 1.5 \ \rm V$ und $A_3 = -0.3\ \rm V$ erhält man für den Klirrfaktor:
- $$ K_3 =\frac {|A_3|}{|A_1|} = 0.2\hspace{0.05cm}.$$
Deshalb beträgt das Sinken–SNR entsprechend der angegebenen Gleichung $ρ_{v3} = 1/K_3^{ 2 } = 25$.
Zum gleichen Ergebnis kommt man nach der allgemeinen Berechnung. Aus den Amplituden von Quellensignal und Grundwelle des Sinkensignals erhält man für den frequenzunabhängigen Dämpfungsfaktor:
- $$ \alpha =\frac {1.5 \,{\rm V}}{2 \,{\rm V}} = 0.75\hspace{0.05cm}.$$
Das von den nichtlinearen Verzerrungen herrührende Fehlersignal lautet deshalb: $\varepsilon_3(t) = v_3(t) - \alpha \cdot q(t) = - 0.3 \,{\rm V} \cdot \cos(6 \pi f_{\rm N} t)\hspace{0.05cm}.$ Damit ergibt sich die Verzerrungsleistung:
- $$P_{\varepsilon 3}= {1}/{2} \cdot (0.3 \,{\rm V})^2 = 0.045 \,{\rm V}^2\hspace{0.05cm}.$$
Mit der Leistung des Quellensignals, $$P_{q}= {1}/{2} \cdot (2\,{\rm V})^2 = 2 \,{\rm V}^2\hspace{0.05cm},$$ erhält man unter Berücksichtigung des gerade berechneten Dämpfungsfaktors $ \alpha = 0.75 $:
- $$\rho_{v3} = \frac{\alpha^2 \cdot P_{q}}{P_{\varepsilon 3}} = \frac{0.75^2 \cdot 2 {\rm V}^2}{0.045 } \hspace{0.15cm}\underline {= 25}\hspace{0.05cm}.$$