Difference between revisions of "Modulation Methods/Non-Linear Digital Modulation"
| Line 156: | Line 156: | ||
Die Grafik zeigt das Blockschaltbild zur Erzeugung einer MSK–Modulation und typische Signalverläufe an verschiedenen Punkten des MSK–Senders. [[File:P_ID1732__Mod_T_4_4_S6.png | right|frame| Blockschaltbild zur Erzeugung eines MSK–Signals]] | Die Grafik zeigt das Blockschaltbild zur Erzeugung einer MSK–Modulation und typische Signalverläufe an verschiedenen Punkten des MSK–Senders. [[File:P_ID1732__Mod_T_4_4_S6.png | right|frame| Blockschaltbild zur Erzeugung eines MSK–Signals]] | ||
Man erkennt | Man erkennt | ||
| − | *das digitale Quellensignal am Punkt '''(1)''', eine Folge von Diracimpulsen im Abstand $T$, gewichtet mit den Koeffizienten $a_ν ∈ \{–1, +1\}$: | + | *das digitale Quellensignal am Punkt '''(1)''', eine Folge von Diracimpulsen im Abstand $T$, gewichtet mit den Koeffizienten $a_ν ∈ \{–1, +1\}$: |
:$$q_\delta(t) = \sum_{\nu = - \infty}^{+\infty}a_{ \nu} \cdot \delta (t - \nu | :$$q_\delta(t) = \sum_{\nu = - \infty}^{+\infty}a_{ \nu} \cdot \delta (t - \nu | ||
\cdot T)\hspace{0.05cm},$$ | \cdot T)\hspace{0.05cm},$$ | ||
| − | *das Rechtecksignal $q_{\rm R}(t)$ am Punkt '''(2)''' nach Faltung mit dem Rechteckimpuls $g(t)$ der Dauer $T$ und der Höhe $1/T$: | + | *das Rechtecksignal $q_{\rm R}(t)$ am Punkt '''(2)''' nach Faltung mit dem Rechteckimpuls $g(t)$ der Dauer $T$ und der Höhe $1/T$: |
:$$q_{\rm R}(t) = \sum_{\nu = - \infty}^{+\infty}a_{ \nu} \cdot g (t - \nu | :$$q_{\rm R}(t) = \sum_{\nu = - \infty}^{+\infty}a_{ \nu} \cdot g (t - \nu | ||
\cdot T)\hspace{0.05cm},$$ | \cdot T)\hspace{0.05cm},$$ | ||
| − | *den [[Modulationsverfahren/Frequenzmodulation_(FM)#Signalverl.C3.A4ufe_bei_Frequenzmodulation|Frequenzmodulator]] (Integrator und nachgeschalteter Phasenmodulator). Für das Signal am Punkt '''(3)''' gilt: | + | *den [[Modulationsverfahren/Frequenzmodulation_(FM)#Signalverl.C3.A4ufe_bei_Frequenzmodulation|Frequenzmodulator]] (Integrator und nachgeschalteter Phasenmodulator). Für das Signal am Punkt '''(3)''' gilt: |
:$$\phi(t) = {\pi}/{2}\cdot \int_{0}^{t} | :$$\phi(t) = {\pi}/{2}\cdot \int_{0}^{t} | ||
q_{\rm R}(\tau)\hspace{0.1cm} {\rm d}\tau \hspace{0.05cm}.$$ | q_{\rm R}(\tau)\hspace{0.1cm} {\rm d}\tau \hspace{0.05cm}.$$ | ||
| − | + | <br clear=all> | |
| − | + | Die Phasenwerte bei Vielfachen der Symboldauer $T$ sind Vielfache von $π/2$, wobei der für MSK gültige Modulationsindex $h = 0.5$ berücksichtigt ist. Der Phasenverlauf ist linear. Daraus ergibt sich das MSK–Signal am Punkt '''(4)''' des Blockschaltbildes zu | |
| − | |||
| − | Die Phasenwerte bei Vielfachen der Symboldauer $T$ sind Vielfache von $π | ||
:$$s(t) = s_0 \cdot \cos (2 \pi f_{\rm T} \hspace{0.05cm}t + | :$$s(t) = s_0 \cdot \cos (2 \pi f_{\rm T} \hspace{0.05cm}t + | ||
\phi(t)) = s_0 \cdot \cos (2 \pi \cdot t \cdot (f_{\rm T}+a_{ \nu} \cdot {\rm \Delta}f_{\rm A} )) \hspace{0.05cm}.$$ | \phi(t)) = s_0 \cdot \cos (2 \pi \cdot t \cdot (f_{\rm T}+a_{ \nu} \cdot {\rm \Delta}f_{\rm A} )) \hspace{0.05cm}.$$ | ||
| Line 174: | Line 172: | ||
==Realisierung der MSK als Offset–QPSK== | ==Realisierung der MSK als Offset–QPSK== | ||
<br> | <br> | ||
| − | Durch einen modifizierten Betrieb von [[Modulationsverfahren/Quadratur–Amplitudenmodulation#Offset.E2.80.93Quadraturamplitudenmodulation|Offset–QPSK]] (O–QPSK) lässt sich auch ''Minimum Shift Keying'' (MSK) realisieren. | + | Durch einen modifizierten Betrieb von [[Modulationsverfahren/Quadratur–Amplitudenmodulation#Offset.E2.80.93Quadraturamplitudenmodulation|Offset–QPSK]] (O–QPSK) lässt sich auch ''Minimum Shift Keying'' (MSK) realisieren. |
[[File: P_ID1733__Mod_T_4_4_S7_neu.png | center|frame| Herkömmliches O–QPSK und O–QPSK in MSK–Betriebsart]] | [[File: P_ID1733__Mod_T_4_4_S7_neu.png | center|frame| Herkömmliches O–QPSK und O–QPSK in MSK–Betriebsart]] | ||
Gegenüber dem herkömmlichen Offset–QPSK–Betrieb (obere Grafik) sind folgende Modifikationen zu berücksichtigen, die in der unteren Grafik rot hervorgehoben sind: | Gegenüber dem herkömmlichen Offset–QPSK–Betrieb (obere Grafik) sind folgende Modifikationen zu berücksichtigen, die in der unteren Grafik rot hervorgehoben sind: | ||
| − | *Die Symboldauer $T$ der MSK ist gleich der Bitdauer $T_{\rm B}$ des binären Eingangssignals, während bei der originären O–QPSK $T = 2 T_{\rm B}$ gilt. | + | *Die Symboldauer $T$ der MSK ist gleich der Bitdauer $T_{\rm B}$ des binären Eingangssignals, während bei der originären O–QPSK $T = 2 T_{\rm B}$ gilt. |
| − | *Anstelle der Seriell–Parallel–Wandlung und Signalraumzuordnung müssen nun die Quellensymbole entsprechend $a_k = (–1)^{k+1} · a_{k–1} · q_k$ umcodiert werden. | + | *Anstelle der Seriell–Parallel–Wandlung und Signalraumzuordnung müssen nun die Quellensymbole entsprechend $a_k = (–1)^{k+1} · a_{k–1} · q_k$ umcodiert werden. |
| − | *Alle Amplitudenkoeffizienten $a_k$ mit geradzahligem Index ( | + | *Alle Amplitudenkoeffizienten $a_k$ mit geradzahligem Index $(a_0, a_2$, ...$)$ werden dem Diracpuls im oberen Zweig eingeprägt, während $a_1, a_3$, ... im unteren Zweig übertragen werden. |
| − | *Der Abstand der einzelnen Diracimpulse beträgt nun $2T$ anstelle von $T$ und der Versatz („Offset”) im Quadraturzweig ist nicht mehr $T/2$, sondern $T$. In beiden Fällen ist aber der Offset gleich $T_{\rm B}$. | + | *Der Abstand der einzelnen Diracimpulse beträgt nun $2T$ anstelle von $T$ und der Versatz („Offset”) im Quadraturzweig ist nicht mehr $T/2$, sondern $T$. In beiden Fällen ist aber der Offset gleich $T_{\rm B}$. |
| − | *Während beim herkömmlichen O–QPSK–Betrieb jeder beliebige Grundimpuls $g_s(t)$ möglich ist, zum Beispiel ein Rechteck– oder ein Wurzel–Nyquist–Impuls, gibt es für den MSK–Betrieb nur einen einzigen geeigneten Grundimpuls. Dieser erstreckt sich über zwei Symboldauern: | + | *Während beim herkömmlichen O–QPSK–Betrieb jeder beliebige Grundimpuls $g_s(t)$ möglich ist, zum Beispiel ein Rechteck– oder ein Wurzel–Nyquist–Impuls, gibt es für den MSK–Betrieb nur einen einzigen geeigneten Grundimpuls. Dieser erstreckt sich über zwei Symboldauern: |
:$$g_{\rm MSK}(t) = \left\{ \begin{array}{l} s_0 \cdot \cos (\frac{\pi \cdot t}{2 \cdot T}) \\ | :$$g_{\rm MSK}(t) = \left\{ \begin{array}{l} s_0 \cdot \cos (\frac{\pi \cdot t}{2 \cdot T}) \\ | ||
0 \\ \end{array} \right.\quad | 0 \\ \end{array} \right.\quad | ||
| Line 195: | Line 193: | ||
[[File:P_ID1734__Mod_T_4_4_S7b_neu.png |right|frame| Signalverläufe der O–QPSK im MSK–Betrieb]] | [[File:P_ID1734__Mod_T_4_4_S7b_neu.png |right|frame| Signalverläufe der O–QPSK im MSK–Betrieb]] | ||
{{GraueBox|TEXT=$\text{Beispiel 2:}$ Die Grafik zeigt | {{GraueBox|TEXT=$\text{Beispiel 2:}$ Die Grafik zeigt | ||
| − | *oben das binäre bipolare Quellensignal $q(t)$, | + | *oben das binäre bipolare Quellensignal $q(t)$, |
| − | *in der Mitte die äquivalenten TP–Signale $s_{\rm I}(t)$ und $s_{\rm Q}(t)$ im | + | *in der Mitte die äquivalenten TP–Signale $s_{\rm I}(t)$ und $s_{\rm Q}(t)$ im $\rm I$– und $\rm Q$–Zweig, |
| − | *unten den Phasenverlauf $ϕ(t)$ des gesamten MSK–Sendesignals $s(t)$. | + | *unten den Phasenverlauf $ϕ(t)$ des gesamten MSK–Sendesignals $s(t)$. |
| − | Die Umcodierung $a_k = (–1)^{k+1} · a_{k–1} · q_k$ ist bereits berücksichtigt, ebenso der MSK–Grundimpuls: | + | Die Umcodierung $a_k = (–1)^{k+1} · a_{k–1} · q_k$ ist bereits berücksichtigt, ebenso der MSK–Grundimpuls: |
:$$g_{\rm MSK}(t) = \left\{ \begin{array} {l} s_0 \cdot \cos (\frac{\pi \cdot t}{2 \cdot T}) \\ | :$$g_{\rm MSK}(t) = \left\{ \begin{array} {l} s_0 \cdot \cos (\frac{\pi \cdot t}{2 \cdot T}) \\ | ||
0 \\ \end{array} \right.\quad | 0 \\ \end{array} \right.\quad | ||
| Line 210: | Line 208: | ||
Man erkennt aus dem Vergleich des obersten und des untersten Diagramms: | Man erkennt aus dem Vergleich des obersten und des untersten Diagramms: | ||
| − | *Der MSK–Phasenverlauf $ϕ(t)$ ist abschnittsweise linear und steigt bzw. fällt innerhalb einer jeden Symboldauer um $90^\circ \ (π/2)$, je nachdem, ob gerade $q_k = +1$ oder $q_k = -1$ anliegt. | + | *Der MSK–Phasenverlauf $ϕ(t)$ ist abschnittsweise linear und steigt bzw. fällt innerhalb einer jeden Symboldauer um $90^\circ \ (π/2)$, je nachdem, ob gerade $q_k = +1$ oder $q_k = -1$ anliegt. |
| − | *Das Sendesignal $s(t)$ beinhaltet abschnittsweise die beiden Frequenzen $f_{\rm T} ± 1/(4T)$. Es hat prinzipiell den gleichen Verlauf wie das Signal $s_{\rm D}(t)$ im Abschnitt [[Modulationsverfahren/Nichtlineare_digitale_Modulation#Bin.C3.A4re_FSK_mit_kontinuierlicher_Phasenanpassung|Binäre FSK mit kontinuierlicher Phasenanpassung]]. | + | *Das Sendesignal $s(t)$ beinhaltet abschnittsweise die beiden Frequenzen $f_{\rm T} ± 1/(4T)$. Es hat prinzipiell den gleichen Verlauf wie das Signal $s_{\rm D}(t)$ im Abschnitt [[Modulationsverfahren/Nichtlineare_digitale_Modulation#Bin.C3.A4re_FSK_mit_kontinuierlicher_Phasenanpassung|Binäre FSK mit kontinuierlicher Phasenanpassung]]. |
| − | Diese Form der MSK–Realisierung können Sie mit dem | + | Diese Form der MSK–Realisierung können Sie mit dem interaktiven Applet [[Applets:QPSK_und_Offset-QPSK_(Applet)|Quaternary Phase Shift Keying und Offset-QPSK]] bei folgenden Einstellungen darstellen: |
*Offset–QPSK, | *Offset–QPSK, | ||
*MSK–Zuordnung, | *MSK–Zuordnung, | ||
Revision as of 14:50, 13 January 2019
Contents
- 1 Eigenschaften nichtlinearer Verfahren
- 2 FSK – Frequency Shift Keying
- 3 Kohärente Demodulation der FSK
- 4 Fehlerwahrscheinlichkeit der orthogonalen FSK
- 5 Binäre FSK mit kontinuierlicher Phasenanpassung
- 6 MSK – Minimum Shift Keying
- 7 Realisierung der MSK als Offset–QPSK
- 8 Allgemeingültige Beschreibung von Continuous Phase Modulation
- 9 GMSK – Gaussian Minimum Shift Keying
- 10 Aufgaben zum Kapitel
- 11 Quellenverzeichnis
Eigenschaften nichtlinearer Verfahren
Die Gesamtheit aller Modulationsverfahren lassen sich alternativ wie folgt klassifizieren:
- Amplituden–, Phasen– und Frequenzmodulation,
- analoge und digitale Modulationsverfahren,
- lineare und nichtlineare Modulationsverfahren.
Hinsichtlich des letzten Unterscheidungsmerkmals soll gelten:
$\text{Definition:}$ Ein lineares Modulationsverfahren liegt vor, wenn eine beliebige Linearkombination von Signalen am Modulatoreingang zu einer entsprechenden Linearkombination an dessen Ausgang führt. Andernfalls spricht man von nichtlinearer Modulation.
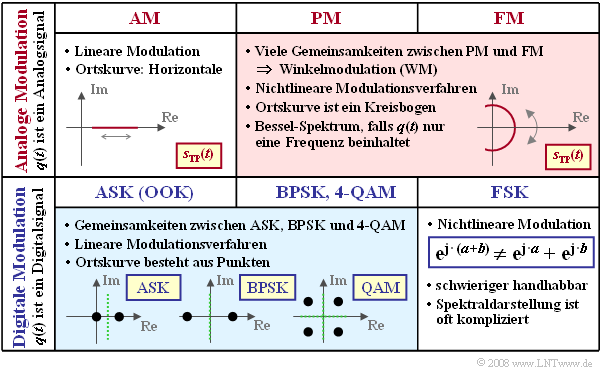
Die Grafik zeigt einige der Unterschiede hinsichtlich der oben angegebenen Klassifizierungen.
Am Kapitelanfang wurde bereits darauf hingewiesen, dass der wesentliche Unterschied zwischen einem analogen und einem digitalen Modulationsverfahren darin besteht, dass beim ersten ein analoges Quellensignal $q(t)$ anliegt und beim zweiten ein Digitalsignal. Bei genauerer Betrachtung wird man jedoch feststellen, dass es zwischen diesen Verfahren noch einige Unterschiede mehr gibt. Darauf wird im Folgenden genauer eingegangen.
- Die analoge Amplitudenmodulation (AM) ist ein lineares Modulationsverfahren. Die Ortskurve – also das äquivalente Tiefpass–Signal $s_{\rm TP}(t)$ dargestellt in der komplexen Ebene – ist eine Gerade.
- Zwischen der analogen Phasenmodulation (PM) und der analogen Frequenzmodulation (FM) gibt es viele Gemeinsamkeiten ⇒ gemeinsame Beschreibung als Winkelmodulation (WM). Hier ist die Ortskurve ein Kreisbogen. Bei einer harmonischen Schwingung gibt es ein Linienspektrum $S(f)$ bei Vielfachen der Nachrichtenfrequenz $f_{\rm N}$ um die Trägerfrequenz $f_{\rm T}$.
- Die digitale Amplitudenmodulation, die man entweder als Amplitude Shift Keying (ASK) oder als On–Off–Keying (OOK) bezeichnet, ist ebenfalls linear. Die Ortskurve besteht im binären Fall nur noch aus zwei Punkten.
- Da sich die binäre Phasenmodulation (Binary Phase Shift Keying, BPSK) als ASK mit bipolaren Amplitudenkoeffizienten darstellen lässt, ist diese ebenfalls linear. Die Form des BPSK–Leistungsdichtespektrums wird wesentlich durch das Betragsquadratspektrum $|G_s(f)|^2$ des Sendegrundimpulses bestimmt.
- Das bedeutet aber auch: Die Spektralfunktion der BPSK ist im Gegensatz zur analogen Phasenmodulation einer harmonischen Schwingung (nur eine Frequenz!) kontinuierlich in $f$. Würde man die BPSK als (analoge) Phasenmodulation mit digitalem Quellensignal $q(t)$ betrachten, so müssten zur Berechnung von ${\it Φ}_s(f)$ unendlich viele Bessel–Linienspektren miteinander gefaltet werden, wenn man $Q(f)$ als unendliche Summe von Einzelfrequenzen darstellt.
- Da die Quadratur–Amplitudenmodulation mit vier Signalraumpunkten (4–QAM) auch als Summe zweier zueinander orthogonaler und damit quasi–unabhängiger BPSK–Systeme beschrieben werden kann, stellt auch diese ein lineares Modulationsverfahren dar. Gleiches gilt für die höherstufigen QAM–Verfahren wie 16–QAM, 64–QAM, ...
- Eine höherstufige PSK, zum Beispiel die 8–PSK, ist nur in Sonderfällen linear, siehe [Klo01][1]. Die digitale Frequenzmodulation (Frequency Shift Keying, FSK) ist stets nichtlinear. Dieses Verfahren wird nachfolgend beschrieben, wobei wir uns auf die binäre FSK beschränken.
FSK – Frequency Shift Keying
Wir gehen hier aus vom Sendesignal der analogen Frequenzmodulation,
- $$s(t) = s_0 \cdot \cos\hspace{-0.05cm}\big [\psi(t)\big ] \hspace{0.2cm} {\rm mit} \hspace{0.2cm} \psi(t) = 2\pi f_{\rm T} \hspace{0.05cm}t + K_{\rm FM} \cdot \int q(t)\hspace{0.1cm} {\rm d}t,$$
sowie dem rechteckförmigen Binärsignal mit $a_ν ∈ \{+1, –1\}$ ⇒ bipolare Signalisierung:
- $$q(t) = \sum_{\nu = - \infty}^{+\infty}a_{ \nu} \cdot g_s (t - \nu \cdot T) \hspace{0.2cm} {\rm mit} \hspace{0.2cm} g_s(t) = \left\{ \begin{array}{l} A \\ 0 \\ \end{array} \right.\quad \begin{array}{*{5}c}{\rm{f\ddot{u}r}} \\{\rm{f\ddot{u}r}} \\ \end{array}\begin{array}{*{10}c} 0 < t < T\hspace{0.05cm}, \\ {\rm sonst} \hspace{0.05cm}. \\ \end{array}$$
Fasst man die Amplitude $A$ und die Modulatorkonstante $K_{\rm FM}$ zum Frequenzhub (Definition siehe unten)
- $${\rm \Delta}f_{\rm A} = \frac{A \cdot K_{\rm FM}}{2 \pi}$$
zusammen, so lautet das FSK–Sendesignal im $ν$–ten Zeitintervall:
- $$s(t) = s_0 \cdot \cos\hspace{-0.05cm}\big [2 \pi \cdot t \cdot (f_{\rm T}+a_{ \nu} \cdot {\rm \Delta}f_{\rm A} ) \big ]\hspace{0.05cm}.$$
Dieses lässt sich mit den beiden möglichen Signalfrequenzen
- $$f_{\rm +1} = f_{\rm T} +{\rm \Delta}f_{\rm A} \hspace{0.05cm}, \hspace{0.2cm}f_{\rm -1} = f_{\rm T} -{\rm \Delta}f_{\rm A}$$
auch in folgender Form schreiben:
- $$s(t) = \left\{ \begin{array}{l} s_0 \cdot \cos (2 \pi \cdot f_{\rm +1} \cdot t ) \\ s_0 \cdot \cos (2 \pi \cdot f_{\rm -1} \cdot t ) \\ \end{array} \right.\quad \begin{array}{*{5}c}{\rm{f\ddot{u}r}} \\{\rm{f\ddot{u}r}} \\ \end{array}\begin{array}{*{10}c} a_{ \nu} = +1 \hspace{0.05cm}, \\ a_{ \nu} = -1\hspace{0.05cm}. \\ \end{array}$$
Zu jedem Zeitpunkt tritt also stets nur eine der beiden Frequenzen $f_{+1}$ und $f_{–1}$ auf. Die Trägerfrequenz $f_{\rm T}$ selbst kommt im Signal nicht vor.
$\text{Definition:}$ Der Frequenzhub $Δf_{\rm A}$ ist in gleicher Weise definiert wie bei der analogen Frequenzmodulation, nämlich als die maximale Abweichung der Augenblicksfrequenz $f_{\rm A}(t)$ von der Trägerfrequenz $f_{\rm T}$. Häufig wird der Frequenzhub in der Literatur auch mit $Δf$ bzw. $F$ bezeichnet.
Eine weitere wichtige Beschreibungsgröße ist in diesem Zusammenhang der Modulationsindex, der ebenfalls bereits bei der analogen Frequenzmodulation als $η = Δf_{\rm A}/f_{\rm N}$ definiert wurde. Bei der FSK ist eine etwas andere Definition erforderlich, was hier durch einen anderen Kennbuchstaben berücksichtigt wird: $η ⇒ h$.
$\text{Definition:}$ Bei digitaler Frequenzmodulation (FSK) bezeichnet der Modulationsindex $h$ das Verhältnis aus dem Gesamtfrequenzhub und der Symbolrate $1/T$:
- $$h = \frac{2 \cdot {\rm \Delta}f_{\rm A} }{1/T} = 2 \cdot {\rm \Delta}f_{\rm A}\cdot T \hspace{0.05cm}.$$
Manchmal wird in der Fachliteratur $h$ auch als Phasenhub bezeichnet.
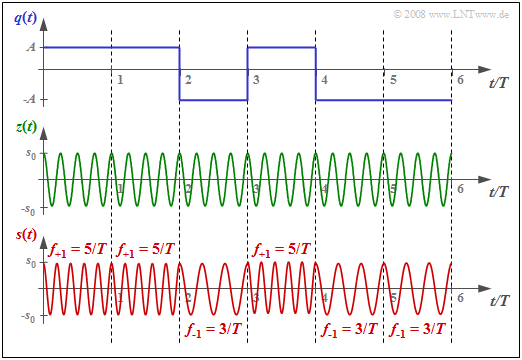
$\text{Beispiel 1:}$ Die Grafik zeigt unten das FSK–Sendesignal $s(t)$ für
- das oben skizzierte binäre Quellensignal $q(t)$ mit Amplitudenwerten $\pm A =\pm 1 \ \rm V$, und
- das darunter gezeichnete Trägersignal $z(t)$ mit vier Schwingungen pro Symboldauer $(f_{\rm T} · T = 4)$.
Zugrunde liegt der Frequenzhub $Δf_{\rm A} = 1/T$ ⇒ Modulationsindex $h = 2$. Die beiden möglichen Frequenzen sind $f_{\rm +1} = 5/T \hspace{0.05cm},\hspace{0.2cm}f_{\rm -1} = 3/T \hspace{0.05cm}.$
Bei einem FSK–Übertragungssystem mit der Bitrate $1 \ {\rm Mbit/s} \ (T = 1 \ \rm µ s)$ müsste somit die folgende FM–Konstante verwendet werden:
- $$K_{\rm FM} = \frac{2 \pi \cdot {\rm \Delta}f_{\rm A} }{A } = \frac{2 \pi }{A \cdot T } \approx 6.28 \cdot 10^{6}\,\,{\rm V^{-1}s^{-1} }\hspace{0.05cm}.$$
Kohärente Demodulation der FSK
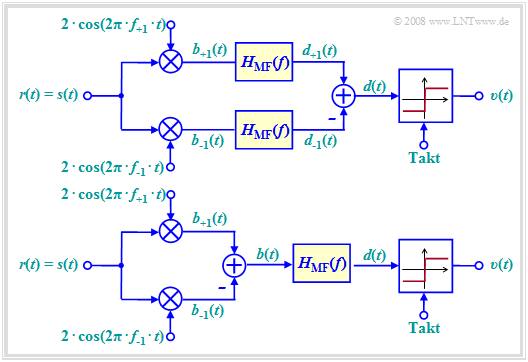
Die folgende Grafik zeigt den bestmöglichen Demodulator für binäre FSK, der kohärent arbeitet und demzufolge auch Kenntnis über die Phasenlage des FSK–Signals benötigt. Im Blockschaltbild ist dies berücksichtigt, indem das Empfangssignal $r(t)$ identisch mit dem Sendesignal $s(t)$ angenommen wurde – siehe Signalverläufe im vorherigen Abschnitt.
Dieser Demodulator arbeitet nach folgendem Prinzip:
- Es handelt sich hierbei um einen Maximum–Likelihood–Empfänger (ML) in der Realisierungsform mit Matched–Filter. Dieses Filter mit dem Frequenzgang $H_{\rm MF}(f)$ kann bei dem vorausgesetzten rechteckförmigen Sendegrundimpuls $g_s(t)$ auch als Integrator realisiert werden.
- Die Signale $b_{+1}(t)$ bzw. $b_{–1}(t)$ vor den Matched–Filtern ergeben sich durch die phasenrichtige Multiplikation mit den Schwingungen der Frequenz $f_{+1}$ bzw. $f_{–1}$.
- Der Maximum–Likelihood–Empfänger entscheidet sich bekanntlich für den Zweig (das Symbol) mit der größeren „Metrik”, wobei das nachgeschaltete Matched–Filters zu berücksichtigen ist. Das heißt: Wahrscheinlich wurde $a_ν = +1$ gesendet, wenn folgende Relation erfüllt ist:
- $$d_{\rm +1}(\nu \cdot T) > d_{\rm -1}(\nu \cdot T) \hspace{0.3cm}\Rightarrow \hspace{0.3cm} d(\nu \cdot T) = d_{\rm +1}(\nu \cdot T) - d_{\rm -1}(\nu \cdot T) > 0\hspace{0.05cm}.$$
- Das obere Blockschaltbild wurde zum besseren Verständnis in dieser Weise gezeichnet. Natürlich kann man die Matched–Filterung aber auch auf die rechte Seite der Differenzbildung verschieben, wie im unteren Modell dargestellt. Damit muss nur noch ein Filter realisiert werden.
In der Aufgabe 4.13 wird dieser FSK–Demodulator ausführlich behandelt. Auf dem entsprechenden Angabenblatt sehen Sie auch die Signalverläufe.
Fehlerwahrscheinlichkeit der orthogonalen FSK
$\text{Definition:}$ Man spricht von orthogonaler FSK,
- wenn der Modulationsindex $h$ ein ganzzahliges Vielfaches von $0.5$ ist, und damit
- der Frequenzhub $Δf_{\rm A}$ ein ganzzahliges Vielfaches von $0.25/T$.
Beim kohärenten Demodulator ist der Korrelationskoeffizient zwischen $d_{+1}(T_{\rm D})$ und $d_{–1}(T_{\rm D})$ zu allen Detektionszeitpunkten gleich Null. Der Betrag $|d(T_{\rm D})|$ – also der Abstand der Detektionsabtastwerte von der Schwelle – ist somit konstant. Es treten keine Impulsinterferenzen auf.
Geht man von den Voraussetzungen
- orthogonale FSK,
- AWGN–Kanal (gekennzeichnet durch den Quotienten $E_{\rm B}/N_0)$, und
- der hier beschriebenen kohärenten Demodulation
aus, so ergibt sich die Bitfehlerwahrscheinlichkeit zu:
- $$p_{\rm B} = {\rm Q}\left ( \sqrt{\frac{E_{\rm B}}{N_0 }} \hspace{0.1cm}\right ) = {1}/{2}\cdot {\rm erfc}\left ( \sqrt{\frac{E_{\rm B}}{2 \cdot N_0 }} \hspace{0.1cm}\right ).$$
Dies entspricht gegenüber der BPSK einer Degradation von $3 \ \rm dB$, weil
- zwar der kohärente FSK–Demodulator bezüglich des Nutzsignals das gleiche Ergebnis liefert,
- auch die Rauschleistungen in den beiden Zweigen genau so groß sind wie bei der BPSK,
- es aber wegen der Subtraktion zu einer Verdopplung der Gesamtrauschleistung kommt.
Während aber bei der BPSK eine nichtkohärente Demodulation auf keinen Fall möglich ist, gibt es auch einen nichtkohärenten FSK–Demodulator, allerdings mit etwas erhöhter Fehlerwahrscheinlichkeit:
- $$p_{\rm B} = {1}/{2} \cdot {\rm e}^{- E_{\rm B}/{(2N_0) }}\hspace{0.05cm}.$$
Die Herleitung dieser Gleichung erfolgt im Kapitel Trägerfrequenzsysteme mit nichtkohärenter Demodulation des Buches „Digitalsignalübertragung”.
Binäre FSK mit kontinuierlicher Phasenanpassung
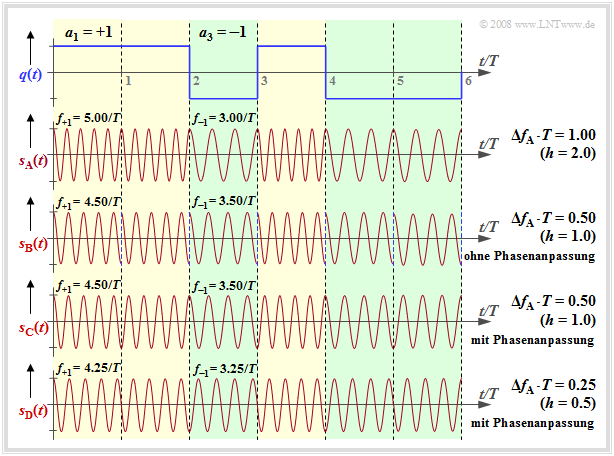
Wir betrachten weiter die orthogonale FSK. Die Grafik zeigt oben das Quellensignal $q(t)$ und und darunter gezeichnet das FSK–Signal $s_{\rm A}(t)$ mit dem Frequenzhub $Δf_{\rm A} = 1/T$ ⇒ Modulationsindex $h = 2 · Δf_{\rm A} · T = 2$.
Zu den weiteren Signalverläufen ist Folgendes anzumerken:
- Das FSK–Signal $s_{\rm B}(t)$ verwendet die Momentanfrequenzen $f_{+1} = 4.5/T$ und $f_{–1} = 3.5/T$ ⇒ $Δf_{\rm A} ·T = 0.5$ ⇒ $h = 1.$ Auch diese FSK ist orthogonal, da $h = 1$ ein Vielfaches von $0.5$ ist. Bei kleinerem $h$ ist aber die Bandbreiteneffizienz besser ⇒ das Spektrum $S_{\rm B}(f)$ ist weniger breit als das Spektrum $S_{\rm A}(f)$.
- Allerdings erkennt man im Signal $s_{\rm B}(t)$ an jeder Symbolgrenze einen Phasensprung um $π$, wodurch sich wieder eine Verbreiterung des Spektrums ergibt. Solche Phasensprünge lassen sich durch Phasenanpassung vermeiden. Man spricht dann von Continuous Phase Modulation (CPM).
- Auch beim CPM–Signal $s_{\rm C}(t)$ gilt $f_{+1} = 4.5/T, f_{–1} = 3.5/T$ und $h = 1$. Im Bereich von $0$ ... $T$ wird der Koeffizient $a_1 = +1$ mit $\cos (2π·f_{+1}·t)$ repräsentiert, im Bereich $T$ ... $2T$ wird dagegen der ebenfalls positive Koeffizient $a_2 = +1$ durch die um $π$ verschobene Funktion $\ –\cos (2π·f_{+1}·t)$ dargestellt.
- Der Modulationsindex $h = 0.5$ von Signal $s_{\rm D}(t)$ ist der kleinstmögliche Wert, der eine orthogonale FSK ermöglicht ⇒ Bezeichnung Minimum Shift Keying (MSK). Bei MSK sind bei jeder Symbolgrenze – je nach den vorherigen Symbolen – vier unterschiedliche Anfangsphasen möglich.
Zur Verdeutlichung des hier dargelegten Sachverhaltens gibt es das interaktive Applet Frequency Shift Keying & Continuous Phase Modulation (CPM).
MSK – Minimum Shift Keying
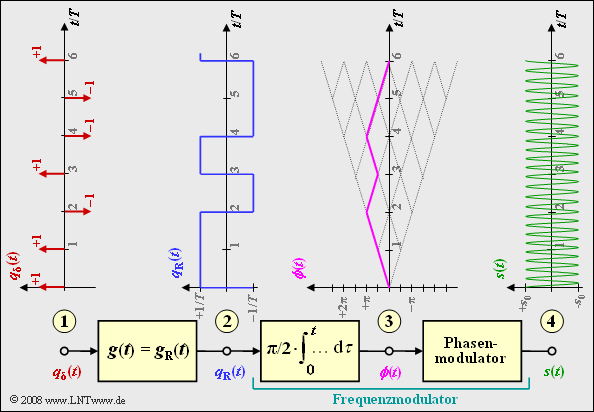
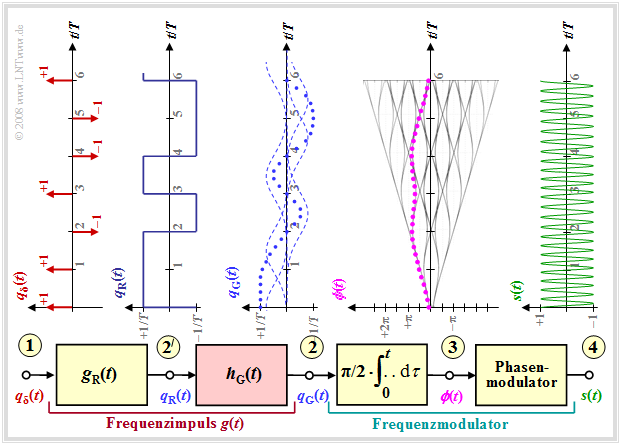
Die Grafik zeigt das Blockschaltbild zur Erzeugung einer MSK–Modulation und typische Signalverläufe an verschiedenen Punkten des MSK–Senders.
Man erkennt
- das digitale Quellensignal am Punkt (1), eine Folge von Diracimpulsen im Abstand $T$, gewichtet mit den Koeffizienten $a_ν ∈ \{–1, +1\}$:
- $$q_\delta(t) = \sum_{\nu = - \infty}^{+\infty}a_{ \nu} \cdot \delta (t - \nu \cdot T)\hspace{0.05cm},$$
- das Rechtecksignal $q_{\rm R}(t)$ am Punkt (2) nach Faltung mit dem Rechteckimpuls $g(t)$ der Dauer $T$ und der Höhe $1/T$:
- $$q_{\rm R}(t) = \sum_{\nu = - \infty}^{+\infty}a_{ \nu} \cdot g (t - \nu \cdot T)\hspace{0.05cm},$$
- den Frequenzmodulator (Integrator und nachgeschalteter Phasenmodulator). Für das Signal am Punkt (3) gilt:
- $$\phi(t) = {\pi}/{2}\cdot \int_{0}^{t} q_{\rm R}(\tau)\hspace{0.1cm} {\rm d}\tau \hspace{0.05cm}.$$
Die Phasenwerte bei Vielfachen der Symboldauer $T$ sind Vielfache von $π/2$, wobei der für MSK gültige Modulationsindex $h = 0.5$ berücksichtigt ist. Der Phasenverlauf ist linear. Daraus ergibt sich das MSK–Signal am Punkt (4) des Blockschaltbildes zu
- $$s(t) = s_0 \cdot \cos (2 \pi f_{\rm T} \hspace{0.05cm}t + \phi(t)) = s_0 \cdot \cos (2 \pi \cdot t \cdot (f_{\rm T}+a_{ \nu} \cdot {\rm \Delta}f_{\rm A} )) \hspace{0.05cm}.$$
Realisierung der MSK als Offset–QPSK
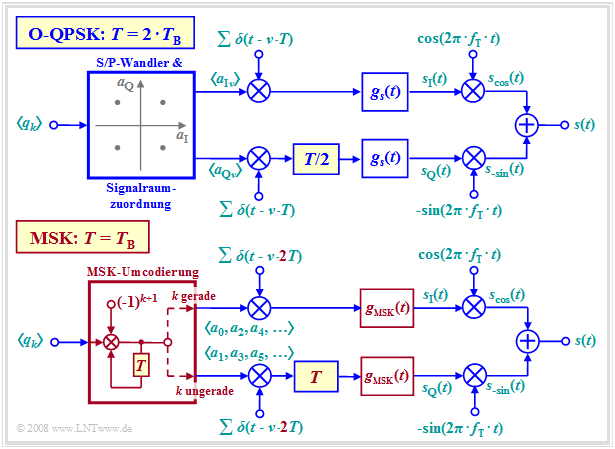
Durch einen modifizierten Betrieb von Offset–QPSK (O–QPSK) lässt sich auch Minimum Shift Keying (MSK) realisieren.
Gegenüber dem herkömmlichen Offset–QPSK–Betrieb (obere Grafik) sind folgende Modifikationen zu berücksichtigen, die in der unteren Grafik rot hervorgehoben sind:
- Die Symboldauer $T$ der MSK ist gleich der Bitdauer $T_{\rm B}$ des binären Eingangssignals, während bei der originären O–QPSK $T = 2 T_{\rm B}$ gilt.
- Anstelle der Seriell–Parallel–Wandlung und Signalraumzuordnung müssen nun die Quellensymbole entsprechend $a_k = (–1)^{k+1} · a_{k–1} · q_k$ umcodiert werden.
- Alle Amplitudenkoeffizienten $a_k$ mit geradzahligem Index $(a_0, a_2$, ...$)$ werden dem Diracpuls im oberen Zweig eingeprägt, während $a_1, a_3$, ... im unteren Zweig übertragen werden.
- Der Abstand der einzelnen Diracimpulse beträgt nun $2T$ anstelle von $T$ und der Versatz („Offset”) im Quadraturzweig ist nicht mehr $T/2$, sondern $T$. In beiden Fällen ist aber der Offset gleich $T_{\rm B}$.
- Während beim herkömmlichen O–QPSK–Betrieb jeder beliebige Grundimpuls $g_s(t)$ möglich ist, zum Beispiel ein Rechteck– oder ein Wurzel–Nyquist–Impuls, gibt es für den MSK–Betrieb nur einen einzigen geeigneten Grundimpuls. Dieser erstreckt sich über zwei Symboldauern:
- $$g_{\rm MSK}(t) = \left\{ \begin{array}{l} s_0 \cdot \cos (\frac{\pi \cdot t}{2 \cdot T}) \\ 0 \\ \end{array} \right.\quad \begin{array}{*{5}c}{\rm{f\ddot{u}r}} \\{\rm{f\ddot{u}r}} \\ \end{array}\begin{array}{*{10}c} -T \le t \le +T \hspace{0.05cm}, \\ {\rm sonst}\hspace{0.05cm}. \\ \end{array}$$
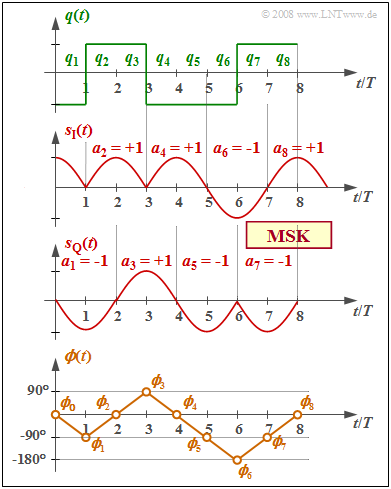
$\text{Beispiel 2:}$ Die Grafik zeigt
- oben das binäre bipolare Quellensignal $q(t)$,
- in der Mitte die äquivalenten TP–Signale $s_{\rm I}(t)$ und $s_{\rm Q}(t)$ im $\rm I$– und $\rm Q$–Zweig,
- unten den Phasenverlauf $ϕ(t)$ des gesamten MSK–Sendesignals $s(t)$.
Die Umcodierung $a_k = (–1)^{k+1} · a_{k–1} · q_k$ ist bereits berücksichtigt, ebenso der MSK–Grundimpuls:
- $$g_{\rm MSK}(t) = \left\{ \begin{array} {l} s_0 \cdot \cos (\frac{\pi \cdot t}{2 \cdot T}) \\ 0 \\ \end{array} \right.\quad \begin{array}{*{5}c}{\rm{f\ddot{u}r} } \\{\rm{f\ddot{u}r} } \\ \end{array}\begin{array}{*{10}c} -T \le t \le +T \hspace{0.05cm}, \\ {\rm sonst}\hspace{0.05cm}. \\ \end{array}$$
Man erkennt aus dem Vergleich des obersten und des untersten Diagramms:
- Der MSK–Phasenverlauf $ϕ(t)$ ist abschnittsweise linear und steigt bzw. fällt innerhalb einer jeden Symboldauer um $90^\circ \ (π/2)$, je nachdem, ob gerade $q_k = +1$ oder $q_k = -1$ anliegt.
- Das Sendesignal $s(t)$ beinhaltet abschnittsweise die beiden Frequenzen $f_{\rm T} ± 1/(4T)$. Es hat prinzipiell den gleichen Verlauf wie das Signal $s_{\rm D}(t)$ im Abschnitt Binäre FSK mit kontinuierlicher Phasenanpassung.
Diese Form der MSK–Realisierung können Sie mit dem interaktiven Applet Quaternary Phase Shift Keying und Offset-QPSK bei folgenden Einstellungen darstellen:
- Offset–QPSK,
- MSK–Zuordnung,
- Cosinusimpuls.
Allgemeingültige Beschreibung von Continuous Phase Modulation
Wir gehen weiter davon aus, dass die Quelle durch die Amplitudenkoeffizienten $a_ν$ charakterisiert wird. Diese können sowohl binär als auch $M$–stufig sein. Sie sind aber stets bipolar zu betrachten, zum Beispiel $a_ν\in \{+1, -1\}$.
- Die Phasenfunktion $ϕ(t)$ kann bei Continuous Phase Modulation (CPM) allgemein in folgender Form dargestellt werden $(h$ bezeichnet wieder den Modulationsindex):
- $$\phi(t) = {\pi}\cdot h \cdot\int_{-\infty}^{t} \sum_{\nu = - \infty}^{+\infty}a_{ \nu} \cdot g (\tau - \nu \cdot T)\hspace{0.1cm} {\rm d}\tau \hspace{0.05cm}.$$
- In dieser Darstellung bezeichnet $g(t)$ den Frequenzimpuls, der folgende Bedingung erfüllen muss:
- $$\int_{-\infty}^{+\infty} g (t)\hspace{0.1cm} {\rm d}t = 1 \hspace{0.05cm}.$$
- Mit dem Phasenimpuls $g_ϕ(t)$ gilt aber auch der folgende Zusammenhang:
- $$\phi(t) = {\pi}\cdot h \cdot \sum_{\nu = - \infty}^{+\infty}a_{ \nu} \cdot g_\phi (t - \nu \cdot T),\hspace{0.2cm}{\rm wobei}\hspace{0.2cm}g_\phi(t) = \int_{-\infty}^{t} g (\tau )\hspace{0.1cm} {\rm d}\tau\hspace{0.05cm}.$$
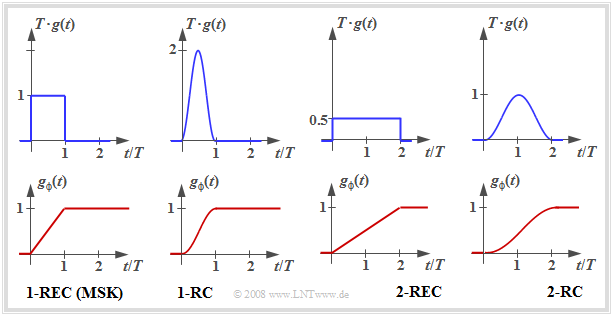
Durch geeignete Wahl der Impulse $g(t)$ bzw. $g_ϕ(t)$ lassen sich viele CPM–Varianten realisieren. Einige davon sind nachfolgend dargestellt. Die Grafik zeigt jeweils oben den CPM–Frequenzimpuls $g(t)$ und unten den CPM–Phasenimpuls $g_ϕ(t)$. Die linken Grafiken beschreiben die MSK. Die Bezeichnung „1–REC” gibt an, dass $g(t)$ sich über eine einzige Symboldauer $(T)$ erstreckt und rechteckförmig ist.
Die weiteren dargestellten CPM–Varianten wurden mit dem Ziel entworfen, die bereits kleine Bandbreite des MSK–Signals weiter zu verringern:
- Bei „1–RC” ergibt sich allein durch den „weicheren” Raised–Cosine–Impuls $g(t)$ gegenüber dem Rechteck ein schmaleres Leistungsdichtespektrum.
- Bei „2–RC” und „2–REC” handelt es sich um Partial–Response–Impulse, die sich jeweils über $2T$ erstrecken. Hierdurch wird der Phasenverlauf ebenfalls weicher.
- Dadurch wird aber auch die Demodulation erschwert, da in das Datensignal gezielte Pseudomehrstufigkeiten eingebracht werden.
- Die Berechnung der CPM–Verfahren im Spektralbereich ist im allgemeinen kompliziert. Nur der Sonderfall „MSK” führt zu einfach handhabbaren Gleichungen, wie in der Aufgabe A4.14 gezeigt wird.
$\text{Fazit:}$ Die Continuous Phase Modulation (CPM) ist keine Phasenmodulation, sondern stellt eine nichtlineare digitale Frequenzmodulation (FSK) dar, mit dem Ziel
- eine konstante Betragseinhüllende zu garantieren (Einbrüche der Hüllkurve führen schon bei geringen Nichtlinearitäten zu Problemen), und
- einen stetigen Phasenverlauf zu ermöglichen (Phasensprünge verbreitern das Spektrum).
Für genauere Informationen verweisen wir auf die Fachliteratur, zum Beispiel auf das empfehlenswerte Buch [Kam04][2].
GMSK – Gaussian Minimum Shift Keying
Ein Vorteil der MSK ist der geringe Bandbreitenbedarf, weil: Bandbreite ist stets teuer. Durch eine geringfügige Modifikation hin zum Gaussian Minimum Shift Keying (GMSK) wird das Spektrum weiter verschmälert. Diese Modulationsart wird zum Beispiel beim Mobilfunkstandard GSM angewendet.
Aus der Grafik erkennt man:
- Der Frequenzimpuls $g(t)= g_{\rm G}(t)$ ist nun nicht mehr rechteckförmig wie $g_{\rm R}(t)$, sondern weist flachere Flanken auf.
- Dadurch ergibt sich ein weicherer Phasenverlauf am Punkt (3) als bei MSK, bei dem $ϕ(t)$ symbolweise linear ansteigt bzw. abfällt.
- Man erreicht die sanfteren GMSK–Phasenübergänge durch einen Gaußtiefpass. Dessen Frequenzgang und Impulsantwort lauten mit der systemtheoretischen Grenzfrequenz $f_{\rm G}$:
- $$H_{\rm G}(f) = {\rm e}^{-\pi\cdot (\frac{f}{2 \cdot f_{\rm G}})^2} \hspace{0.2cm}\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ\, \hspace{0.2cm} h_{\rm G}(t) = 2 f_{\rm G} \cdot {\rm e}^{-\pi\cdot (2 \cdot f_{\rm G}\cdot t)^2}\hspace{0.05cm}.$$
- Der resultierende Frequenzimpuls $g(t)$ am Punkt (2) ergibt sich aus der Faltung von $g_{\rm R}(t)$ und $h_{\rm G}(t)$.
- Das Signal $s(t)$ am Punkt (4) weist bei GMSK nun nicht mehr abschnittsweise (je Symboldauer) eine konstante Frequenz auf wie bei MSK, auch wenn dies aus obiger Grafik mit bloßem Auge schwer zu erkennen ist.
$\text{Beispiel 3:}$ Beim GSM–Verfahren ist die 3dB–Grenzfrequenz mit $f_{\rm 3dB} = 0.3/T$ spezifiziert, wobei zwischen der systemtheoretischen und der 3dB–Grenzfrequenz folgender Zusammenhang besteht:
- $$H_{\rm G}(f= f_{\rm 3 \hspace{0.03cm}dB}) = {\rm e}^{-\pi\cdot ({f_{\rm 3 \hspace{0.03cm}{dB} } }/{2 f_{\rm G} })^2} = {1}/{\sqrt{2} }\hspace{0.15cm}\Rightarrow\hspace{0.15cm} f_{\rm 3 dB} = f_{\rm G} \cdot \sqrt { {4}/{\pi}\cdot {\rm ln }\sqrt{2} }\approx {2}/{3}\cdot f_{\rm G} \hspace{0.05cm}.$$
Aus $f_{\rm 3dB} = 0.3/T$ folgt damit auch $f_{\rm G} · T ≈ 0.45$.
Aufgaben zum Kapitel
Aufgabe 4.13: FSK–Demodulation
Aufgabe 4.14: Phasenverlauf der MSK
Aufgabe 4.14Z: Offset–QPSK vs. MSK
Aufgabe 4.15: MSK im Vergleich mit BPSK und QPSK
Aufgabe 4.15Z: MSK–Grundimpuls und MSK-Spektrum
Aufgabe 4.16: Vergleich zwischen binärer PSK und binärer FSK
Quellenverzeichnis