Modulation Methods/Further OFDM Applications

1. Modulation Methods
2. Vielfachzugriffsverfahren
3. Further OFDM Applications

• Previous page
• Next page

• Previous page
• Next page

OFDM bei DVB–T

DVB–T  (Digital Video Broadcasting Terrestrial)  ist eine von mehreren aus dem DVB–Standard von 1997 abgeleitete Variante für die Verbreitung von Fernsehsignalen in digitaler Form. Andere damit verwandte Standards sind:

• DVB–S   ⇒   für die Übertragung über Satellit,
• DVB–C   ⇒   für die Übertragung über das Kabelnetz (Cable),
• DVB–H   ⇒   für mobile Geräte (Handhelds).

In Deutschland konnten ab Ende 2008 schon mehr als 90% der Bevölkerung zumindest eine Auswahl öffentlich–rechtlicher Sender über DVB–T empfangen. Seit 2017 ist der analoge Fernsehempfang über Antenne endgültig nicht mehr möglich. Die durch die Abschaltung der Analogübertragung frei gewordenen Frequenzbänder wurden durch DVB–T direkt wiederverwendet, so dass ein Parallelbetrieb und damit ein „sanfter” Übergang nicht möglich war.

Bei DVB–T kommt das Modulationsverfahren  Coded Orthogonal Frequency Division Multiplex – abgekürzt COFDM – zum Einsatz. Die Erweiterung um eine Vorwärtsfehlerkorrektur (Forward Error Correction, FEC) in Verbindung mit der bereits eingeführten Guard–Intervall–Technik ist notwendig, um den durch Echos (Mehrwegeempfang) und die Empfängerbewegung (Doppler–Effekt) entstandenen Störungen entgegenzuwirken.

Grundsätzlich handelt es sich bei DVB–T um ein Gleichwellennetz. Im Gegensatz zu klassischen Mobilfunknetzen – zum Beispiel dem GSM–Netz – werden hierbei selbst von direkt benachbarten Sendestationen die gleichen Frequenzen wiederverwendet. Dies führt an den Zellgrenzen zu Interferenzen zwischen ähnlich starken Signalen, die jedoch erhebliche Laufzeitunterschiede aufweisen können.

Den Auswirkungen eines solchen frequenzselektiven Kanals kann zwar durch eine Verlängerung des Guard–Intervalls entgegengewirkt werden. Jedoch wird dadurch zum einen die Bandbreiteneffizienz verringert, zum anderen auch die Anfälligkeit gegenüber zeitvarianten Effekten erhöht.

Systemparameter von DVB–T

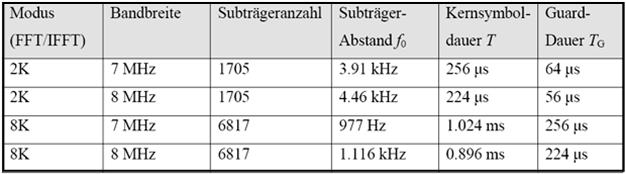
Die alten, analog genutzten Fernsehkanäle hatten jeweils eine Bandbreite von  $\text{7 MHz}$  (VHF, Very High Frequency   ⇒   Ultrakurzwelle) bzw. von  $\text{8 MHz}$  (UHF, Ultra High Frequency   ⇒   Dezimeterwelle). Ein jeder dieser Kanäle wird bei DVB–T meist mit vier Programmen belegt. Dafür wird das zur Verfügung stehende Spektrum auf die OFDM–Unterträger aufgeteilt.

Die folgende Tabelle zeigt mögliche Parameterkonstellationen eines DVB–T–Systems. Als „Modus” wird die Anzahl der für die FFT/IFFT verwendeten Stützstellen bezeichnet, also  $\text{2048 (2K)}$  bzw.  $\text{8192 (8K)}$. Es werden aber nicht alle Träger tatsächlich genutzt.

Parameter bei DVB-T

Ein Vergleich der beiden Modi zeigt, dass

• der 2K–Betrieb wegen der kürzeren Kernsymboldauer  $T$  für zeitvariante Einsatzbedingungen zwar gut geeignet ist,
• aber aufgrund der recht kurzen Guard–Intervalldauer  $T_{\rm G}$  der tolerierbaren Kanalimpulsantwort enge Grenzen gesetzt sind.

Im 8K–Modus ist dies genau umgekehrt. Wegen der Forderung eines Gleichwellennetzes ist demnach der 8K– dem 2K–Betrieb vorzuziehen, wobei jedoch der Nachteil einer aufwändigeren Implementierung der FFT/IFFT in Kauf genommen werden muss.

Für die Modulation der Unterträger stehen bei DVB–T drei QAM–Varianten zur Verfügung:

• 4–QAM (dieses Verfahren kann auch als eine 4–PSK aufgefasst werden),
• 16–QAM (optional mit asymmetrischer Signalraumkonstellation),
• 64–QAM (ebenfalls optional mit asymmetrischer Signalraumkonstellation).

Eine asymmetrische Signalraumkonstellation erlaubt eine hierarchische Quellencodierung. Bei schlechten Übertragungsbedingungen kann statt dem exakten Signalraumpunkt lediglich der Quadrant detektiert werden. Damit ist der Empfang weiterhin möglich, wenn auch bei (stark) verminderter Bildqualität.

In der folgernden Tabelle aus WIKIPEDIA sind einige resultierende Datenraten für DVB–T abhängig von der Kanalcodierungsrate  $R_{\rm C}$  und der Dauer  $T_{\rm G}$  des Guard–Intervalls angegeben. Die relative Coderedundanz beträgt  $1 - R_{\rm C}$. Das heißt:   Je größer die Coderate  $R_{\rm C}$  ist, desto weniger Redundanz wird hinzugefügt.

Nettobitraten bei DVB-T. Quelle:   https://de.wikipedia.org/wiki/DVB-T#Technik

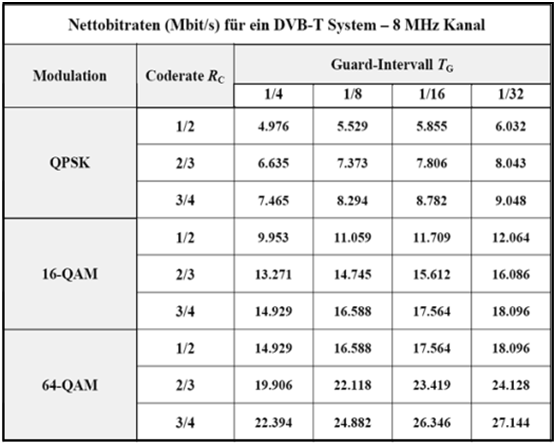
Die Zahlenwerte lassen sich wie folgt interpretieren:

• Die effektiven Nettobitraten variieren zwischen den einzelnen Sendegebieten stark, da je nach Region unterschiedliche Systemparameter verwendet werden müssen. Im Mittel werden in etwa  $12$ ...  $\text{20 Mbit/s}$  erreicht. Damit wird nun ein MPEG-2-Transportstrom übertragen, der in der Regel vier Programme enthält.

• Die Videodatenströme bei DVB–T sind in Deutschland ebenfalls MPEG–2 codiert und erreichen jeweils eine Datenrate von ca.  $\text{3.5 Mbit/s}$. Im Vergleich dazu würde ein digitalisiertes PAL–Signal bereits einer Datenrate von  $3$ ... $\text{5 Mbit/s}$ entsprechen. Eine DVD käme immerhin schon auf ca.  $\text{9.8 Mbit/s}$.

• Seit 2009 gibt es mit DVB–T2 einen Standard, der neben anderen Modifikationen zum Beispiel auch MPEG–4 anstelle von MPEG–2 verwendet. DVB–T2 ereicht gegenüber DVB–T eine deutlich bessere Bildqualität.

Eine Kurzbeschreibung von DSL – Digital Subscriber Line

Als ein weiteres Beispiel für den Einsatz von OFDM soll nun ein kurzer Überblick über  DSL  (Digital Subscriber Line) gegeben werden:

• Die DSL–Technik ermöglicht eine erhebliche Erhöhung der Datenübertragungsrate im Vergleich zu herkömmlichen Telefonanschlüssen wie  POTS  (Plain Old Telephone Service) oder  ISDN  (Integrated Services Digital Network), ohne dass für diese neue Technologie die Kupfer–Doppeladern der Teilnehmeranschlussleitung ausgetauscht werden mussten.
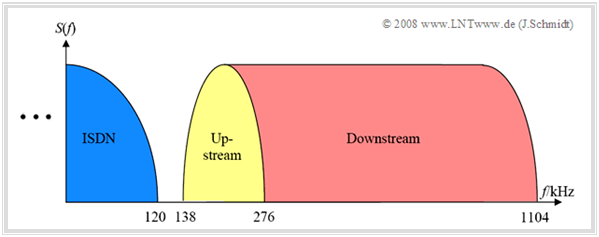
• POTS oder ISDN können auch ohne Einschränkungen parallel zu DSL betrieben werden, da sich die verwendeten Frequenzbänder bei entsprechender Anpassung nicht überschneiden (siehe Grafik).

ADSL–over–ISDN

Es existieren folgende wesentliche xDSL–Varianten („x” ist hierbei als Platzhalter zu verstehen):

• ADSL (Asymmetric Digital Subscriber Line),
• ADSL2+, eine Erweiterung zu ADSL,
• VDSL/VDSL2 (Very High Data Rate Digital Subscriber Line).

VDSL2 ist auf maximale symmetrische Datenraten (jeweils  $\text{210 Mbit/s}$ im Up– und Downstream) ausgelegt, aber nur über kurze Leitungen realisierbar.

Als Modulationsverfahren wird bei allen diesen xDSL–Varianten stets OFDM verwendet, das in diesem Zusammenhang häufig auch den Namen DMT (Discrete Multitone Transmission) trägt. Betrachten wir beispielsweise die DMT bei ADSL mit folgenden Kenngrößen:

• Grundfrequenz  $f_0 = 4.3125\ \rm kHz$,
• maximale Nutzträgerzahl:  $N = 255$,
• gleichsignalfrei, da  $S(f = 0) = 0$  ist,
• der Nyquist-Tone   ⇒   $S(256 · f_0)$  wird ebenfalls zu Null gesetzt,
• maximale Frequenz:   $256 · 4.3125 \ \rm kHz = 1104 \ \rm kHz$.

Es ergibt sich die in der obigen Abbildung gezeigte Belegung des Spektrums. Eine genaue Systembeschreibung findet man im Kapitel   DSL  des LNTwww–Buches „Beispiele von Nachrichtensystemen”.

Das dargestellte Sendespektrum von DSL lässt sich in aller Kürze wie folgt beschreiben:

• Die $224$ für DMT verfügbaren Träger – diese bezeichnet man im Zusammenhang mit der DMT oft auch als Bins – werden entweder für den Upstream $($Übertragung ins Netz,  $32$ Bins,  $\text{138 kHz)}$ oder den Downstream $($Übertragung aus dem Netz,  $192$ Bins,  $\text{828 kHz)}$ verwendet.
• Alle ADSL–Anschlüsse der Deutschen Telekom sind nach dem Standard ADSL–over–ISDN geschaltet, so dass ein Parallelbetrieb zu ISDN möglich ist. Dafür wird der Frequenzbereich bis  $\text{138 kHz}$  nicht für ADSL verwendet und die entsprechenden Bins zu Null gesetzt.
• Auch bei den analogen Anschlüssen wird ADSL–over–ISDN und nicht ADSL–over–POTS eingesetzt, obwohl dadurch gerade jener Frequenzbereich verschwendet wird, der eine besonders günstige Kabeldämpfung aufweist.

Der wesentliche Vorteil von DSL bzw. DMT liegt wieder in der Anpassungsfähigkeit an den Kanal. Die im Zugangsnetz verwendeten Kupfer–Doppeladern haben unter anderem wegen des Skin–Effekts keinen idealen Dämpfungs– und Phasengang. Die DMT bietet wieder je nach Güte des Frequenzbereichs der Bins die Möglichkeit, das jeweilige Modulationsverfahren anzupassen oder sogar auf die Nutzung eines Trägers ganz zu verzichten.

Auch bei DSL kommt die Guard–Intervall–Technik in Form des zyklischen Präfixes zum Einsatz. Zur Fehlervermeidung kann zusätzlich Interleaving verwendet werden, wodurch jedoch die Übertragung verzögert wird. Der Verzicht auf diese Technik wird mit dem Begriff Fast–Path bezeichnet.

$\text{Fazit:}$  Auch im Bereich der leitungsgebundenen Übertragungstechnik ermöglichte erst der Übergang vom Einträgersystem hin zu einem Mehrträgersystem die heute üblichen hohen Übertragungsraten.

Unterschiede zwischen DMT und dem beschriebenen OFDM

Die OFDM–Systembeschreibungen in den Kapiteln  Allgemeine Beschreibung von OFDM  sowie   Realisierung von OFDM-Systemen  gelten nur für Bandpass–Systeme, die hier stets im äquivalenten Tiefpassbereich betrachtet wurden:

• Durch die Tiefpass–Transformation werden alle Anteile bei negativen Frequenzen entfernt, was zu einer unsymmetrischen Spektralfunktion und damit zu einem komplexwertigen Zeitsignal führt.
• Bei DSL ist diese Tiefpass–Transformation nicht nötig, da es im Gegensatz zu Mobilfunksystemen im Basisband betrieben wird.

Dies führt zu einer abweichenden Formelrepräsentation. Für eine klare Abgrenzung zwischen den beiden Betrachtungsweisen verwenden wir im Folgenden „OFDM” nur für ein Bandpass-System, während sich die Bezeichnung „DMT” stets auf ein Basisband–System bezieht.

DMT-Spektrum

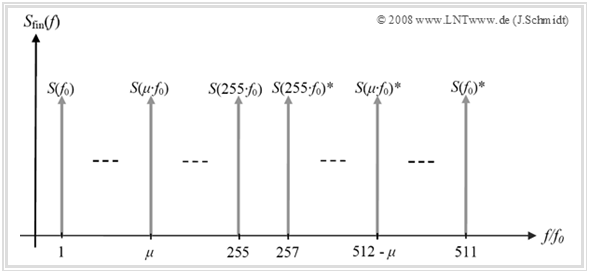
Die Grafik zeigt das diskrete Spektrum eines DMT–Signals mit  $255$  verwendeten Trägern (Bins). Das Spektrum der Nutzträger von $1$ bis $255$ wird um die auch bei den entsprechenden negativen Frequenzen anliegenden Anteile nach der unten stehenden Gleichung ergänzt, um eine Periode des für die IDFT benötigten „finiten Spektrums” zu erhalten. Für dieses Spektrum gilt nach [Han08]:

$$S(-\mu \cdot f_0 ) = S\big[(N - \mu ) \cdot f_0 \big] = S(\mu \cdot f_0)^*,$$

wobei allgemein  $0 < \mu < N/2$  und für die Grafik  $N = 512$  gilt.

Das somit rein reelle Zeitsignal ergibt sich nach der inversen diskreten Fouriertransformation an den Abtastzeitpunkten  $ν · T_{\rm A}$  mit  $0 ≤ ν < N$  und  $T_{\rm A} = T/N$  zu:

$$s_\nu = \sum\limits_{\mu = 0}^{N - 1} {S(\mu \cdot f_0 ) \cdot {\rm{e}}^{{\kern 1pt} {\rm j \hspace{0.03cm}\cdot \hspace{0.03cm}2\pi } \hspace{0.03cm}\cdot \hspace{0.03cm}\nu \hspace{0.03cm}\cdot \hspace{0.03cm}\mu /{N}} }.$$

$\text{Fazit:}$  Die benötigte Anzahl der Frequenzstützstellen und Abtastwerte der IDFT/DFT entspricht beim DMT–Verfahren dem Zweifachen der nutzbaren Träger, wenn der Gleichanteil sowie der Nyquistton vernachlässigt werden, und ist damit auch doppelt so groß wie bei einem OFDM–Bandpass–System.

$\text{Beispiel 1:}$  Es gelte  $N = 512$  und  $S(64 · f_0) = (a + {\rm j} · b)/2$  und  $S(448 · f_0) = S^{\star}(64 · f_0) = (a - {\rm j} · b)/2$. Alle anderen Spektralkoeffizienten seien  $0$.

(1)  Wir berechnen nun nach der angegebenen Formel mittels IDFT die Zeitbereichskoeffizienten:

$$\begin{align*}s_\nu & = \sum\limits_{\mu = 0}^{N - 1} {S (\mu \cdot f_0 ) \cdot {\rm{e} }^{ {\rm{j \hspace{0.03cm}\cdot \hspace{0.03cm}2 \pi } } \hspace{0.03cm}\cdot \hspace{0.03cm} \nu \hspace{0.03cm}\cdot \hspace{0.03cm}\mu /{N} } } =S( 64 \cdot f_0 ) \cdot {\rm{e} }^{ {\rm{j \hspace{0.03cm}\cdot \hspace{0.03cm}2 \pi } } \hspace{0.03cm}\cdot \hspace{0.03cm} \nu \hspace{0.03cm}\cdot \hspace{0.03cm}64 /512} + S( 448 \cdot f_0 ) \cdot {\rm{e} }^{ {\rm{j \hspace{0.03cm}\cdot \hspace{0.03cm}2 \pi } } \hspace{0.03cm}\cdot \hspace{0.03cm} \nu \hspace{0.03cm}\cdot \hspace{0.03cm}448 /512} = \\ & = {1}/ {2} \cdot (a + {\rm{j} } \cdot b ) \cdot {\rm{e} }^{ {\rm{j \hspace{0.03cm}\cdot \hspace{0.03cm}2 \pi } } \hspace{0.03cm}\cdot \hspace{0.03cm} \nu \hspace{0.03cm}\cdot \hspace{0.03cm}64 /512} + {1}/{2} \cdot (a - {\rm{j} } \cdot b ) \cdot {\rm{e} }^{ {\rm{j \hspace{0.03cm}\cdot \hspace{0.03cm}2 \pi } } \hspace{0.03cm}\cdot \hspace{0.03cm} \nu \hspace{0.03cm}\cdot \hspace{0.03cm}448 /512}.\end{align*}$$

(2)  Wendet man hierauf den  Satz von Euler  an, so erhält man:

$$s_\nu = \frac{a + {\rm{j} } \cdot b } {2} \cdot \left[ {\rm{cos} } ( 2\pi \cdot \frac{ {64} } { {512} }\cdot \nu ) + {\rm{j} } \cdot {\rm{sin} } ( 2\pi \cdot \frac{ {64} } { {512} }\cdot \nu ) \right] + \frac{a - {\rm{j} } \cdot b } {2} \cdot \left[ {\rm{cos} } ( 2\pi \cdot \frac{ {448} } { {512} }\cdot \nu ) + {\rm{j} } \cdot {\rm{sin} } ( 2\pi \cdot \frac{ {448} } { {512} }\cdot \nu )\right].$$

Dabei gilt:

$${\rm{cos} } ( 2\pi \cdot \frac{ {448} } { {512} }\cdot \nu ) = {\rm{cos} } ( 2\pi \cdot \frac{ {64} } { {512} }\cdot \nu ), \qquad {\rm{sin} } ( 2\pi \cdot \frac{ {448} } { {512} }\cdot \nu ) = - {\rm{sin} } ( 2\pi \cdot \frac{ {64} } { {512} }\cdot \nu ).$$

(3)  Durch Zusammenfassen ergeben sich hier rein reelle Zeitsignalkoeffizienten:

$$s_\nu = a \cdot {\rm{cos} } ( 2\pi \cdot \frac{ {64} } { {512} }\cdot \nu ) - b \cdot {\rm{sin} } ( 2\pi \cdot \frac{ {64} } { {512} }\cdot \nu ).$$

• Der Parameter  $a$  stellt dabei die Inphase–Komponente der QAM–Modulation des jeweiligen Trägers (Bins) dar.
• Der Parameter  $b$  gibt die Quadratur–Komponente an.

In gleicher Weise kann für die anderen „Trägerpaare” vorgegangen werden.

Aufgabe zum Kapitel

Aufgabe 5.10: DMT–Verfahren bei DSL