Difference between revisions of "Aufgaben:Exercise 1.08: Comparison of ASK and BPSK"
m (Textersetzung - „*Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.“ durch „ “) |
|||
| Line 3: | Line 3: | ||
}} | }} | ||
| − | [[File:P_ID1680__Dig_A_4_1.png|right|frame| | + | [[File:P_ID1680__Dig_A_4_1.png|right|frame|Bitfehlerwahrscheinlichkeiten <br>von ASK und BPSK]] |
| − | Die Bitfehlerwahrscheinlichkeiten der Modulationsarten ''Amplitude Shift Keying'' (ASK) und ''Binary Shift Keying'' (BPSK) werden oft durch die beiden folgenden Gleichungen angegeben: | + | Die Bitfehlerwahrscheinlichkeiten der Modulationsarten ''Amplitude Shift Keying'' (ASK) und ''Binary Shift Keying'' (BPSK) werden oft durch die beiden folgenden Gleichungen angegeben: |
:$$p_{\rm ASK} = \ {\rm Q}\left ( \sqrt{\frac{E_{\rm B}}{N_0 }} \hspace{0.1cm}\right ) = \ {1}/{2}\cdot {\rm erfc}\left ( \sqrt{\frac{E_{\rm B}}{2 \cdot N_0 }} \right ),$$ | :$$p_{\rm ASK} = \ {\rm Q}\left ( \sqrt{\frac{E_{\rm B}}{N_0 }} \hspace{0.1cm}\right ) = \ {1}/{2}\cdot {\rm erfc}\left ( \sqrt{\frac{E_{\rm B}}{2 \cdot N_0 }} \right ),$$ | ||
:$$ p_{\rm BPSK} = \ {\rm Q}\left ( \sqrt{\frac{2 \cdot E_{\rm B}}{N_0 }} \hspace{0.1cm}\right ) = \ {1}/{2}\cdot {\rm erfc}\left ( \sqrt{\frac{E_{\rm B}}{ N_0 }} \right ).$$ | :$$ p_{\rm BPSK} = \ {\rm Q}\left ( \sqrt{\frac{2 \cdot E_{\rm B}}{N_0 }} \hspace{0.1cm}\right ) = \ {1}/{2}\cdot {\rm erfc}\left ( \sqrt{\frac{E_{\rm B}}{ N_0 }} \right ).$$ | ||
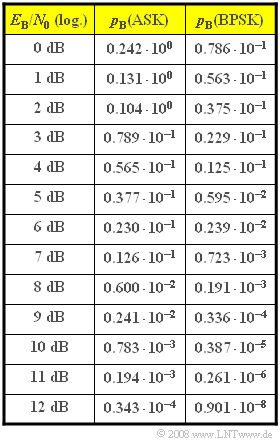
Diese beiden Gleichungen sind in der beigefügten Tabelle ausgewertet. Dabei gilt: | Diese beiden Gleichungen sind in der beigefügten Tabelle ausgewertet. Dabei gilt: | ||
| − | *$E_{\rm B}$ gibt die mittlere Energie pro Bit an. | + | *$E_{\rm B}$ gibt die mittlere Energie pro Bit an. |
| − | *$N_{0}$ ist die Rauschleistungsdichte. | + | *$N_{0}$ ist die Rauschleistungsdichte. |
| − | *Zwischen den Fehlerfunktionen ${\rm Q}(x)$ und ${\rm erfc}(x)$ besteht ein fester Zusammenhang. | + | *Zwischen den Fehlerfunktionen ${\rm Q}(x)$ und ${\rm erfc}(x)$ besteht ein fester Zusammenhang. |
| + | |||
Anzumerken ist, dass diese Gleichungen nicht allgemein gelten, sondern nur unter gewissen idealisierten Bedingungen. Diese Voraussetzungen sollen in dieser Aufgabe herausgearbeitet werden. | Anzumerken ist, dass diese Gleichungen nicht allgemein gelten, sondern nur unter gewissen idealisierten Bedingungen. Diese Voraussetzungen sollen in dieser Aufgabe herausgearbeitet werden. | ||
| + | |||
| + | |||
| + | |||
| + | |||
''Hinweise:'' | ''Hinweise:'' | ||
| − | *Die Aufgabe gehört zum Kapitel [[Digitalsignalübertragung/Lineare_digitale_Modulation_–_Kohärente_Demodulation|Lineare digitale Modulation – Kohärente Demodulation]]. | + | *Die Aufgabe gehört zum Kapitel [[Digitalsignalübertragung/Lineare_digitale_Modulation_–_Kohärente_Demodulation|Lineare digitale Modulation – Kohärente Demodulation]]. |
| − | *Sie können die Ergebnisse mit dem Applet [[Komplementäre Gaußsche Fehlerfunktionen]] überprüfen. | + | *Sie können die Ergebnisse mit dem Applet [[Applets:Komplementäre_Gaußsche_Fehlerfunktionen_(neues_Applet)|Komplementäre Gaußsche Fehlerfunktionen]] überprüfen. |
| Line 26: | Line 31: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {Welcher Zusammenhang besteht zwischen ${\rm Q}(x)$ und ${\rm erfc}(x)$? | + | {Welcher Zusammenhang besteht zwischen ${\rm Q}(x)$ und ${\rm erfc}(x)$? |
|type="[]"} | |type="[]"} | ||
| − | - Es gilt ${\rm Q}(x)= 2 \cdot{\rm erfc}(x)$, | + | - Es gilt ${\rm Q}(x)= 2 \cdot{\rm erfc}(x)$, |
| − | + Es gilt ${\rm Q}(x)= 0.5 \cdot{\rm erfc}(x)/\sqrt{2})$, | + | + Es gilt ${\rm Q}(x)= 0.5 \cdot{\rm erfc}(x)/\sqrt{2})$, |
| − | - Es gilt ${\rm erfc}(x)= 0.5 \cdot{\rm Q}(x)/\sqrt{2})$. | + | - Es gilt ${\rm erfc}(x)= 0.5 \cdot{\rm Q}(x)/\sqrt{2})$. |
| − | {Wann gelten die angegebenen | + | {Wann gelten die angegebenen Gleichungen für die Fehlerwahrscheinlichkeits? |
|type="[]"} | |type="[]"} | ||
+ Sie gelten nur für den AWGN–Kanal. | + Sie gelten nur für den AWGN–Kanal. | ||
| − | + Sie gelten nur für Matched–Filter–Empfänger (oder Varianten). | + | + Sie gelten nur für den Matched–Filter–Empfänger (oder Varianten). |
- Die Gleichungen berücksichtigen Impulsinterferenzen. | - Die Gleichungen berücksichtigen Impulsinterferenzen. | ||
- Die Gleichungen gelten nur bei rechteckförmigen Signalen. | - Die Gleichungen gelten nur bei rechteckförmigen Signalen. | ||
| − | {Wie lauten die Fehlerwahrscheinlichkeiten für $10 \cdot \lg \ E_{\rm B}/N_{0} = 12\, \rm dB$? | + | {Wie lauten die Fehlerwahrscheinlichkeiten für $10 \cdot \lg \ E_{\rm B}/N_{0} = 12\, \rm dB$? |
|type="{}"} | |type="{}"} | ||
$ p_{\rm ASK} \ = \ $ { 0.343 3% } $\ \cdot 10^{-4}$ | $ p_{\rm ASK} \ = \ $ { 0.343 3% } $\ \cdot 10^{-4}$ | ||
$ p_{\rm BPSK} \ = \ $ { 0.901 3% } $\ \cdot 10^{-8}$ | $ p_{\rm BPSK} \ = \ $ { 0.901 3% } $\ \cdot 10^{-8}$ | ||
| − | {Welche Fehlerwahrscheinlichkeiten ergeben sich für $E_{\rm B}/N_{0} = 8$? | + | {Welche Fehlerwahrscheinlichkeiten ergeben sich für $E_{\rm B}/N_{0} = 8$? |
|type="{}"} | |type="{}"} | ||
$ p_{\rm ASK} \ = \ $ { 0.241 3% } $\ \cdot 10^{-2}$ | $ p_{\rm ASK} \ = \ $ { 0.241 3% } $\ \cdot 10^{-2}$ | ||
$ p_{\rm BPSK} \ = \ $ { 0.336 3% } $\ \cdot 10^{-4}$ | $ p_{\rm BPSK} \ = \ $ { 0.336 3% } $\ \cdot 10^{-4}$ | ||
| − | {Die Fehlerwahrscheinlichkeit soll nicht größer werden als $10^{-8}$. Wie groß ist das erforderliche $10 \cdot \lg \ E_{\rm B}/N_{0}$ bei ASK? | + | {Die Fehlerwahrscheinlichkeit soll nicht größer werden als $10^{-8}$. Wie groß ist das erforderliche $10 \cdot \lg \ E_{\rm B}/N_{0}$ bei ASK? |
|type="{}"} | |type="{}"} | ||
$(E_{\rm B}/N_{0})_{\rm min} \ = \ $ { 15 3% } $\ \rm dB $ | $(E_{\rm B}/N_{0})_{\rm min} \ = \ $ { 15 3% } $\ \rm dB $ | ||
Revision as of 11:16, 6 February 2019
Die Bitfehlerwahrscheinlichkeiten der Modulationsarten Amplitude Shift Keying (ASK) und Binary Shift Keying (BPSK) werden oft durch die beiden folgenden Gleichungen angegeben:
- $$p_{\rm ASK} = \ {\rm Q}\left ( \sqrt{\frac{E_{\rm B}}{N_0 }} \hspace{0.1cm}\right ) = \ {1}/{2}\cdot {\rm erfc}\left ( \sqrt{\frac{E_{\rm B}}{2 \cdot N_0 }} \right ),$$
- $$ p_{\rm BPSK} = \ {\rm Q}\left ( \sqrt{\frac{2 \cdot E_{\rm B}}{N_0 }} \hspace{0.1cm}\right ) = \ {1}/{2}\cdot {\rm erfc}\left ( \sqrt{\frac{E_{\rm B}}{ N_0 }} \right ).$$
Diese beiden Gleichungen sind in der beigefügten Tabelle ausgewertet. Dabei gilt:
- $E_{\rm B}$ gibt die mittlere Energie pro Bit an.
- $N_{0}$ ist die Rauschleistungsdichte.
- Zwischen den Fehlerfunktionen ${\rm Q}(x)$ und ${\rm erfc}(x)$ besteht ein fester Zusammenhang.
Anzumerken ist, dass diese Gleichungen nicht allgemein gelten, sondern nur unter gewissen idealisierten Bedingungen. Diese Voraussetzungen sollen in dieser Aufgabe herausgearbeitet werden.
Hinweise:
- Die Aufgabe gehört zum Kapitel Lineare digitale Modulation – Kohärente Demodulation.
- Sie können die Ergebnisse mit dem Applet Komplementäre Gaußsche Fehlerfunktionen überprüfen.
Fragebogen
Musterlösung
- $$\rm Q (\it x) = \ \frac{\rm 1}{\sqrt{\rm 2\pi}}\int_{\it x}^{+\infty}\rm e^{\it -u^{\rm 2}/\rm 2}\,d \it u \hspace{0.05cm},$$
- $$\rm erfc (\it x) = \ \frac{\rm 2}{\sqrt{\rm \pi}}\int_{\it x}^{+\infty}\rm e^{\it -u^{\rm 2}}\,d \it u \hspace{0.05cm}.$$
Durch einfache Substitutionen kann der oben genannte Zusammenhang einfach nachgewiesen werden:
- $$\rm Q ( x) = 1/2 \cdot \rm erfc (x/\sqrt{2}) \hspace{0.05cm}.$$
(2) Richtig sind die beiden ersten Lösungsvorschläge:
- Die Gleichungen gelten nur für den AWGN–Kanal und für einen optimalen Binärempfänger, zum Beispiel entsprechend des Matched–Filter–Ansatzes.
- Impulsinterferenzen – verursacht durch den Kanal oder das Empfangsfilter – werden damit nicht erfasst.
- Die genaue Sendeimpulsformung spielt dagegen keine Rolle, solange das Empfangsfilter $H_{\rm E}(f)$ an das Sendespektrum angepasst ist. Vielmehr gilt:
- Zwei unterschiedliche Sendeimpulsformer $H_{\rm S}(f)$ führen zur genau gleichen Fehlerwahrscheinlichkeit, wenn sie die gleiche Energie pro Bit aufweisen.
(3) Diese Ergebnisse können direkt aus der Tabelle abgelesen werden:
- $$p_{\rm ASK} \hspace{0.1cm}\underline {= 0.343 \cdot 10^{-4}},\hspace{0.3cm}p_{\rm BPSK} \hspace{0.1cm}\underline {= 0.901 \cdot 10^{-8}}.$$
(4) Mit $E_{\rm B}/N_{0} = 8\ \Rightarrow \ 10 \cdot \lg \ E_{\rm B}/N_{0} \approx 9 \ \rm dB$ erhält man folgende Fehlerwahrscheinlichkeiten:
- $$p_{\rm ASK} \hspace{0.1cm}\underline {= 0.241 \cdot 10^{-2}},\hspace{0.3cm}p_{\rm BPSK} \hspace{0.1cm}\underline {= 0.336 \cdot 10^{-4}}.$$
(5) Aus der Teilaufgabe (3) folgt, dass bei der binären Phasenmodulation $10 \cdot \lg \ E_{\rm B}/N_{0} \approx 12 \ \rm dB$ erfüllt sein muss, damit $p_{\rm BPSK} \approx 10^{-8}$ möglich ist. Die angegebenen Gleichungen zeigen aber auch, dass die ASK–Kurve um $3 \ \rm dB$ (exakt $3.01 \ \rm dB$) rechts von der BPSK–Kurve liegt. Daraus folgt:
- $$10 \cdot {\rm lg}\hspace{0.1cm}(E_{\rm B}/N_{\rm 0})_{\rm min}\hspace{0.1cm}\underline {\approx 15\,\,{\rm dB}} \hspace{0.05cm}.$$