Difference between revisions of "Aufgaben:Exercise 4.2: AM/PM Oscillations"
m (Textersetzung - „\*\s*Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0\.” ein.“ durch „ “) |
|||
| Line 3: | Line 3: | ||
[[File:P_ID1997__Dig_A_4_2.png|right|frame|AM/PM-Schwingungen]] | [[File:P_ID1997__Dig_A_4_2.png|right|frame|AM/PM-Schwingungen]] | ||
| − | Wir betrachten | + | Wir betrachten die Signalmenge $\{s_i(t)\}$ mit der Laufvariablen $i = 1, \ \text{...} \, M$. Alle Signale $s_i(t)$ können in gleicher Weise dargestellt werden: |
:$$s_i(t) = | :$$s_i(t) = | ||
\left\{ \begin{array}{c} A_i \cdot \cos(2\pi f_{\rm T}t + \phi_i) \\ | \left\{ \begin{array}{c} A_i \cdot \cos(2\pi f_{\rm T}t + \phi_i) \\ | ||
| Line 10: | Line 10: | ||
\\ {\rm sonst}\hspace{0.05cm}. \\ \end{array}$$ | \\ {\rm sonst}\hspace{0.05cm}. \\ \end{array}$$ | ||
| − | Die Signaldauer $T$ ist dabei ein ganzzahliges Vielfaches von $1/f_{\rm T}$, wobei $f_{\rm T}$ die Signalfrequenz (Trägerfrequenz) angibt. | + | Die Signaldauer $T$ ist dabei ein ganzzahliges Vielfaches von $1/f_{\rm T}$, wobei $f_{\rm T}$ die Signalfrequenz (Trägerfrequenz) angibt. |
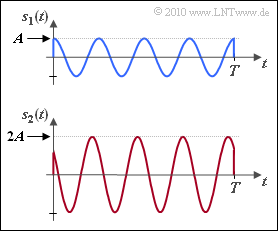
| − | Für die Skizze beträgt die Dauer der energiebegrenzten Signale jeweils $T = 4/f_{\rm T}$, das heißt, man erkennt jeweils genau vier Schwingungen innerhalb von $T$. Die einzelnen Signale $s_i(t)$ unterscheiden sich in der Amplitude ( | + | *Für die Skizze beträgt die Dauer der energiebegrenzten Signale jeweils $T = 4/f_{\rm T}$, das heißt, man erkennt jeweils genau vier Schwingungen innerhalb von $T$. |
| + | *Die einzelnen Signale $s_i(t)$ unterscheiden sich in der Amplitude $(A_i)$ und/oder der Phase $(\phi_i)$. | ||
| + | |||
| + | |||
| + | Für die beiden ersten (in der Grafik dargestellten) Signale gilt: | ||
:$$s_1(t)\hspace{-0.1cm} \ = \ \hspace{-0.1cm} A \cdot \cos(2\pi f_{\rm T}t ) \hspace{0.05cm},$$ | :$$s_1(t)\hspace{-0.1cm} \ = \ \hspace{-0.1cm} A \cdot \cos(2\pi f_{\rm T}t ) \hspace{0.05cm},$$ | ||
:$$s_2(t)\hspace{-0.1cm} \ = \ \hspace{-0.1cm} 2A \cdot \cos(2\pi f_{\rm T}t + \pi/4) \hspace{0.05cm}. $$ | :$$s_2(t)\hspace{-0.1cm} \ = \ \hspace{-0.1cm} 2A \cdot \cos(2\pi f_{\rm T}t + \pi/4) \hspace{0.05cm}. $$ | ||
| − | Beschränkt man sich zunächst auf diese beiden Signale $s_1(t)$ und $s_2(t)$, so kann man diese durch die Basisfunktionen $\varphi_1(t)$ und $\varphi_2(t)$ vollständig beschreiben. Diese sind orthonormal zueinander, das heißt, unter Berücksichtigung der Zeitbegrenzung auf $T$ gilt: | + | Beschränkt man sich zunächst auf diese beiden Signale $s_1(t)$ und $s_2(t)$, so kann man diese durch die Basisfunktionen $\varphi_1(t)$ und $\varphi_2(t)$ vollständig beschreiben. Diese sind orthonormal zueinander, das heißt, unter Berücksichtigung der Zeitbegrenzung auf $T$ gilt: |
:$$\int_{0}^{T}\varphi_1^2(t) \, {\rm d} t = \int_{0}^{T}\varphi_2^2(t) \, {\rm d} t = 1 \hspace{0.05cm}, \hspace{0.2cm} | :$$\int_{0}^{T}\varphi_1^2(t) \, {\rm d} t = \int_{0}^{T}\varphi_2^2(t) \, {\rm d} t = 1 \hspace{0.05cm}, \hspace{0.2cm} | ||
\int_{0}^{T}\varphi_1(t) \cdot \varphi_2(t)\, {\rm d} t = 0 | \int_{0}^{T}\varphi_1(t) \cdot \varphi_2(t)\, {\rm d} t = 0 | ||
| Line 25: | Line 29: | ||
:$$s_2(t)\hspace{-0.1cm} \ = \ \hspace{-0.1cm} s_{21} \cdot \varphi_1(t) + s_{22} \cdot \varphi_2(t) \hspace{0.05cm}. $$ | :$$s_2(t)\hspace{-0.1cm} \ = \ \hspace{-0.1cm} s_{21} \cdot \varphi_1(t) + s_{22} \cdot \varphi_2(t) \hspace{0.05cm}. $$ | ||
| − | In der Teilaufgabe (7) soll überprüft werden, ob sich alle Signale $s_i(t)$ gemäß der obigen Definition (mit beliebiger Amplitude $A_i$ und beliebiger Phase $\phi_i$ | + | In der Teilaufgabe '''(7)''' soll überprüft werden, ob sich alle Signale $s_i(t)$ gemäß der obigen Definition $($mit beliebiger Amplitude $A_i$ und beliebiger Phase $\phi_i)$ durch die folgende Gleichung beschreiben lassen: |
:$$s_i(t)= s_{i1} \cdot \varphi_1(t) + s_{i2} \cdot \varphi_2(t) \hspace{0.05cm}. $$ | :$$s_i(t)= s_{i1} \cdot \varphi_1(t) + s_{i2} \cdot \varphi_2(t) \hspace{0.05cm}. $$ | ||
| − | Die Basisfunktionen $\varphi_1(t)$ und $\varphi_2(t)$ sollen hier durch das [[Digitalsignal%C3%BCbertragung/Signale,_Basisfunktionen_und_Vektorr%C3%A4ume#Das_Verfahren_nach_Gram-Schmidt| Gram–Schmidt–Verfahren]] gefunden werden, das im Theorieteil ausführlich beschrieben wurde. Die erforderlichen Gleichungen sind hier nochmals zusammengestellt: | + | Die Basisfunktionen $\varphi_1(t)$ und $\varphi_2(t)$ sollen hier durch das [[Digitalsignal%C3%BCbertragung/Signale,_Basisfunktionen_und_Vektorr%C3%A4ume#Das_Verfahren_nach_Gram-Schmidt| Gram–Schmidt–Verfahren]] gefunden werden, das im Theorieteil ausführlich beschrieben wurde. Die erforderlichen Gleichungen sind hier nochmals zusammengestellt: |
:$$\varphi_1(t) = \frac{s_1(t)}{||s_1(t)||}\hspace{0.4cm}{\rm mit}\hspace{0.4cm} | :$$\varphi_1(t) = \frac{s_1(t)}{||s_1(t)||}\hspace{0.4cm}{\rm mit}\hspace{0.4cm} | ||
s_{11} = ||s_1(t)|| = \sqrt{\int_{0}^{T}s_1^2(t) \, {\rm d} t} | s_{11} = ||s_1(t)|| = \sqrt{\int_{0}^{T}s_1^2(t) \, {\rm d} t} | ||
| Line 37: | Line 41: | ||
:$$\theta_2(t) = s_2(t) - s_{21} \cdot \varphi_1(t)\hspace{0.05cm}, \hspace{0.2cm} | :$$\theta_2(t) = s_2(t) - s_{21} \cdot \varphi_1(t)\hspace{0.05cm}, \hspace{0.2cm} | ||
\varphi_2(t) = \frac{\theta_2(t)}{||\theta_2(t)||}\hspace{0.05cm}.$$ | \varphi_2(t) = \frac{\theta_2(t)}{||\theta_2(t)||}\hspace{0.05cm}.$$ | ||
| + | |||
| + | |||
| + | |||
''Hinweise:'' | ''Hinweise:'' | ||
| − | *Die Aufgabe gehört zum Kapitel [[Digitalsignal%C3%BCbertragung/Signale,_Basisfunktionen_und_Vektorr%C3%A4ume| Signale, Basisfunktionen und Vektorräume]]. | + | *Die Aufgabe gehört zum Kapitel [[Digitalsignal%C3%BCbertragung/Signale,_Basisfunktionen_und_Vektorr%C3%A4ume| Signale, Basisfunktionen und Vektorräume]]. |
| − | * Verwenden Sie zur Abkürzung die Energie $E = 1/2 \cdot A^2 \cdot T$. | + | * Verwenden Sie zur Abkürzung die Energie $E = 1/2 \cdot A^2 \cdot T$. |
| − | * Desweiteren ist folgende trigonometrische Beziehung gegeben: $\cos(\alpha \pm \beta) = \cos(\alpha )\cdot \cos(\beta) \mp \sin(\alpha )\cdot \sin(\beta)\hspace{0.05cm}.$ | + | * Desweiteren ist folgende trigonometrische Beziehung gegeben: |
| + | :$$\cos(\alpha \pm \beta) = \cos(\alpha )\cdot \cos(\beta) \mp \sin(\alpha )\cdot \sin(\beta)\hspace{0.05cm}.$$ | ||
===Fragebogen=== | ===Fragebogen=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {Wie groß ist die Energie und die 2–Norm des Signals $s_1(t)$, ausgedrückt mit $E$? | + | {Wie groß ist die Energie und die 2–Norm des Signals $s_1(t)$, ausgedrückt mit $E$? |
|type="{}"} | |type="{}"} | ||
$E_1\ = \ $ { 1 3% } $\ \cdot E$ | $E_1\ = \ $ { 1 3% } $\ \cdot E$ | ||
$||s_1(t)|| \ = \ $ { 1 3% } $\ \cdot \sqrt{E}$ | $||s_1(t)|| \ = \ $ { 1 3% } $\ \cdot \sqrt{E}$ | ||
| − | {Wie lautet die Basisfunktion $\varphi_1(t)$ nach Gram–Schmidt? | + | {Wie lautet die Basisfunktion $\varphi_1(t)$ nach Gram–Schmidt? |
|type="[]"} | |type="[]"} | ||
- $\varphi_1(t) = \sqrt{E} \cdot {\rm cos}(2\pi f_{\rm T}t)$, | - $\varphi_1(t) = \sqrt{E} \cdot {\rm cos}(2\pi f_{\rm T}t)$, | ||
| Line 59: | Line 67: | ||
+ $\varphi_1(t) = \sqrt{2/T} \cdot {\rm cos}(2\pi f_{\rm T}t)$. | + $\varphi_1(t) = \sqrt{2/T} \cdot {\rm cos}(2\pi f_{\rm T}t)$. | ||
| − | {Welcher Zusammenhang besteht zwischen $s_1(t)$ und $\varphi_1(t)$? | + | {Welcher Zusammenhang besteht zwischen $s_1(t)$ und $\varphi_1(t)$? |
|type="[]"} | |type="[]"} | ||
+ $s_1(t) = \sqrt{E} \cdot \varphi_1(t)$, | + $s_1(t) = \sqrt{E} \cdot \varphi_1(t)$, | ||
| Line 65: | Line 73: | ||
- $s_1(t) = \sqrt{2/T} \cdot \varphi_1(t)$. | - $s_1(t) = \sqrt{2/T} \cdot \varphi_1(t)$. | ||
| − | {Wie lautet das innere Produkt $s_{\rm 21} = 〈 s_2(t) \cdot \varphi_1(t)〉$? | + | {Wie lautet das innere Produkt $s_{\rm 21} = 〈 s_2(t) \cdot \varphi_1(t)〉$? |
|type="{}"} | |type="{}"} | ||
$s_{\rm 21} \ = \ $ { 1.414 3% } $\ \cdot \sqrt{E}$ | $s_{\rm 21} \ = \ $ { 1.414 3% } $\ \cdot \sqrt{E}$ | ||
| − | {Wie lautet die Hilfsfunktion $\theta_2(t)$? | + | {Wie lautet die Hilfsfunktion $\theta_2(t)$? |
|type="[]"} | |type="[]"} | ||
- $\theta_2(t) = +\sqrt{2} \cdot A \cdot {\rm sin}(2\pi f_{\rm T}t)$, | - $\theta_2(t) = +\sqrt{2} \cdot A \cdot {\rm sin}(2\pi f_{\rm T}t)$, | ||
| Line 75: | Line 83: | ||
- $\theta_2(t) = \sqrt{2/T} \cdot {\rm sin}(2\pi f_{\rm T}t)$. | - $\theta_2(t) = \sqrt{2/T} \cdot {\rm sin}(2\pi f_{\rm T}t)$. | ||
| − | {Geben Sie die Koeffizienten von $s_2(t) = s_{\rm 21} \cdot \varphi_1(t) + s_{\rm 22} \cdot \varphi_2(t)$ an. | + | {Geben Sie die Koeffizienten von $s_2(t) = s_{\rm 21} \cdot \varphi_1(t) + s_{\rm 22} \cdot \varphi_2(t)$ an. |
|type="{}"} | |type="{}"} | ||
$s_{\rm 21}\ = \ $ { 1.414 3% } $\ \cdot \sqrt{E}$ | $s_{\rm 21}\ = \ $ { 1.414 3% } $\ \cdot \sqrt{E}$ | ||
$s_{\rm 22}\ = \ $ { 1.414 3% } $\ \cdot \sqrt{E}$ | $s_{\rm 22}\ = \ $ { 1.414 3% } $\ \cdot \sqrt{E}$ | ||
| − | {Welche der Aussagen gelten allgemen für die Basisfunktionen der Signalmenge $\{s_i(t)\}$ mit $i = 1, \ \text{ ...} \ , M$, falls $M \gg 2$? | + | {Welche der Aussagen gelten allgemen für die Basisfunktionen der Signalmenge $\{s_i(t)\}$ mit $i = 1, \ \text{ ...} \ , M$, falls $M \gg 2$? |
|type="[]"} | |type="[]"} | ||
| − | - Die Anzahl der Basisfunktionen ist stets $N = M$. | + | - Die Anzahl der Basisfunktionen ist stets $N = M$. |
| − | + Die Anzahl der Basisfunktionen ist stets $N = 2$. | + | + Die Anzahl der Basisfunktionen ist stets $N = 2$. |
+ Mögliche Basisfunktionen sind Cosinus und (Minus–)Sinus. | + Mögliche Basisfunktionen sind Cosinus und (Minus–)Sinus. | ||
</quiz> | </quiz> | ||
Revision as of 08:50, 11 March 2019
Wir betrachten die Signalmenge $\{s_i(t)\}$ mit der Laufvariablen $i = 1, \ \text{...} \, M$. Alle Signale $s_i(t)$ können in gleicher Weise dargestellt werden:
- $$s_i(t) = \left\{ \begin{array}{c} A_i \cdot \cos(2\pi f_{\rm T}t + \phi_i) \\ 0 \end{array} \right.\quad \begin{array}{*{1}c} 0 \le t < T \hspace{0.05cm}, \\ {\rm sonst}\hspace{0.05cm}. \\ \end{array}$$
Die Signaldauer $T$ ist dabei ein ganzzahliges Vielfaches von $1/f_{\rm T}$, wobei $f_{\rm T}$ die Signalfrequenz (Trägerfrequenz) angibt.
- Für die Skizze beträgt die Dauer der energiebegrenzten Signale jeweils $T = 4/f_{\rm T}$, das heißt, man erkennt jeweils genau vier Schwingungen innerhalb von $T$.
- Die einzelnen Signale $s_i(t)$ unterscheiden sich in der Amplitude $(A_i)$ und/oder der Phase $(\phi_i)$.
Für die beiden ersten (in der Grafik dargestellten) Signale gilt:
- $$s_1(t)\hspace{-0.1cm} \ = \ \hspace{-0.1cm} A \cdot \cos(2\pi f_{\rm T}t ) \hspace{0.05cm},$$
- $$s_2(t)\hspace{-0.1cm} \ = \ \hspace{-0.1cm} 2A \cdot \cos(2\pi f_{\rm T}t + \pi/4) \hspace{0.05cm}. $$
Beschränkt man sich zunächst auf diese beiden Signale $s_1(t)$ und $s_2(t)$, so kann man diese durch die Basisfunktionen $\varphi_1(t)$ und $\varphi_2(t)$ vollständig beschreiben. Diese sind orthonormal zueinander, das heißt, unter Berücksichtigung der Zeitbegrenzung auf $T$ gilt:
- $$\int_{0}^{T}\varphi_1^2(t) \, {\rm d} t = \int_{0}^{T}\varphi_2^2(t) \, {\rm d} t = 1 \hspace{0.05cm}, \hspace{0.2cm} \int_{0}^{T}\varphi_1(t) \cdot \varphi_2(t)\, {\rm d} t = 0 \hspace{0.05cm}.$$
Mit diesen Basisfunktionen lassen sich die beiden Signale wie folgt darstellen:
- $$s_1(t)\hspace{-0.1cm} \ = \ \hspace{-0.1cm} s_{11} \cdot \varphi_1(t) \hspace{0.05cm},$$
- $$s_2(t)\hspace{-0.1cm} \ = \ \hspace{-0.1cm} s_{21} \cdot \varphi_1(t) + s_{22} \cdot \varphi_2(t) \hspace{0.05cm}. $$
In der Teilaufgabe (7) soll überprüft werden, ob sich alle Signale $s_i(t)$ gemäß der obigen Definition $($mit beliebiger Amplitude $A_i$ und beliebiger Phase $\phi_i)$ durch die folgende Gleichung beschreiben lassen:
- $$s_i(t)= s_{i1} \cdot \varphi_1(t) + s_{i2} \cdot \varphi_2(t) \hspace{0.05cm}. $$
Die Basisfunktionen $\varphi_1(t)$ und $\varphi_2(t)$ sollen hier durch das Gram–Schmidt–Verfahren gefunden werden, das im Theorieteil ausführlich beschrieben wurde. Die erforderlichen Gleichungen sind hier nochmals zusammengestellt:
- $$\varphi_1(t) = \frac{s_1(t)}{||s_1(t)||}\hspace{0.4cm}{\rm mit}\hspace{0.4cm} s_{11} = ||s_1(t)|| = \sqrt{\int_{0}^{T}s_1^2(t) \, {\rm d} t} \hspace{0.05cm},\hspace{0.4cm} s_{21} = \hspace{0.1cm} < \hspace{-0.1cm} s_2(t), \hspace{0.1cm}\varphi_1(t) \hspace{-0.1cm} > \hspace{0.1cm} = \int_{0}^{T}s_2(t) \cdot \varphi_1(t)\, {\rm d} t \hspace{0.05cm},$$
- $$\theta_2(t) = s_2(t) - s_{21} \cdot \varphi_1(t)\hspace{0.05cm}, \hspace{0.2cm} \varphi_2(t) = \frac{\theta_2(t)}{||\theta_2(t)||}\hspace{0.05cm}.$$
Hinweise:
- Die Aufgabe gehört zum Kapitel Signale, Basisfunktionen und Vektorräume.
- Verwenden Sie zur Abkürzung die Energie $E = 1/2 \cdot A^2 \cdot T$.
- Desweiteren ist folgende trigonometrische Beziehung gegeben:
- $$\cos(\alpha \pm \beta) = \cos(\alpha )\cdot \cos(\beta) \mp \sin(\alpha )\cdot \sin(\beta)\hspace{0.05cm}.$$
Fragebogen
Musterlösung
- $$E_{1} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \int_{0}^{T}A^2 \cdot \cos^2(2\pi f_{\rm T}t )\, {\rm d} t = \frac{A^2 \cdot T}{2}\hspace{0.05cm}+\hspace{0.05cm} \frac{A^2 }{2}\int_{0}^{T} \cos(4\pi f_{\rm T}t )\, {\rm d} t = \frac{A^2 \cdot T}{2} \hspace{0.05cm}\underline{= 1 \cdot E} \hspace{0.05cm}. $$
Hierbei ist berücksichtigt, dass $T$ ein geradzahliges Vielfaches von $1/f_{\rm T}$ ist, so dass das zweite Integral verschwindet. Weiter gilt:
- $$||s_1(t)|| = \sqrt{E_1} = \sqrt{E} = \hspace{0.1cm}\hspace{0.15cm}\underline{1 \cdot\sqrt{E}} \hspace{0.05cm}.$$
(2) Richtig ist der Lösungsvorschlag 3: Die Basisfunktion $\varphi_1(t)$ ist formgleich mit $s_1(t)$, wobei gilt:
- $$\varphi_1(t) = \frac{s_1(t)}{||s_1(t)||}= \frac{A \cdot \cos(2\pi f_{\rm T}t )}{\sqrt{E}}= \frac{A \cdot \cos(2\pi f_{\rm T}t )}{\sqrt{1/2 \cdot A^2 \cdot T}} = \sqrt{{2}/{T}} \cdot \cos(2\pi f_{\rm T}t ) \hspace{0.05cm}.$$
(3) Richtig ist der Lösungsvorschlag 1, da entsprechend der unter (2) angegebenen Gleichung gilt:
- $$s_1(t) = ||s_1(t)|| \cdot \varphi_1(t) = \sqrt{E} \cdot \varphi_1(t) \hspace{0.05cm}.$$
(4) Mit dem Signal $s_2(t)$ entsprechend der Angabe, der Basisfunktion $\varphi_1(t)$ gemäß Teilaufgabe (2) sowie der angegebenen trigonometrischen Beziehung erhält man:
- $$s_{21} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \hspace{0.1cm} < \hspace{-0.1cm} s_2(t), \hspace{0.1cm}\varphi_1(t) \hspace{-0.1cm} > \hspace{0.1cm} = \int_{0}^{T}2A \cdot \cos(2\pi f_{\rm T}t + {\pi}/{4}) \cdot \sqrt{{2}/{T}} \cdot \cos(2\pi f_{\rm T}t )\, {\rm d} t = $$
- $$\Rightarrow \hspace{0.3cm}s_{21} = \sqrt{\frac{8A^2}{T}}\cdot \int_{0}^{T}\cos({\pi}/{4}) \cdot \cos^2(2\pi f_{\rm T}t )\, {\rm d} t \hspace{0.1cm}- \sqrt{\frac{8A^2}{T}}\cdot \int_{0}^{T}\sin({\pi}/{4}) \cdot \sin(2\pi f_{\rm T}t )\cdot \cos(2\pi f_{\rm T}t )\, {\rm d} t \hspace{0.05cm}. $$
Der zweite Anteil ergibt den Wert $0$ (Orthogonalität). Der erste Anteil liefert:
- $$s_{21} = \sqrt{\frac{8A^2}{T}}\cdot \frac{1}{\sqrt{2}}\cdot \frac{T}{2} = \sqrt{A^2 \cdot T} = \sqrt{2E} \hspace{0.1cm}\hspace{0.15cm}\underline { = 1.414 \cdot \sqrt{E}} \hspace{0.05cm}.$$
(5) Entsprechend dem Gram–Schmidt–Verfahren erhält man
- $$\theta_2(t) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} s_2(t) - s_{21} \cdot \varphi_1(t)\hspace{0.05cm} = 2A \cdot \cos(2\pi f_{\rm T}t + {\pi}/{4}) - \sqrt{A^2 \cdot T} \cdot \sqrt{{2}/{T}} \cdot \cos(2\pi f_{\rm T}t ) $$
- $$\Rightarrow \hspace{0.3cm}\theta_2(t) = 2A \cdot \cos({\pi}/{4})\cdot \cos(2\pi f_{\rm T}t )\hspace{0.1cm} - \hspace{0.1cm} 2A \cdot \sin({\pi}/{4})\cdot \sin(2\pi f_{\rm T}t )\hspace{0.1cm} - \sqrt{2} \cdot A \cdot \cos(2\pi f_{\rm T}t ) \hspace{0.05cm}. $$
Mit $\cos {(\pi/4)} = \sin (\pi/4) =\sqrt{0.5}$ folgt daraus:
- $$\theta_2(t) = - \sqrt{2} \cdot A \cdot \sin(2\pi f_{\rm T}t ) \hspace{0.05cm}.$$
Richtig ist demnach der Lösungsvorschlag 2.
(6) Analog zur Teilaufgabe (2) ergibt sich die orthonormale Basisfunktion $\varphi_2(t)$ zu
- $$\varphi_2(t) = \frac{\theta_2(t)}{||\theta_2(t)||} = - \sqrt{{2}/{T}} \cdot \sin(2\pi f_{\rm T}t ) \hspace{0.05cm}.$$
Damit kann das Signal $s_2(t)$ mit $s_{21}$ entsprechend Teilaufgabe (4) wie folgt dargestellt werden:
- $$s_2(t)\hspace{-0.1cm} \ = \ \hspace{-0.1cm} s_{21} \cdot \varphi_1(t) + s_{22} \cdot \varphi_2(t) \hspace{0.05cm}, \hspace{0.2cm}s_{21} = \underline{ = 1.414 \cdot \sqrt {E}}\hspace{0.05cm},$$
- $$s_{22}\hspace{-0.1cm} \ = \ \hspace{-0.1cm} \frac{\theta_2(t)}{\varphi_2(t)} = \frac{-\sqrt{2} \cdot A \cdot \sin(2\pi f_{\rm T}t )} {-\sqrt{2/T}\cdot \sin(2\pi f_{\rm T}t )} = \sqrt{2} \cdot \sqrt{1/2 \cdot A^2 \cdot T}\hspace{0.05cm} \underline{ = 1.414 \cdot \sqrt {E}}\hspace{0.05cm}.$$
(7) Wir betrachten sehr viele energiebegrenzte Signale ($M \gg 2$) folgender Form:
- $$s_i(t)= \left\{ \begin{array}{c} A_i \cdot \cos(2\pi f_{\rm T}t + \phi_i) \\ 0 \end{array} \right.\quad \begin{array}{*{1}c} 0 \le t < T \hspace{0.05cm}, \\ {\rm sonst}\hspace{0.05cm}. \\ \end{array}$$
Die Laufvariable kann dabei die Werte $i = 1, 2, \ \text{...} \ , M$ annehmen. Dann gilt:
- Alle $M$ Signale lassen sich durch nur $N = 2$ Basisfunktionen vollständig beschreiben:
- $$s_i(t)= s_{i1} \cdot \varphi_1(t) + s_{i2} \cdot \varphi_2(t) \hspace{0.05cm}. $$
- Geht man nach dem Gram–Schmidt–Verfahren vor, so erhält man für die beiden Basisfunktionen
- $$\varphi_1(t) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \sqrt{{2}/{T}} \cdot \cos(2\pi f_{\rm T}t + \phi_1)\hspace{0.05cm},\hspace{0.5cm} \varphi_2(t) = \sqrt{{2}/{T}} \cdot \cos(2\pi f_{\rm T}t + \phi_1 \pm {\pi}/{2})\hspace{0.05cm}.$$
- Das Vorzeichen im Argument der zweiten Cosinusfunktion ($± \pi/2$) ist nicht eindeutig. Vielmehr hängt auch das Vorzeichen von $s_{i 2}$ davon ab, ob bei $\varphi_2(t)$ das Pluszeichen oder das Minuszeichen verwendet wurde.
- Mögliche Basisfunktionen, die dann zu anderen Koeffizienten führen, sind aber auch:
- $$\varphi_1(t) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \sqrt{{2}/{T}} \cdot \cos(2\pi f_{\rm T}t )\hspace{0.05cm},\hspace{0.5cm} \varphi_2(t) \pm \sqrt{{2}/{T}} \cdot \sin(2\pi f_{\rm T}t )\hspace{0.05cm}.$$
Richtig sind also die Lösungsvorschläge 2 und 3.