Aufgaben:Exercise 4.13: Four-level QAM

• Return to book

Signalraumkonstellation der 4–QAM

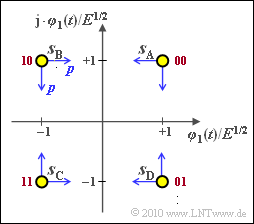
Wir betrachten nun eine Quadraturamplitudenmodulation mit  $M = 4$  Symbolen und den (normierten) Signalraumpunkten

$$\boldsymbol{ s}_{\rm A} = (+1, +1)\hspace{0.05cm},\hspace{0.2cm}\boldsymbol{ s}_{\rm B} = (-1, +1)\hspace{0.05cm},\hspace{0.2cm} \boldsymbol{ s}_{\rm C} = (-1, -1)\hspace{0.05cm},\hspace{0.2cm}\boldsymbol{ s}_{\rm D} = (+1, -1) \hspace{0.05cm}.$$

Die Symbole sind gleichwahrscheinlich. Damit kann man zur Berechnung der mittleren Symbolfehlerwahrscheinlichkeit auf die Mittelung verzichten.

Beispielsweise gilt:

$$p_{\rm S} = {\rm Pr}({\cal{E}}) = {\rm Pr}( \boldsymbol{ s}_{\rm B} \cup \boldsymbol{ s}_{\rm C} \cup \boldsymbol{ s}_{\rm D} \hspace{0.15cm}{\rm entschieden} \hspace{0.05cm}|\hspace{0.05cm} \boldsymbol{ s}_{\rm A}\hspace{0.15cm} {\rm gesendet}) \hspace{0.05cm}.$$

Die Zuordnung der Symbole zu Bitdupeln  kann ebenfalls der Grafik (rote Beschriftungen) entnommen werden. Hierbei ist die Graycodierung vorausgesetzt.

Hinweise:

• Die Aufgabe gehört zum Kapitel  Trägerfrequenzsysteme mit kohärenter Demodulation.
• Bezug genommen eird insbesondere auf die Seite  Quadraturamplitudenmodulation  (QAM).
• Für die Teilaufgabe (4) ist der (zeitdiskrete) AWGN–Kanal mit der Varianz  $\sigma_n^2 = N_0/2$  vorausgesetzt.
• Für die Wahrscheinlichkeit, dass durch das Rauschsignal  $n$  ein Symbol horizontal oder vertikal verfälscht wird, gilt mit der komplementären Gaußschen Fehlerfunktion  $\rm Q(x)$:

$$p = {\rm Pr}( n < -x_0) = {\rm Pr}( n > + x_0) = {\rm Q}(x_0 / \sigma_n) \hspace{0.05cm}.$$

Fragebogen

1

Geben Sie als obere Schranke für die Symbolfehlerwahrscheinlichkeit  $p_{\rm S}$ die „Union Bound” an  $(p_{\rm UB} ≥ p_{\rm S})$. Es gelte  $p = 0.1$.

$p_{\rm UB}\ = \ $

2

Wie groß ist die tatsächliche Symbolfehlerwahrscheinlichkeit  $p_{\rm S}$?

$p_{\rm S}\ = \ $

3

Wie groß ist die Bitfehlerwahrscheinlichkeit bei Graycodierung  $p_{\rm B}$?

$p_{\rm B}\ = \ $

4

Welcher Zusammenhang besteht zwischen  $p_{\rm B}$  und  $E_{\rm B}/N_0$?

	$p_{\rm B} = {\rm Q}\big [\sqrt {E_{\rm B}/N_0}\big ]$,
	$p_{\rm B} = {\rm Q}\big [\sqrt {2E_{\rm B}/N_0}\big ]$,
	$p_{\rm B} = {\rm Q}\big [\sqrt {E_{\rm B}/(2N_0)}\big ]$.

Musterlösung

Solution

(1)  Die „Union Bound” ist eine obere Schranke für die mittlere Symbolfehlerwahrscheinlichkeit. Für letztere gilt:

$$p_{\rm S} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {\rm Pr}({\cal{E}}) = {\rm Pr}( {\cal{E}} \hspace{0.05cm}|\hspace{0.05cm} \boldsymbol{ s}_{\rm A}\hspace{0.15cm} {\rm gesendet})= {\rm Pr}( \boldsymbol{ s}_{\rm B} \cup \boldsymbol{ s}_{\rm C} \cup \boldsymbol{ s}_{\rm D} \hspace{0.15cm}{\rm entschieden} \hspace{0.05cm}|\hspace{0.05cm} \boldsymbol{ s}_{\rm A}\hspace{0.15cm} {\rm gesendet}) \hspace{0.05cm}.$$

• Dagegen gilt für die (verbesserte) „Union Bound” im vorliegenden Beispiel:

$$p_{\rm UB} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {\rm Pr}( \boldsymbol{ s}_{\rm B} \cup \boldsymbol{ s}_{\rm C} \hspace{0.15cm}{\rm entschieden} \hspace{0.05cm}|\hspace{0.05cm} \boldsymbol{ s}_{\rm A}\hspace{0.15cm} {\rm gesendet}) +{\rm Pr}( \boldsymbol{ s}_{\rm C} \cup \boldsymbol{ s}_{\rm D} \hspace{0.15cm}{\rm entschieden} \hspace{0.05cm}|\hspace{0.05cm} \boldsymbol{ s}_{\rm A}\hspace{0.15cm} {\rm gesendet}) = 2p = \underline{0.2} \hspace{0.05cm}.$$

(2)  Die beiden Wahrscheinlichkeiten, aus der sich die „Union Bound” additiv zusammensetzt, lassen sich geometrisch wie folgt deuten:

• ${\rm Pr}(\boldsymbol{s}_{\rm B} \cup \boldsymbol{s}_{\rm C} | \boldsymbol{s}_{\rm A})$ ist die Wahrscheinlichkeit, dass der Empfangspunkt in der linken Halbebene liegt
  ⇒   die AWGN–Rauschkomponente $n_1$ ist negativ und betragsmäßig größer als $\sqrt {E}$.
• ${\rm Pr}(\boldsymbol{s}_{\rm C} \cup \boldsymbol{s}_{\rm D} | \boldsymbol{s}_{\rm A})$ ist die Wahrscheinlichkeit, dass der Empfangspunkt in der unteren Halbebene liegt
  ⇒   die AWGN–Rauschkomponente $n_2$ ist negativ und betragsmäßig größer als $\sqrt {E}$.

Die „Union Bound” berücksichtigt also den dritten Quadranten zweimal. Diesen Fehler kann man hier relativ einfach kompensieren:

$$p_{\rm S} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} p_{\rm UB} - {\rm Pr}( \boldsymbol{ s}_{\rm C} \hspace{0.15cm}{\rm entschieden} \hspace{0.05cm}|\hspace{0.05cm} \boldsymbol{ s}_{\rm A}\hspace{0.15cm} {\rm gesendet}) = 2 p - {\rm Pr}\left [ ( n_1 < -\sqrt{E})\cap ( n_2 < -\sqrt{E})\right ] = 2p - p^2 = \underline{0.19} \hspace{0.05cm}.$$

Hierbei ist berücksichtigt, dass die Rauschkomponenten $n_1$ und $n_2$ voneinander unabhängig sind.

(3)  Wie in der Teilaufgabe (2) nachgewiesen wurde, gelten für die einzelnen Verfälschungswahrscheinlichkeiten:

• Quadrant 2: ${\rm Pr}(\boldsymbol{s}_{\rm B} \ {\rm empfangen} \ | \ \boldsymbol{s}_{\rm A} \ {\rm gesendet}) = 0.09$,
• Quadrant 3: ${\rm Pr}(\boldsymbol{s}_{\rm C} \ {\rm empfangen} \ | \ \boldsymbol{s}_{\rm A} \ {\rm gesendet}) = 0.01$,
• Quadrant 4: ${\rm Pr}(\boldsymbol{s}_{\rm D} \ {\rm empfangen} \ | \ \boldsymbol{s}_{\rm A} \ {\rm gesendet}) = 0.09$.

Für die mittlere Bitfehlerwahrscheinlichkeit erhält man somit:

$$p_{\rm B} = { 1}/{ 2} \cdot \big [ 1 \cdot 0.09 + 2 \cdot 0.01 + 1 \cdot 0.09\big ]= \underline{0.1} = p \hspace{0.05cm}.$$

• Berücksichtigt ist, dass der Quadrant 2 und der Quadrant 4 jeweils nur zu einem Bitfehler führt, der Quadrant 3 dagegen zu zweien.
• Der Faktor $1/2$ berücksichtigt wieder, dass jeweils ein Symbol zwei Binärzeichen (Bit) beinhaltet.

(4)  Die Bitfehlerwahrscheinlichkeit ist nach der Lösung zur Teilaufgabe (2) gleich der Wahrscheinlichkeit, dass die beiden Rauschkomponenten gewisse Grenzen überschreiten:

$$p_{\rm B} = {\rm Pr}( n_1 < -\sqrt{E}) = {\rm Pr}( n_2 < -\sqrt{E}) \hspace{0.05cm}.$$

• Beim AWGN–Kanal lautet diese Wahrscheinlichkeit mit der Varianz $\sigma_n^2 = N_0/2$:

$$p_{\rm B} = {\rm Q} \left ( { { \sqrt{E}}/{ \sigma_n} }\right ) = {\rm Q} \left ( \sqrt{ { {2E}}/{ N_0} }\right ) \hspace{0.05cm}.$$

• Die mittlere Energie pro Symbol kann am einfachsten durch Mittelung über die quadratischen Abstände der Signalraumpunkte vom Ursprung bestimmt werden. Daraus ergibt sich $E_{\rm S} = 2E$.
• Die mittlere Energie pro Bit ist halb so groß: $E_{\rm B} = E_{\rm S}/2 = E$. Daraus folgt:

$$p_{\rm B} = {\rm Q} \left ( \sqrt{ { {2E_{\rm B}}}/{ N_0} }\right ) \hspace{0.05cm}.$$

• Richtig ist also der zweite Lösungsvorschlag.
• Zum gleichen Ergebnis kommt man auch, wenn man die 4–QAM wie im Kapitel Struktur des optimalen Empfängers des Buches „Modulationsverfahren” als zwei orthogonale (das heißt: sich nicht störende) BPSK–Systeme über den gleichen Kanal betrachtet.