Difference between revisions of "Applets:Huffman- und Shannon-Fano-Codierung"
| Line 112: | Line 112: | ||
::$$L_{\mu} = {\rm log}_2\hspace{0.1cm}(1/p_{\mu} ) \hspace{0.05cm}.$$ | ::$$L_{\mu} = {\rm log}_2\hspace{0.1cm}(1/p_{\mu} ) \hspace{0.05cm}.$$ | ||
| + | |||
| + | Da $L_μ$ im Gegensatz zu $\log_2(1/ p_μ$) ganzzahlig ist, gelingt dies nicht immer. | ||
Natürlich gelingt das nicht immer, sondern nur dann, wenn alle Auftrittswahrscheinlichkeiten $p_μ$ in der Form $2^{–k}$ mit $k = 1, 2, 3,$ ... dargestellt werden können. | Natürlich gelingt das nicht immer, sondern nur dann, wenn alle Auftrittswahrscheinlichkeiten $p_μ$ in der Form $2^{–k}$ mit $k = 1, 2, 3,$ ... dargestellt werden können. | ||
| Line 193: | Line 195: | ||
===Der Shannon–Fano–Algorithmus === | ===Der Shannon–Fano–Algorithmus === | ||
| − | + | ||
| + | 1949 – also bereits drei Jahre vor David A. Huffman – haben [https://de.wikipedia.org/wiki/Claude_Shannon Claude E. Shannon] und [https://de.wikipedia.org/wiki/Robert_Fano Robert Fano] einen ähnlichen, auf ''Entropiecodierung'' basierenden Algorithmus angegeben, nämlich: | ||
| + | :# Man ordne die Quellensymbole nach fallenden Auftrittswahrscheinlichkeiten (identisch mit Huffman). | ||
| + | :# Man teile die sortierten Zeichen in zwei möglichst gleichwahrscheinliche Gruppen ein. | ||
| + | :# Der ersten Gruppe wird das Binärsymbol '''1''' zugeordnet, der zweiten die '''0''' (oder umgekehrt). | ||
| + | :# Sind in einer Gruppe mehr als ein Zeichen, so ist auf diese der Algorithmus rekursiv anzuwenden. | ||
| + | |||
| + | {{GraueBox|TEXT= | ||
| + | $\text{Beispiel 4:}$ Wir gehen wie im [[Informationstheorie/Entropiecodierung_nach_Huffman#Der_Huffman.E2.80.93Algorithmus|Einführungsbeispiel für den Huffman–Algorithmus]] zu Beginn des letzten Kapitels von $M = 6$ Symbolen und den folgenden Wahrscheinlichkeiten aus: | ||
| + | |||
| + | :$$p_{\rm A} = 0.30 \hspace{0.05cm},\hspace{0.2cm}p_{\rm B} = 0.24 \hspace{0.05cm},\hspace{0.2cm}p_{\rm C} = 0.20 \hspace{0.05cm},\hspace{0.2cm} | ||
| + | p_{\rm D} = 0.12 \hspace{0.05cm},\hspace{0.2cm}p_{\rm E} = 0.10 \hspace{0.05cm},\hspace{0.2cm}p_{\rm F} = 0.04 | ||
| + | \hspace{0.05cm}.$$ | ||
| + | |||
| + | Dann lautet der Shannon–Fano–Algorithmus: | ||
| + | :# $\rm AB$ → '''1'''x (Wahrscheinlichkeit 0.54), $\rm CDEF$ → '''0'''x (Wahrscheinlichkeit 0.46), | ||
| + | :# $\underline{\rm A}$ → '''<u>11</u>''' (Wahrscheinlichkeit 0.30), $\underline{\rm B}$ ⇒ '''<u>10</u>''' (Wahrscheinlichkeit 0.24), | ||
| + | :# $\underline{\rm C}$ → '''<u>01</u>''' (Wahrscheinlichkeit 0.20), $\rm DEF$ → '''00'''x, (Wahrscheinlichkeit 0.26), | ||
| + | :# $\underline{\rm D}$ → '''<u>001</u>''' (Wahrscheinlichkeit 0.12), $\rm EF$ → '''000'''x (Wahrscheinlichkeit 0.14), | ||
| + | :# $\underline{\rm E}$ → '''<u>0001</u>''' (Wahrscheinlichkeit 0.10), $\underline{\rm F}$ → '''<u>0000</u>''' (Wahrscheinlichkeit 0.04). | ||
| + | |||
| + | ''Anmerkungen'': | ||
| + | *Ein „x” weist wieder darauf hin, dass in nachfolgenden Codierschritten noch Bits hinzugefügt werden müssen. | ||
| + | *Es ergibt sich hier zwar eine andere Zuordnung als bei der [[Informationstheorie/Entropiecodierung_nach_Huffman#Der_Huffman.E2.80.93Algorithmus|Huffman–Codierung]], aber genau die gleiche mittlere Codewortlänge: | ||
| + | |||
| + | :$$L_{\rm M} = (0.30\hspace{-0.05cm}+\hspace{-0.05cm} 0.24\hspace{-0.05cm}+ \hspace{-0.05cm}0.20) \hspace{-0.05cm}\cdot\hspace{-0.05cm} 2 + 0.12\hspace{-0.05cm} \cdot \hspace{-0.05cm} 3 + (0.10\hspace{-0.05cm}+\hspace{-0.05cm}0.04) \hspace{-0.05cm}\cdot \hspace{-0.05cm}4 = 2.4\,{\rm bit/Quellensymbol}\hspace{0.05cm}.$$}} | ||
| + | |||
| + | |||
| + | Mit den Wahrscheinlichkeiten entsprechend dem $\text{Beispiel 1}$ führt der Shannon–Fano–Algorithmus zur gleichen mittleren Codewortlänge wie die Huffman–Codierung. Ebenso sind bei vielen (eigentlich: den meisten) anderen Wahrscheinlichkeitsprofilen Huffman und Shannon–Fano aus informationstheoretischer Sicht äquivalent. | ||
| + | |||
| + | Es gibt aber durchaus Fälle, bei denen sich beide Verfahren hinsichtlich der (mittleren) Codewortlänge unterscheiden, wie das folgende Beispiel zeigt. | ||
| + | |||
| + | {{GraueBox|TEXT= | ||
| + | $\text{Beispiel 2:}$ Wir betrachten $M = 5$ Symbole mit folgenden Wahrscheinlichkeiten: | ||
| + | |||
| + | :$$p_{\rm A} = 0.38 \hspace{0.05cm}, \hspace{0.2cm}p_{\rm B}= 0.18 \hspace{0.05cm}, \hspace{0.2cm}p_{\rm C}= 0.16 \hspace{0.05cm},\hspace{0.2cm} | ||
| + | p_{\rm D}= 0.15 \hspace{0.05cm}, \hspace{0.2cm}p_{\rm E}= 0.13 \hspace{0.3cm} | ||
| + | \Rightarrow\hspace{0.3cm} H = 2.19\,{\rm bit/Quellensymbol} | ||
| + | \hspace{0.05cm}. $$ | ||
| + | |||
| + | [[File:P_ID2461__Inf_T_2_4_S1_ganz_neu.png|center|frame|Baumstrukturen nach Shannon–Fano bzw. Huffman]] | ||
| + | |||
| + | Die Grafik zeigt die jeweiligen Codebäume für Shannon–Fano (links) bzw. Huffman (rechts). Die Ergebnisse lassen sich wie folgt zusammenfassen: | ||
| + | * Der Shannon–Fano–Algorithmus führt zum Code $\rm A$ → '''11''', $\rm B$ → '''10''', $\rm C$ → '''01''', $\rm D$ → '''001''', $\rm E$ → '''000''' und damit zur mittleren Codewortlänge | ||
| + | |||
| + | :$$L_{\rm M} = (0.38 + 0.18 + 0.16) \cdot 2 + (0.15 + 0.13) \cdot 3 = 2.28\,\,{\rm bit/Quellensymbol}\hspace{0.05cm}.$$ | ||
| + | |||
| + | *Mit „Huffman” erhält man $\rm A$ → '''1''', $\rm B$ → '''001''', $\rm C$ → '''010''', $\rm D$ → '''001''', $\rm E$ → '''000''' und eine etwas kleinere mittlere Codewortlänge: | ||
| + | |||
| + | :$$L_{\rm M} = 0.38 \cdot 1 + (1-0.38) \cdot 3 = 2.24\,\,{\rm bit/Quellensymbol}\hspace{0.05cm}. $$ | ||
| + | |||
| + | *Es gibt keinen Satz von Wahrscheinlichkeiten, bei denen Shannon–Fano ein besseres Ergebnis liefert als der Huffman–Algorithmus, der stets den bestmöglichen Entropiecodierer bereitstellt. | ||
| + | *Die Grafik zeigt zudem, dass die Algorithmen im Baumdiagramm in unterschiedlichen Richtungen vorgehen, nämlich einmal von der Wurzel zu den Einzelsymbolen (Shannon–Fano), zum anderen von den Einzelsymbolen zur Wurzel (Huffman).}} | ||
Revision as of 15:09, 6 May 2019
Contents
Programmbeschreibung
Dieses Applet verdeutlicht die Quellencodierverfahren nach Huffman bzw. Shannon–Fano. Diese Verfahren komprimieren redundante wertdiskrete Quellen ohne Gedächtnis mit Stufenzahl $M$, dem Symbolvorrat $\{ \hspace{0.05cm}q_{\mu}\hspace{0.01cm} \} = \{ \rm A, \hspace{0.1cm} B, \hspace{0.1cm}\text{ ...}\}$ und den Symbolwahrscheinlichkeiten $p_{\rm A} \hspace{0.05cm},\hspace{0.1cm} p_{\rm B} \hspace{0.05cm}, \hspace{0.05cm}\text{ ...}$ .
Ziel der Quellencodierung und insbesondere der Klasse der Entropiecodierung – zu der „Huffman” und „Shannon–Fano” gehören – ist, dass die mittlere Codewortlänge $L_{\rm M}$ des binären Codes – darstellbar durch unterschiedlich lange Folgen von Nullen und Einsen – möglichst nahe an die Quellenentropie
- $$H = \sum_{\mu = 1}^{M} \hspace{0.2cm} {\rm Pr}(q_{\mu}) \cdot {\rm log_2}\hspace{0.1cm}\frac {1}{{\rm Pr}(q_{\mu})} = -\sum_{\mu = 1}^{M} \hspace{0.2cm} {\rm Pr}(q_{\mu}) \cdot {\rm log_2}\hspace{0.1cm}{\rm Pr}(q_{\mu})\hspace{0.5cm}\big[\hspace{0.05cm}{\rm Einheit\hspace{-0.1cm}: \hspace{0.1cm}bit/Quellensymbol}\hspace{0.05cm}\big]$$
heranreicht. Allgemein gilt $L_{\rm M} \ge H$, wobei das Gleichheitszeichen nicht für alle Symbolwahrscheinlichkeiten erreicht werden kann.
Dargestellt werden jeweils
- das Baumdiagramm zur Herleitung des jeweiligen Binärcodes, und
- eine simulierte Quellensymbolfolge der Länge $N = 10000$ (Entropie $H\hspace{0.05cm}' \approx H)$ und die dazugehörige Codesymbolfolge der Länge $L_{\rm M}\hspace{0.05cm}' \hspace{-0.03cm}\cdot \hspace{-0.03cm} N$.
Auf die Einheiten „$\rm bit/Quellensymbol$” für die Entropie und die mittlere Codewortlänge wird im Programm verzichtet.
Theoretischer Hintergrund
Der Huffman–Algorithmus
Wir setzen voraus, dass die Quellensymbole $q_\nu$ einem Alphabet $\{q_μ\} = \{$ $\rm A$, $\rm B$ , $\rm C$ , ...$\}$ mit dem Symbolumfang $M$ entstammen und statistisch voneinander unabhängig seien. Beispielsweise gelte für den Symbolumfang $M = 8$:
- $$\{ \hspace{0.05cm}q_{\mu} \} = \{ \boldsymbol{\rm A} \hspace{0.05cm}, \boldsymbol{\rm B}\hspace{0.05cm}, \boldsymbol{\rm C}\hspace{0.05cm}, \boldsymbol{\rm D}\hspace{0.05cm}, \boldsymbol{\rm E}\hspace{0.05cm}, \boldsymbol{\rm F}\hspace{0.05cm}, \boldsymbol{\rm G}\hspace{0.05cm}, \boldsymbol{\rm H}\hspace{0.05cm} \}\hspace{0.05cm}.$$
David A. Huffman hat 1952 – also kurz nach Shannons bahnbrechenden Veröffentlichungen zur Informationstheorie – einen Algorithmus zur Konstruktion von optimalen präfixfreien Codes angegeben. Dieser Huffman–Algorithmus soll ohne Herleitung und Beweis angegeben werden, wobei wir uns hier auf Binärcodes beschränken. Das heißt: Für die Codesymbole gelte stets $c_ν ∈ \{$0, 1$\}$. Hier ist die Vorgehensweise:
- Man ordne die Symbole nach fallenden Auftrittswahrscheinlichkeiten.
- Man fasse die zwei unwahrscheinlichsten Symbole zu einem neuen Symbol zusammen.
- Man wiederhole (1) und (2), bis nur mehr zwei (zusammengefasste) Symbole übrig bleiben.
- Man codiert die wahrscheinlichere Symbolmenge mit 1 und die andere Menge mit 0.
- Man ergänzt in Gegenrichtung (also von unten nach oben) die jeweiligen Binärcodes der aufgespaltenen Teilmengen gemäß den Wahrscheinlichkeiten mit 1 bzw. 0.
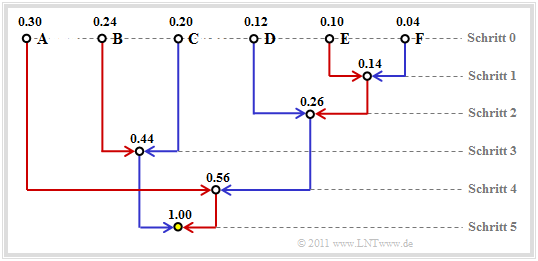
$\text{Beispiel 1:}$ Ohne Einschränkung der Allgemeingültigkeit setzen wir voraus, dass die $M = 6$ Symbole $\rm A$, ... , $\rm F$ schon nach ihren Wahrscheinlichkeiten geordnet sind:
- $$p_{\rm A} = 0.30 \hspace{0.05cm},\hspace{0.2cm}p_{\rm B} = 0.24 \hspace{0.05cm},\hspace{0.2cm}p_{\rm C} = 0.20 \hspace{0.05cm},\hspace{0.2cm} p_{\rm D} = 0.12 \hspace{0.05cm},\hspace{0.2cm}p_{\rm E} = 0.10 \hspace{0.05cm},\hspace{0.2cm}p_{\rm F} = 0.04 \hspace{0.05cm}.$$
Durch paarweises Zusammenfassen und anschießendem Sortieren erhält man in fünf Schritten die folgenden Symbolkombinationen
(resultierende Wahrscheinlichkeiten in Klammern):
- 1. $\rm A$ (0.30), $\rm B$ (0.24), $\rm C$ (0.20), $\rm EF$ (0.14), $\rm D$ (0.12),
- 2. $\rm A$ (0.30), $\rm EFD$ (0.26), $\rm B$ (0.24), $\rm C$ (0.20),
- 3. $\rm BC$ (0.44), $\rm A$ (0.30), $\rm EFD$ (0.26),
- 4. $\rm AEFD$ (0.56), $\rm BC$ (0.44),
- 5. Root $\rm AEFDBC$ (1.00).
Rückwärts – alsogemäß den Schritten (5) bis (1) – erfolgt dann die Zuordnung zu Binärsymbolen. Ein x weist darauf hin, dass in den nächsten Schritten noch Bits hinzugefügt werden müssen:
- 5. $\rm AEFD$ → 1x, $\rm BC$ → 0x,
- 4. $\underline{\rm A}$ → 11, $\rm EFD$ → 10x,
- 3. $\underline{\rm B}$ → 01, $\underline{\rm C}$ → 00,
- 2. $\rm EF$ → 101x, $\underline{\rm D}$ → 100,
- 1. $\underline{\rm E}$ → 1011, $\underline{\rm F}$ → 1010.
Die Unterstreichungen markieren die endgültige Binärcodierung.
Zum Begriff „Entropiecodierung”
Wir gehen weiterhin von den Wahrscheinlichkeiten und Zuordnungen des letzten Beispiels aus:
- $$p_{\rm A} = 0.30 \hspace{0.05cm},\hspace{0.2cm}p_{\rm B} = 0.24 \hspace{0.05cm},\hspace{0.2cm}p_{\rm C} = 0.20 \hspace{0.05cm},\hspace{0.2cm} p_{\rm D} = 0.12 \hspace{0.05cm},\hspace{0.2cm}p_{\rm E} = 0.10 \hspace{0.05cm},\hspace{0.2cm}p_{\rm F} = 0.04 \hspace{0.05cm};$$
- $$\boldsymbol{\rm A} \hspace{0.05cm} \rightarrow \hspace{0.05cm} \boldsymbol{\rm 11} \hspace{0.05cm},\hspace{0.2cm} \boldsymbol{\rm B} \hspace{0.05cm} \rightarrow \hspace{0.05cm} \boldsymbol{\rm 01} \hspace{0.05cm},\hspace{0.2cm} \boldsymbol{\rm C} \hspace{0.05cm} \rightarrow \hspace{0.05cm} \boldsymbol{\rm 00} \hspace{0.05cm},\hspace{0.2cm} \boldsymbol{\rm D} \hspace{0.05cm} \rightarrow \hspace{0.05cm} \boldsymbol{\rm 100} \hspace{0.05cm},\hspace{0.2cm} \boldsymbol{\rm E} \hspace{0.05cm} \rightarrow \hspace{0.05cm} \boldsymbol{\rm 1011} \hspace{0.05cm},\hspace{0.2cm} \boldsymbol{\rm F} \hspace{0.05cm} \rightarrow \hspace{0.05cm} \boldsymbol{\rm 1010} \hspace{0.05cm}.$$
Von den sechs Quellensymbolen werden also drei mit je zwei Bit, eines mit drei Bit und zwei Symbole $(\rm E$ und $\rm F)$ mit vier Bit codiert.
Die mittlere Codewortlänge ergibt sich damit zu
- $$L_{\rm M} = (0.30 \hspace{-0.05cm}+ \hspace{-0.05cm}0.24 \hspace{-0.05cm}+ \hspace{-0.05cm} 0.20) \cdot 2 + 0.12 \cdot 3 + (0.10 \hspace{-0.05cm}+ \hspace{-0.05cm} 0.04 ) \cdot 4 = 2.4 \,{\rm bit/Quellensymbol} \hspace{0.05cm}.$$
Aus dem Vergleich mit der Quellenentropie
- $$H = -\big [0.3 \cdot {\rm log_2}\hspace{0.1cm}(0.3) + 0.24 \cdot {\rm log_2}\hspace{0.1cm}(0.24) + 0.2 \cdot {\rm log_2}\hspace{0.1cm}(0.2)+ 0.12 \cdot {\rm log_2}\hspace{0.1cm}(0.12) + 0.1 \cdot {\rm log_2}\hspace{0.1cm}(0.1)+ 0.04 \cdot {\rm log_2}\hspace{0.1cm}(0.04) \big ]= 2.365 \ \rm bit/Quellensymbol$$
erkennt man die Effizienz der Huffman–Codierung.
$\text{Beispiel 2:}$ Wären die Symbolwahrscheinlichkeiten
- $$p_{\rm A} = p_{\rm B} = p_{\rm C} = 1/4 \hspace{0.05cm},\hspace{0.2cm} p_{\rm D} = 1/8 \hspace{0.05cm},\hspace{0.2cm}p_{\rm E} = p_{\rm F} = 1/16 \hspace{0.05cm},$$
so würde für die Entropie und für die mittlere Codewortlänge gleichermaßen gelten:
- $$H = 3 \cdot 1/4 \cdot {\rm log_2}\hspace{0.1cm}(4) + 1/8 \cdot {\rm log_2}\hspace{0.1cm}(8) + 2 \cdot 1/16 \cdot {\rm log_2}\hspace{0.1cm}(16) = 2.375 \,{\rm bit/Quellensymbol}\hspace{0.05cm},$$
- $$L_{\rm M} = 3 \cdot 1/4 \cdot 2 + 1/8 \cdot 3 + 2 \cdot 1/16 \cdot 4 = 2.375 \,{\rm bit/Quellensymbol} \hspace{0.05cm}.$$
Aus dieser Eigenschaft $L_{\rm M} = H +\varepsilon$ mit $\varepsilon = 0$ bei geeigneten Auftrittswahrscheinlichkeiten erklärt sich der Begriff Entropiecodierung:
- Man versucht bei dieser Form von Quellencodierung, die Länge $L_μ$ der Binärfolge (bestehend aus Nullen und Einsen) für das Symbol $q_μ$ gemäß der Entropieberechnung wie folgt an dessen Auftrittswahrscheinlichkeit $p_μ$ anzupassen:
- $$L_{\mu} = {\rm log}_2\hspace{0.1cm}(1/p_{\mu} ) \hspace{0.05cm}.$$
Da $L_μ$ im Gegensatz zu $\log_2(1/ p_μ$) ganzzahlig ist, gelingt dies nicht immer.
Natürlich gelingt das nicht immer, sondern nur dann, wenn alle Auftrittswahrscheinlichkeiten $p_μ$ in der Form $2^{–k}$ mit $k = 1, 2, 3,$ ... dargestellt werden können.
- In diesem Sonderfall – und nur in diesem – stimmt die mittlere Codewortlänge $L_{\rm M}$ exakt mit der Quellenentropie $H$ überein $(\varepsilon = 0$, siehe $\text{Beispiel 2}$).
- Nach dem Quellencodierungstheorem gibt es keinen (decodierbaren) Code, der im Mittel mit weniger Binärzeichen pro Quellensymbol auskommt.
$\text{Merke:}$ Es gibt keinen präfixfreien (⇒ sofort decodierbaren) Code, der allein unter Ausnutzung der Auftrittswahrscheinlichkeiten zu einer kleineren mittleren Codewortlänge $L_{\rm M}$ führt als der Huffman–Code. In diesem Sinne ist der Huffman–Code optimal.
Darstellung des Huffman–Codes als Baumdiagramm
Häufig wird zur Konstruktion des Huffman–Codes eine Baumstruktur verwendet. Für das bisher betrachtete Beispiel zeigt diese die folgende Grafik:
Man erkennt:
- Bei jedem Schritt des Huffman–Algorithmus werden die beiden Zweige mit den jeweils kleinsten Wahrscheinlichkeiten zusammengefasst.
- Der Knoten im ersten Schritt fasst die zwei Symbole $\rm E$ und $\rm F$ mit den aktuell kleinsten Wahrscheinlichkeiten zusammen. Dieser Knoten ist mit $p_{\rm E} + p_{\rm F} = 0.14$ beschriftet.
- Der vom Symbol mit der kleineren Wahrscheinlichkeit $($hier $\rm F)$ zum Summenknoten verlaufende Zweig ist blau eingezeichnet, der andere Zweig $($für $\rm E)$ rot.
Nach fünf Schritten ist man bei der Baumwurzel („Root”) mit der Gesamtwahrscheinlichkeit $1.00$ angelangt.
Verfolgt man nun den Verlauf von der Wurzel (in obiger Grafik mit gelber Füllung) zu den einzelnen Symbolen zurück, so kann man aus den Farben der einzelnen Zweige die Symbolzuordnung ablesen. Mit den Zuordnungen „rot” → 1 und „blau” → 0 ergibt sich beispielsweise von der Wurzel zu Symbol
- $\rm A$: rot, rot → 11,
- $\rm B$: blau, rot → 01,
- $\rm C$: blau, blau → 00,
- $\rm D$: rot, blau, blau → 100,
- $\rm E$: rot, blau, rot, rot → 1011,
- $\rm F$: rot, blau, rot, blau → 1010.
Die (einheitliche) Zuordnung „rot” → 0 und „blau” → 1 würde ebenfalls zu einem optimalen präfixfreien Huffman–Code führen.
$\text{Beispiel 3:}$ Die folgende Grafik zeigt die Huffman–Codierung von $49$ Symbolen $q_ν ∈ \{$ $\rm A$, $\rm B$, $\rm C$, $\rm D$, $\rm E$, $\rm F$ $\}$ mit der im letzten Abschnitt hergeleiteten Zuordnung. Die binäre Codesymbolfolge weist die mittlere Codewortlänge $L_{\rm M}\hspace{0.05cm}' = 125/49 = 2.551$ auf. Die Farben dienen ausschließlich zur besseren Orientierung.
Aufgrund der kurzen Quellensymbolfolge $(N = 49)$ weichen die Auftrittshäufigkeiten $h_{\rm A}$, ... , $h_{\rm F}$ der simulierten Folgen signifikant von den vorgegebenen Wahrscheinlichkeiten $p_{\rm A}$, ... , $p_{\rm F}$ ab:
- $$p_{\rm A} = 0.30 \hspace{0.05cm} \Rightarrow \hspace{0.05cm} h_{\rm A} = 16/49 \approx 0.326 \hspace{0.05cm},\hspace{0.4cm}p_{\rm B} = 0.24 \hspace{0.05cm} \Rightarrow \hspace{0.05cm} h_{\rm B} = 7/49 \approx 0.143 \hspace{0.05cm},$$
- $$p_{\rm C} =0.24 \hspace{0.05cm} \Rightarrow \hspace{0.05cm} h_{\rm C}= 9/49 \approx 0.184 \hspace{0.05cm},\hspace{0.6cm}p_{\rm D} = 0.12 \hspace{0.05cm} \Rightarrow \hspace{0.05cm} h_{\rm D} = 7/49 \approx 0.143 \hspace{0.05cm},$$
- $$p_{\rm E}=0.10 \hspace{0.05cm} \Rightarrow \hspace{0.05cm} h_{\rm E} = 5/49 \approx 0.102 \hspace{0.05cm},\hspace{0.6cm}p_{\rm F} = 0.04 \hspace{0.05cm} \Rightarrow \hspace{0.05cm} h_{\rm E} = 5/49 \approx 0.102 \hspace{0.05cm}.$$
Damit ergibt sich ein etwas größerer Entropiewert:
- $$H \ ({\rm bez\ddot{u}glich }\hspace{0.15cm}p_{\mu}) = 2.365 \,{\rm bit/Quellensymbol}\hspace{0.3cm} \Rightarrow \hspace{0.3cm} H\hspace{0.05cm}' \ ({\rm bez\ddot{u}glich }\hspace{0.15cm}h_{\mu}) = 2.451 \,{\rm bit/Quellensymbol} \hspace{0.05cm}.$$
Würde man den Huffman–Code mit diesen „neuen” Wahrscheinlichkeiten $h_{\rm A}$, ... , $h_{\rm F}$ bilden, so ergäben sich folgende Zuordnungen:
- $\boldsymbol{\rm A} \hspace{0.05cm} \rightarrow \hspace{0.05cm}$11$\hspace{0.05cm},\hspace{0.2cm} \boldsymbol{\rm B} \hspace{0.05cm} \rightarrow \hspace{0.05cm}$100$\hspace{0.05cm},\hspace{0.2cm} \boldsymbol{\rm C} \hspace{0.05cm} \rightarrow \hspace{0.05cm}$00$\hspace{0.05cm},\hspace{0.2cm} \boldsymbol{\rm D} \hspace{0.05cm} \rightarrow \hspace{0.05cm}$101$\hspace{0.05cm},\hspace{0.2cm} \boldsymbol{\rm E} \hspace{0.05cm} \rightarrow \hspace{0.05cm}$010$\hspace{0.05cm},\hspace{0.2cm} \boldsymbol{\rm F} \hspace{0.05cm} \rightarrow \hspace{0.05cm}$011$\hspace{0.05cm}.$
Nun würden nur $\rm A$ und $\rm C$ mit zwei Bit dargestellt, die anderen vier Symbole durch jeweils drei Bit.
- Die Codesymbolfolge hätte dann eine Länge von $(16 + 9) · 2 + (7 + 7 + 5 + 5) · 3 = 122$ Bit, wäre also um drei Bit kürzer als nach der bisherigen Codierung.
- Die mittlere Codewortlänge wäre dann $L_{\rm M}\hspace{0.05cm}' = 122/49 ≈ 2.49 \ \rm bit/Quellensymbol$ anstelle von $L_{\rm M}\hspace{0.05cm}'≈ 2.55 \ \rm bit/Quellensymbol$.
$\text{Fazit:}$ Dieses Beispiel lässt sich wie folgt interpretieren:
- Die Huffman–Codierung lebt von der (genauen) Kenntnis der Symbolwahrscheinlichkeiten. Sind diese sowohl dem Sender als auch dem Empfänger bekannt, so ist die mittlere Codewortlänge $L_{\rm M}$ oft nur unwesentlich größer als die Quellenentropie $H$.
- Insbesondere aber bei kleinen Dateien kann es zu Abweichungen zwischen den (erwarteten) Symbolwahrscheinlichkeiten $p_μ$ und den (tatsächlichen) Häufigkeiten $h_μ$ kommen. Besser wäre es hier, für jede Datei einen eigenen Huffman–Code zu generieren, der auf den tatsächlichen Gegebenheiten $(h_μ)$ basiert.
- In diesem Fall muss aber dem Decoder auch der spezifische Huffman–Code mitgeteilt werden. Dies führt zu einem gewissen Overhead, der nur wieder bei längeren Dateien vernachlässigt werden kann. Bei kleinen Dateien lohnt sich dieser Aufwand nicht.
Der Shannon–Fano–Algorithmus
1949 – also bereits drei Jahre vor David A. Huffman – haben Claude E. Shannon und Robert Fano einen ähnlichen, auf Entropiecodierung basierenden Algorithmus angegeben, nämlich:
- Man ordne die Quellensymbole nach fallenden Auftrittswahrscheinlichkeiten (identisch mit Huffman).
- Man teile die sortierten Zeichen in zwei möglichst gleichwahrscheinliche Gruppen ein.
- Der ersten Gruppe wird das Binärsymbol 1 zugeordnet, der zweiten die 0 (oder umgekehrt).
- Sind in einer Gruppe mehr als ein Zeichen, so ist auf diese der Algorithmus rekursiv anzuwenden.
$\text{Beispiel 4:}$ Wir gehen wie im Einführungsbeispiel für den Huffman–Algorithmus zu Beginn des letzten Kapitels von $M = 6$ Symbolen und den folgenden Wahrscheinlichkeiten aus:
- $$p_{\rm A} = 0.30 \hspace{0.05cm},\hspace{0.2cm}p_{\rm B} = 0.24 \hspace{0.05cm},\hspace{0.2cm}p_{\rm C} = 0.20 \hspace{0.05cm},\hspace{0.2cm} p_{\rm D} = 0.12 \hspace{0.05cm},\hspace{0.2cm}p_{\rm E} = 0.10 \hspace{0.05cm},\hspace{0.2cm}p_{\rm F} = 0.04 \hspace{0.05cm}.$$
Dann lautet der Shannon–Fano–Algorithmus:
- $\rm AB$ → 1x (Wahrscheinlichkeit 0.54), $\rm CDEF$ → 0x (Wahrscheinlichkeit 0.46),
- $\underline{\rm A}$ → 11 (Wahrscheinlichkeit 0.30), $\underline{\rm B}$ ⇒ 10 (Wahrscheinlichkeit 0.24),
- $\underline{\rm C}$ → 01 (Wahrscheinlichkeit 0.20), $\rm DEF$ → 00x, (Wahrscheinlichkeit 0.26),
- $\underline{\rm D}$ → 001 (Wahrscheinlichkeit 0.12), $\rm EF$ → 000x (Wahrscheinlichkeit 0.14),
- $\underline{\rm E}$ → 0001 (Wahrscheinlichkeit 0.10), $\underline{\rm F}$ → 0000 (Wahrscheinlichkeit 0.04).
Anmerkungen:
- Ein „x” weist wieder darauf hin, dass in nachfolgenden Codierschritten noch Bits hinzugefügt werden müssen.
- Es ergibt sich hier zwar eine andere Zuordnung als bei der Huffman–Codierung, aber genau die gleiche mittlere Codewortlänge:
- $$L_{\rm M} = (0.30\hspace{-0.05cm}+\hspace{-0.05cm} 0.24\hspace{-0.05cm}+ \hspace{-0.05cm}0.20) \hspace{-0.05cm}\cdot\hspace{-0.05cm} 2 + 0.12\hspace{-0.05cm} \cdot \hspace{-0.05cm} 3 + (0.10\hspace{-0.05cm}+\hspace{-0.05cm}0.04) \hspace{-0.05cm}\cdot \hspace{-0.05cm}4 = 2.4\,{\rm bit/Quellensymbol}\hspace{0.05cm}.$$
Mit den Wahrscheinlichkeiten entsprechend dem $\text{Beispiel 1}$ führt der Shannon–Fano–Algorithmus zur gleichen mittleren Codewortlänge wie die Huffman–Codierung. Ebenso sind bei vielen (eigentlich: den meisten) anderen Wahrscheinlichkeitsprofilen Huffman und Shannon–Fano aus informationstheoretischer Sicht äquivalent.
Es gibt aber durchaus Fälle, bei denen sich beide Verfahren hinsichtlich der (mittleren) Codewortlänge unterscheiden, wie das folgende Beispiel zeigt.
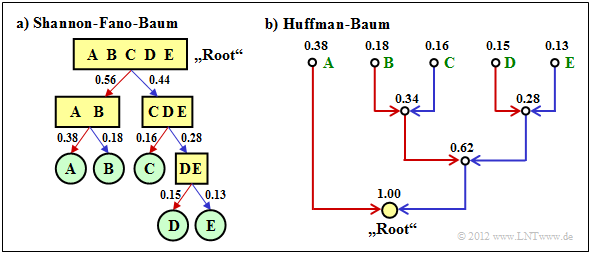
$\text{Beispiel 2:}$ Wir betrachten $M = 5$ Symbole mit folgenden Wahrscheinlichkeiten:
- $$p_{\rm A} = 0.38 \hspace{0.05cm}, \hspace{0.2cm}p_{\rm B}= 0.18 \hspace{0.05cm}, \hspace{0.2cm}p_{\rm C}= 0.16 \hspace{0.05cm},\hspace{0.2cm} p_{\rm D}= 0.15 \hspace{0.05cm}, \hspace{0.2cm}p_{\rm E}= 0.13 \hspace{0.3cm} \Rightarrow\hspace{0.3cm} H = 2.19\,{\rm bit/Quellensymbol} \hspace{0.05cm}. $$
Die Grafik zeigt die jeweiligen Codebäume für Shannon–Fano (links) bzw. Huffman (rechts). Die Ergebnisse lassen sich wie folgt zusammenfassen:
- Der Shannon–Fano–Algorithmus führt zum Code $\rm A$ → 11, $\rm B$ → 10, $\rm C$ → 01, $\rm D$ → 001, $\rm E$ → 000 und damit zur mittleren Codewortlänge
- $$L_{\rm M} = (0.38 + 0.18 + 0.16) \cdot 2 + (0.15 + 0.13) \cdot 3 = 2.28\,\,{\rm bit/Quellensymbol}\hspace{0.05cm}.$$
- Mit „Huffman” erhält man $\rm A$ → 1, $\rm B$ → 001, $\rm C$ → 010, $\rm D$ → 001, $\rm E$ → 000 und eine etwas kleinere mittlere Codewortlänge:
- $$L_{\rm M} = 0.38 \cdot 1 + (1-0.38) \cdot 3 = 2.24\,\,{\rm bit/Quellensymbol}\hspace{0.05cm}. $$
- Es gibt keinen Satz von Wahrscheinlichkeiten, bei denen Shannon–Fano ein besseres Ergebnis liefert als der Huffman–Algorithmus, der stets den bestmöglichen Entropiecodierer bereitstellt.
- Die Grafik zeigt zudem, dass die Algorithmen im Baumdiagramm in unterschiedlichen Richtungen vorgehen, nämlich einmal von der Wurzel zu den Einzelsymbolen (Shannon–Fano), zum anderen von den Einzelsymbolen zur Wurzel (Huffman).
Zusammenfassung und Schlussfolgerungen
Unbekannte Binärquelle
- Ist von der Nachrichtenquelle nicht mehr bekannt als der Symbolunfang $M=2$, so müssen die Entropienäherungen $\hat H_k$ numerisch aus der Quellensymbolfolge $〈 q_1, \hspace{0.05cm} q_2,\hspace{0.05cm}\text{ ...} \hspace{0.05cm}, q_{ν–1}, \hspace{0.05cm}q_ν, \hspace{0.05cm}\hspace{0.05cm}q_{ν+1} ,\hspace{0.05cm}\text{ ...}\hspace{0.05cm},\hspace{0.05cm}q_{N} \hspace{0.05cm}〉$ ermittelt werden. Die Entropie $H$ ergibt sich als der Grenzwert der $\hat H_k$ für $k \to \infty$, wobei gilt:
- $$ H <\text{...} <\hat H_k <\text{...} < \hat H_3 < \hat H_2 < \hat H_1 \le H_0 \hspace{0.05cm}.$$
- Bei der numerischen Ermittlung werden alle Wahrscheinlichkeiten $(p_{\rm A}, \text{...})$ und bedingten Wahrscheinlichkeiten $(p_{\rm A|B}, \text{...})$ durch entsprechende relative Häufigkeiten $(h_{\rm A}, \text{...})$ und bedingte Wahrscheinlichkeiten $(h_{\rm A|B}, \text{...})$ angenähert.
- Die Genauigkeit der numerischen Ermittlung nimmt bei gleichem $N$ mit steigendem $k$ ab. Das heißt: Die Folgenlänge $N$ der Simulation muss an den größten $k$–Wert angepasst werden.
Gedächtnislose Binärquelle
- Eine gedächtnislose Binärquelle ist vollständig durch die Symbolwahrscheinlichkeiten $p_{\rm A}$ und $p_{\rm B} = 1- p_{\rm A}$ charakterisiert. Für die Entropie gilt folgende Gleichung:
- $$H = p \cdot {\rm log_2}\hspace{0.1cm}\frac{1}{\hspace{0.1cm}p\hspace{0.1cm}} + (1-p) \cdot {\rm log_2}\hspace{0.1cm}\frac{1}{1-p} \hspace{0.5cm}{\rm (Einheit\hspace{-0.15cm}: \hspace{0.15cm}bit\hspace{0.15cm}oder\hspace{0.15cm}bit/Symbol)} \hspace{0.05cm}.$$
- Der Maximalwert der Entropie ergibt sich für $p_{\rm A}= p_{\rm B} =0.5$; $H_0 = \log_2 \ M$ bezeichnet man als den Entscheidungsgehalt der Quelle. Im binären Fall $(M = 2)$ gilt:
- $$H_{\rm max} = H_0 = \text{ 1 bit/Symbol}\hspace{0.05cm}.$$
- In diesem Fall $(p_{\rm A}= p_{\rm B} =0.5)$ ist die Symbolfolge redundanzfrei ⇒ die relative Redundanz ist gleich $r = (H - H_0)/H_0= 0$.
- Im unsymmetrischen Fall $(p_{\rm A} \ne p_{\rm B})$ ist die relative Redundanz $r > 0$ und für die Entropie gilt mit den Entropienäherung $H_k$:
- $$H = H_1 < H_0, \hspace{0.5cm}H_1 = H_2 = H_3 = \text{...} .$$
- Bei einer gedächtnislosen Quelle sind also alle (analytisch berechneten) Entropienäherungen $H_k$ exakt gleich. Für die durch Simulation aus der Symbolfolge $〈 q_ν〉$ der Länge $N$ gewonnenen Näherungen $\hat H_k$ gilt dieser Zusammenhang bestenfalls näherungsweise
- $$\hat H_1 \approx \hat H_2 \approx \hat H_3 \approx \text{...} .$$
- Als Ergebnis sollte man $H \approx \hat H_1$ verwenden. Bei gegebenem $N$ sind die auf der Zeitmittelung basierenden Fehler für $\hat H_2$ $\hat H_3$, ... deutlich größer. Oder anders ausgedrückt: Um die gleiche statistische Sicherheit für die Ermittlung von $\hat H_{k+1}$ wie bei $\hat H_k$ zu erzielen, muss man $N$ verdoppeln.
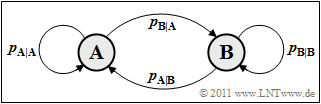
Binäre Markovquelle
- Folgen mit statistischen Bindungen zwischen den Folgenelementen werden oft durch Markovprozesse modelliert, wobei wir uns hier auf binäre Markovprozesse erster Ordnung mit den Symbolen $\rm A$ und $\rm B$ beschränken.
- Für die Entropie $H = H_{\text{M}}$ und die erste Entropienäherung $H_1$ einer solchen Markovquelle gelten die folgenden Gleichungen:
- $$H_{\text{M}} = p_{\rm A} \cdot p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}A} \cdot {\rm log}_2\hspace{0.1cm}\frac {1}{ p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}A}} + p_{\rm A} \cdot p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}A} \cdot {\rm log}_2\hspace{0.1cm}\frac {1}{ p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}A}} + p_{\rm B} \cdot p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}B} \cdot {\rm log}_2\hspace{0.1cm}\frac {1}{ p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}B}} + p_{\rm B} \cdot p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}B} \cdot {\rm log}_2\hspace{0.1cm}\frac {1}{ p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}B}} \hspace{0.05cm},$$
- $$H_1 = p_{\rm A} \cdot (p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}A} + p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}A})\cdot {\rm log}_2\hspace{0.1cm}\frac {1}{p_{\rm A}} + p_{\rm B} \cdot (p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}B} + p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}B})\cdot {\rm log}_2\hspace{0.1cm}\frac {1}{p_{\rm B}} $$
- $$\Rightarrow \hspace{0.3cm}H_1 = p_{\rm A} \cdot {\rm log}_2\hspace{0.1cm}\frac {1}{p_{\rm A}} + p_{\rm B} \cdot {\rm log}_2\hspace{0.1cm}\frac {1}{p_{\rm B}} = H_{\rm bin} (p_{\rm A})= H_{\rm bin} (p_{\rm B}) \hspace{0.05cm}.$$
- Die Entropienäherungen $H_k$ für $k$–Tupel hängen mit der ersten Näherung $H_1$ und dem Endwert $H = H_{\text{M}}$ wie folgt zusammen:
- $$H_k = {1}/{k} \cdot \big [ H_{\rm 1} + (k-1) \cdot H_{\rm M}\big ] \hspace{0.3cm} \Rightarrow \hspace{0.3cm} H_2 = {1}/{2} \cdot \big [ H_{\rm 1} + H_{\rm M} \big ]\hspace{0.05cm}, \hspace{0.3cm} H_3 ={1}/{3} \cdot \big [ H_{\rm 1} + 2 \cdot H_{\rm M}\big ] \hspace{0.05cm},\hspace{0.3cm} H_4 = {1}/{4} \cdot \big [ H_{\rm 1} + 3 \cdot H_{\rm M}\big ] \hspace{0.05cm},\hspace{0.15cm}{\rm usw.}$$
- Daraus folgt direkt: Ist über die Nachrichtenquelle nicht mehr bekannt, als dass es sich um eine Markovquelle erster Ordnung handelt, so kann der Endwert $H = H_{\rm M}$ allein aus den Entropienäherungen $H_1$ und $H_2$ ermittelt werden:
- $$H = 2 \cdot H_2 - H_{\rm 1} \hspace{0.05cm}.$$
Bei einem symmetrischen Markovprozess ⇒ Übergangswahrscheinlichkeiten $p_{\rm {A\hspace{0.01cm}\vert\hspace{0.01cm}B} } = p_{\rm {B\hspace{0.01cm}\vert\hspace{0.01cm}A} } $ ⇒ Symbolwahrscheinlichkeiten $p_{\rm A } = p_{\rm B } = 0.5 $ erhält man
- $$H_{\text{M} } = H_{\text{bin} }(p_{\rm {A\hspace{0.01cm}\vert\hspace{0.01cm}B} })= p_{\rm {A\hspace{0.01cm}\vert\hspace{0.01cm}B} } \cdot {\rm log_2}\hspace{0.1cm}\frac{1}{p_{\rm {A\hspace{0.01cm}\vert\hspace{0.01cm}B} } } + (1 - p_{\rm {A\hspace{0.01cm}\vert\hspace{0.01cm}B} }) \cdot {\rm log_2}\hspace{0.1cm}\frac{1}{1 - p_{\rm {A\hspace{0.01cm}\vert\hspace{0.01cm}B} } },\hspace{0.5cm}H_1 = 1\text{ bit/Symbol} .$$
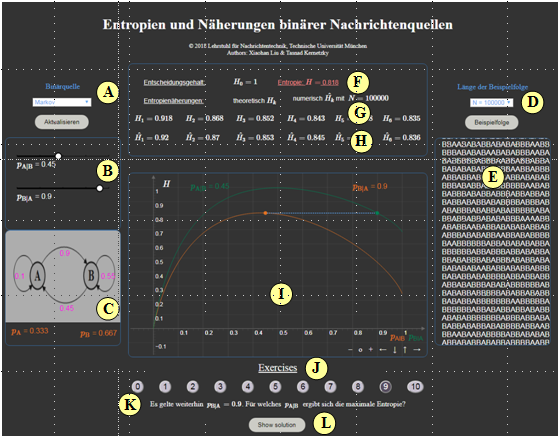
Versuchsdurchführung
- Wählen Sie zunächst die Aufgabennummer.
- Eine Aufgabenbeschreibung wird angezeigt.
- Alle Parameterwerte sind angepasst.
- Alle Entropiewerte werden berechnet und eine Symbolfolge ausgegeben.
- Musterlösung nach Drücken von „Hide solution”.
- Mit der Nummer „0” wird auf die gleichen Einstellung wie beim Programmstart zurückgesetzt.
(1) Wählen Sie die gedächtnislose Binärquelle mit $p_{\rm A} = p_{\rm B} = 0.5$. Wie lauten die analytisch berechneten Entropienäherungen $H_1$, ... , $H_6$?
- Wie unterscheiden sich die Simulationsergebnisse $\hat H_1$, ... , $\hat H_6$ mit $N=10^5$ von $H_1$, ... , $H_6$? Machen Sie jeweils zehn Versuche.
- Es handelt sich um eine redundanzfreie Binärquelle ⇒ $H = H_{\rm bin}(0.5) = H_1 =$ ... $=H_6 = 1\text{ bit/Symbol}$.
- Auch die Simulation mit $N=10^5$ liefert bei (fast) allen Versuchsreihen $\hat H_1 =$ ... $=\hat H_6 = 1.000$ ⇒ das auf drei Nachkommastellen richtige Ergebnis.
(2) Wie unterscheiden sich bei sonst gleichen Einstellungen die Simulationsergebnisse $\hat H_1$, ... , $\hat H_6$ mit $N=10^3$? Wieder jeweils zehn Versuche.
- Die Entropienäherungen $H_k$ werden nun durch $\hat H_k$ ungenauer nachgebildet als mit $N=10^5$ ⇒ die Statistik ist nicht ausreichend.
- Die Simulation mit $N=10^3$ liefert bei zehn Versuchsreihen für $\hat H_1$ entweder $1.000$ oder $0.999$ und für $\hat H_6$ Werte zwischen $0.982$ und $0.995$
- ⇒ Simulationsgenauigkeit nimmt mit steigendem $k$ ab. Die simulierten Werte $\hat H_k$ sind stets kleiner als $H_k = 1.000$. Beides gilt auch für noch kleineres $N$.
(3) Wählen Sie nun die gedächtnislose Binärquelle mit $p_{\rm A} = 0.2$ und $p_{\rm B} = 0.8$. Wie groß sind die Entropie $H$ und die Entropienäherungen $H_1$, ... , $H_6$?
- Wie unterscheiden sich die Simulationsergebnisse $\hat H_1$, ... , $\hat H_6$ mit $N=10^5$ von $H_1$, ... , $H_6$? Wieder jeweils zehn Versuche.
- Es gilt $H = H_{\rm bin}(0.2) = 0.722\text{ bit/Symbol}$. Wie bei jeder gedächtnislosen Nachrichtenquelle gilt auch hier $H_1 =$ ... $=H_6 = H$.
- Die Simulation mit $N=10^5$ liefert bei zehn Versuchsreihen für $\hat H_1$ Werte zwischen $0.719$ und $0.727$. Es gilt aber stets $\hat H_1 =$ ... $= \hat H_6$.
- In solchen Fällen weicht die relative Häufigkeit $h_{\rm A}$ von der Wahrscheinlichkeit $p_{\rm A}$ ab. Ist $\hat H_1 > 0.722$, so ist $h_{\rm A} > 0.2$.
(4) Was ändert sich gegenüber (3) mit den Symbolwahrscheinlichkeiten $p_{\rm A} = 0.8$ und $p_{\rm B} = 0.2$?
- Nichts. Die binäre Entropiefunktion ist symmetrisch um $p=0.5$.
- Ist nun $\hat H_1 > 0.722$, so ist $h_{\rm A} < 0.8$.
(5) Wählen Sie nun die Markovquelle mit $p_{\rm {A\hspace{0.01cm}\vert\hspace{0.01cm}B} } = 0.2$ und $p_{\rm {B\hspace{0.01cm}\vert\hspace{0.01cm}A} } = 0.8$ . Wie groß sind die Entropie $H$ und die Entropienäherungen $H_1$, ... , $H_6$?
- Bei dieser „Markovquelle” ist $p_{\rm {A\hspace{0.01cm}\vert\hspace{0.01cm}B} } = 0.2$ und $p_{\rm {A\hspace{0.01cm}\vert\hspace{0.01cm}A} } = 1 - p_{\rm {B\hspace{0.01cm}\vert\hspace{0.01cm}A} } = 0.2$ . Deshalb ist auch die unbedingte Wahrscheinlichkeit $p_{\rm A} = 0.2$ ⇒ $p_{\rm B} = 0.8$.
- Es handelt sich also um die gleiche gedächtnislose Quelle wie bei (4) ⇒ $H = H_1 =$ ... $=H_6 = 0.722\text{ bit/Symbol}$.
(6) Wählen Sie nun die Markovquelle mit $p_{\rm {A\hspace{0.01cm}\vert\hspace{0.01cm}B} } = 0.2$ und $p_{\rm {B\hspace{0.01cm}\vert\hspace{0.01cm}A} } = 0.2$ . Wie groß sind die Entropie $H$ und die Entropienäherungen $H_1$, ... , $H_6$?
- Hier handelt es sich um eine „echte Markovquelle”, da sich $p_{\rm {A\hspace{0.01cm}\vert\hspace{0.01cm}B} } = 0.2$ und $p_{\rm {A\hspace{0.01cm}\vert\hspace{0.01cm}A} } = 1 - p_{\rm {B\hspace{0.01cm}\vert\hspace{0.01cm}A} } = 0.8$ unterscheiden.
- Wegen $p_{\rm {A\hspace{0.01cm}\vert\hspace{0.01cm}B}} = p_{\rm {B\hspace{0.01cm}\vert\hspace{0.01cm}A}}$ sind die beiden unbedingten Symbolwahrscheinlichkeiten gleich: $p_{\rm A} = p_{\rm B} = 0.5$ ⇒ $H_1 = 1$.
- Die Entropienäherungen $H_k$ werden mit steigendem $k$ kleiner: $H_2 = 0.861$, $H_3 = 0.815$, ... , $H_6 = 0.768$. Der Endwert ist wieder $H = H_\infty = 0.722\text{ bit/Symbol}$.
(7) Welche Unterschiede gegenüber (6) ergeben sich mit $p_{\rm {A\hspace{0.01cm}\vert\hspace{0.01cm}B} } = 0.8$ und $p_{\rm {B\hspace{0.01cm}\vert\hspace{0.01cm}A} } = 0.8$?
- Die Entropienäherung $H = H_{\rm bin}(0.8) = H_{\rm bin}(0.2)= 0.722\text{ bit/Symbol}$ bleibt gleich, ebenso alle Entropienäherungen $H_k$.
- Wegen den größeren Übergangswahrscheinlichkeiten $p_{\rm {A\hspace{0.01cm}\vert\hspace{0.01cm}B}} = p_{\rm {B\hspace{0.01cm}\vert\hspace{0.01cm}A}} = 0.8$ erkennt man jetzt deutlich mehr Übergänge in der ausgegebenen Symbolfolge.
(8) Wählen Sie nun die Markovquelle mit $p_{\rm {A\hspace{0.01cm}\vert\hspace{0.01cm}B} } = 0.8$ und $p_{\rm {B\hspace{0.01cm}\vert\hspace{0.01cm}A} } = 0.9$. Wie groß sind die Entropie $H$ und die Entropienäherungen $H_1$, ... , $H_6$?
- Wegen $p_{\rm {A\hspace{0.01cm}\vert\hspace{0.01cm}B}} \ne p_{\rm {B\hspace{0.01cm}\vert\hspace{0.01cm}A}}$ sind nun die beiden unbedingten Symbolwahrscheinlichkeiten unterschiedlich: $p_{\rm A} = 0.471$ und $p_{\rm B} = 0.529$ ⇒ $H_1 = 0.998 \ne 1$.
- Die Entropienäherungen $H_k$ werden wieder kontinuierlich kleiner: $H_2 = 0.800$, $H_3 = 0.734$, ... , $H_6 = 0.669$. Endwert: $H = H_\infty = 0.603\text{ bit/Symbol}$.
- Aus der Symbolfolge erkennt man, dass zwei Symbole $\rm A$ ganz selten aufeinanderfolgen.
(9) Es gelte weiterhin $p_{\rm {B\hspace{0.01cm}\vert\hspace{0.01cm}A} } = 0.9$. Für welches $p_{\rm {A\hspace{0.01cm}\vert\hspace{0.01cm}B} }$ ergibt sich die maximale Entropie?
- Anhand der roten Kurve in der Grafik zu (8) lässt sich bereits das Ergebnis $p_{\rm {A\hspace{0.01cm}\vert\hspace{0.01cm}B} }\approx 0.45$ abschätzen.
- Der dazugehörige Entropie–Endwert ist $H = H_\infty = 0.818\text{ bit/Symbol}$.
(10) Wählen Sie nun die Markovquelle mit $p_{\rm {A\hspace{0.01cm}\vert\hspace{0.01cm}B} } = 0.8$ und $p_{\rm {B\hspace{0.01cm}\vert\hspace{0.01cm}A} } = 1.0$. Interpretieren Sie die dargestellten Ergebnisse.
- Die unbedingten Symbolwahrscheinlichkeiten sind $p_{\rm A} = 0.444$ und $p_{\rm B} = 0.556$ ⇒ $H_1 = 0.991 \ne 1$. Der Entropie–Endwert ist $H = H_\infty = 0.401\text{ bit/Symbol}$.
- Aus der Symbolfolge erkennt man, dass das Symbol $\rm A$ im Gegensatz zum Symbol $\rm B$ stets isoliert auftritt.
(11) Wählen Sie nun die Markovquelle mit $p_{\rm {A\hspace{0.01cm}\vert\hspace{0.01cm}B} } = 0.8$ und $p_{\rm {B\hspace{0.01cm}\vert\hspace{0.01cm}A} } = 0$. Interpretieren Sie die dargestellten Ergebnisse.
- Die unbedingten Symbolwahrscheinlichkeiten sind $p_{\rm A} = 1$ und $p_{\rm B} = 0$ ⇒ die Symbolfolge besteht nur aus $\rm A$ ⇒ Entropienäherung $H_1 = 0 $.
- Alle weiteren Entropienäherungen $H_k$ und auch der Entropie–Endwert sind ebenfalls Null.
Zur Handhabung des Applets
(A) Auswahl: Gedächtnislose Quelle / Markovquelle
(B) Parametereingabe per Slider (Beispiel Markovquelle)
(C) Markovdiagramm (falls Markovquelle)
(D) Eingabe der Folgenlänge $N$ zur Berechnung der $\hat H_k$
(E) Ausgabe einer simulierten Symbolfolge
(F) Ausgabe des Entropiewertes $H$
(G) Ausgabe der Entropienäherungen $H_k$
(H) Ausgabe der numerisch ermittelten Entropienäherungen $\hat H_k$
(I) Grafikfeld zur Darstellung der Funktion $H(p_{\rm A})$ bzw. $H(p_{\rm A}|p_{\rm B})$
(J) Bereich für die Versuchsdurchführung: Aufgabenauswahl
(K) Bereich für die Versuchsdurchführung: Aufgabenstellung
(L) Bereich für die Versuchsdurchführung: Musterlösung
Über die Autoren
Dieses interaktive Applet wurde am Lehrstuhl für Nachrichtentechnik der Technischen Universität München konzipiert und realisiert.
- Die erste Version wurde 2011 von Eugen Mehlmann im Rahmen seiner Bachelorarbeit mit „FlashMX–Actionscript” erstellt (Betreuer: Günter Söder).
- 2019 wurde das Programm von Xiaohan Liu (Bachelorarbeit, Betreuer: Tasnád Kernetzky ) auf „HTML5” umgesetzt und neu gestaltet.