Aufgaben:Exercise 3.1Z: Spectrum of the Triangular Pulse

• Return to book

Dreieckimpuls

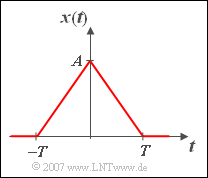
Betrachtet wird ein Dreieckimpuls  ${x(t)}$, der im Bereich  $–T ≤ t ≤ T$  durch folgende Gleichung beschrieben wird:

$$x(t) = A \cdot \left( {1 - {\left| \hspace{0.05cm}t \hspace{0.05cm}\right|}/{T}} \right).$$

Die Impulsamplitude sei  $A = 1\, \text{V}$, der Zeitparameter  $T = 1 \text{ ms}$. Für alle Zeiten  $|\hspace{0.05cm} t \hspace{0.05cm} | > T$  ist  ${x(t)} = 0$.

Zur Berechnung der Spektralfunktion  ${X(f)}$  können Sie folgende Eigenschaften ausnutzen:

• Die Zeitfunktion ist gerade und damit die Spektralfunktion reell:

$$X\left( f \right) = \int_{ - \infty }^{ + \infty } {x(t)} \cdot {\rm e}^{{\rm j}2\pi ft} {\rm d}t = 2 \cdot \int_0^{ \infty } {x(t)} \cdot \cos \left( {2\pi ft} \right){\rm d}t.$$

• Für  $|\hspace{0.05cm} t \hspace{0.05cm} | > T$ besitzt ${x(t)}$  keine Anteile:

$$X\left( f \right) = 2 \cdot \int_0^T {x(t)} \cdot \cos \left( {2\pi ft} \right){\rm d}t.$$

Hinweise:

• Die Aufgabe gehört zum Kapitel  Fouriertransformation und –rücktransformation.
• Weitere Informationen zu dieser Thematik liefert das Lernvideo  Kontinuierliche und diskrete Spektren.

• Zur Lösung dieser Aufgabe können Sie auf die folgenden Formeln zurückgreifen:

$$\int {t \cdot \cos \left( {\omega _0 t} \right)\ {\rm d}t = \frac{{\cos \left( {\omega _0 t} \right)}}{\omega _0 ^2 }} + \frac{{t \cdot \sin \left( {\omega _0 t} \right)}}{\omega _0 }, \hspace{0.5cm} \sin ^2 \left( \alpha \right) = {1}/{2} \cdot \left( {1 - \cos \left( {2\alpha } \right)} \right).$$

Fragebogen

1

Berechnen Sie die Spektralfunktion  ${X(f)}$. Welcher Spektralwert ergibt sich bei der Frequenz  $f = 500 \,\text{Hz}$?

$X(f = 500 \,\text{Hz}) \ = \ $  $\text{mV/Hz}$

2

Geben Sie die Spektralfunktion  ${X(f)}$  unter Verwendung der Spaltfunktion  $\text{si}(x) = \sin(x)/x$  an. Welcher Wert ergibt sich für  $f = 0$?

$X(f = 0) \ = \ $  $\text{mV/Hz}$

3

Bei welcher Frequenz  $f = f_0$  hat das Spektrum  ${X(f)}$  die erste Nullstelle?

$f_0 \ = \ $  $\text{kHz}$

4

Welche der beiden Aussagen sind zutreffend?

	Bei allen Vielfachen von  $f_0$  hat das Spektrum Nullstellen.
	Bei der Frequenz  $f = 1.5 \cdot f_0$  ist die Spektralfunktion negativ.

Musterlösung

Solution

(1)  Unter Ausnutzung der genannten Symmetrieeigenschaften gilt mit der Abkürzung  $\omega = 2\pi f$:

$$X(f) = 2A \cdot \int_0^T {\left( {1 -{t}/{T}} \right)} \cdot \cos \left( {\omega t} \right)\hspace{0.1cm}{\rm d}t.$$

• Dieses Integral setzt sich aus zwei Anteilen zusammen:

$$X_1 (f) = 2A \cdot \int_0^T {\cos } \left( {\omega t} \right)\hspace{0.1cm}{\rm d}t = \frac{2A}{\omega } \cdot \sin \left( {\omega T} \right),$$

$$X_2 (f) = - \frac{2A}{T} \cdot \int_0^T {t \cdot \cos } \left( {\omega t} \right)\hspace{0.1cm}{\rm d}t = - \frac{2A}{T} \cdot \left. {\left[ {\frac{{\cos \left( {\omega t} \right)}}{\omega ^2 } + \frac{{t \cdot \sin \left( {\omega t} \right)}}{\omega }} \right]} \right|_0^T .$$

• Unter Berücksichtigung von oberer und unterer Grenze erhält man:

$$X_2 \left( f \right) = - \frac{2A}{T} \cdot \left[ {\frac{{\cos \left( {\omega T} \right)}}{\omega ^2 } - \frac{1}{\omega ^2 } + \frac{{T \cdot \sin \left( {\omega T} \right)}}{\omega }} \right].$$

• Addiert man die beiden Anteile, so ergibt sich:

$$X(f) = \frac{2A}{\omega ^2 \cdot T}\cdot \big[ {1 - \cos \left( {\omega T} \right)} \big] = \frac{A}{2\pi ^2 f^2 T} \cdot \big[ {1 - \cos \left( {2\pi fT} \right)} \big].$$

• Bei der Frequenz  $f = 1/(2T) = 500 \,\text{Hz}$  ist das Argument der Cosinusfunktion gleich  $\pi$  und die Cosinusfunktion selbst gleich  $-1$. Daraus folgt:

$$X( {f ={1}/{2T} = 500\;{\rm Hz}} ) = \frac{4}{\pi^2} \cdot A \cdot T = \frac{4}{\pi^2} \cdot 1\;{\rm V} \cdot 10^{ - 3}\;{\rm s}\hspace{0.15 cm}\underline{= 0.405 \,{\rm mV/Hz}}.$$

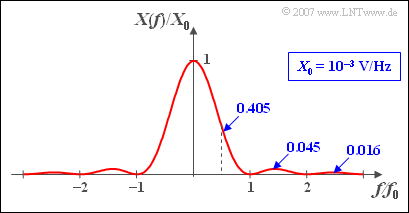
(2)  Mit der trigonometrischen Umformung  ${1}/{2} \cdot (1 - \cos (2 \alpha)) = \sin^2(\alpha)$  erhält man für die Spektralfunktion:

$\rm si$-Quadrat-Spektrum

$$X(f) = A \cdot T \cdot \frac{\sin^2(\pi f T)}{\pi^2 \cdot {f^2 \cdot T^2}} = A \cdot T \cdot {{{\rm si}^2(\pi f T)}}.$$

• Bei der Frequenz  $f = 0$  ist die  $\rm si$-Funktion gleich  $1$. Daraus folgt:

$$X( {f = 0} ) = A \cdot T \hspace{0.15 cm}\underline{= 1\,{\rm mV/Hz}}.$$

(3)  Die erste Nullstelle tritt auf, wenn das Argument der si-Funktion gleich  $\pi$  ist.

• Daraus folgt  $f_0 \cdot T = 1$  bzw.  $f_0 = 1/T \hspace{0.15 cm}\underline{= 1 \ \text{kHz}}$.

(4)  Richtig ist die erste Aussage:

• Das Spektrum  ${X(f)}$  ist bei Vielfachen von  $f_0$  $(f = n \cdot f_0)$  gleich  ${\rm si}^2(n \cdot \pi) = 0$.
• Die zweite Aussage ist falsch:  Bei keiner Frequenz  $f$  ist  ${X(f)} < 0$  (siehe Skizze).