Aufgaben:Exercise 3.7: Synchronous Demodulator

• Return to book

Die Spektralfunktionen  $R(f)$  und  $Z_{\rm E}(f)$

Zur Rücksetzung eines amplitudenmodulierten Signals in den ursprünglichen Frequenzbereich verwendet man oft einen  Synchrondemodulator:

• Dieser multipliziert das AM-Eingangssignal  $r(t)$  mit einem empfangsseitigen Trägersignal  $z_{\rm E}(t)$, das sowohl hinsichtlich Frequenz  $f_{\rm T}$  als auch Phase  $\varphi_{\rm T}$  mit dem sendeseitigen Trägersignal  $z_{\rm S}(t)$  übereinstimmen sollte.
• Es folgt ein rechteckförmiger Tiefpass zur Eliminierung aller spektralen Anteile oberhalb der Trägerfrequenz  $f_{\rm T}$. Das Ausgangssignal des Synchrondemodulators nennen wir  $v(t)$.

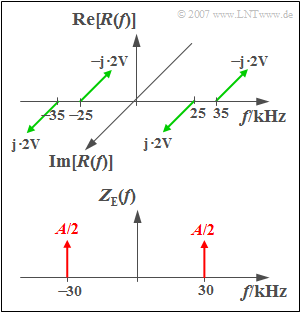
Das oben skizzierte Spektrum  $R(f)$  des Empfangssignals  $r(t)$  ist durch Zweiseitenband–Amplitudenmodulation eines sinusförmigen Quellensignals  $q(t)$  mit der Frequenz  $5\,\text{kHz}$  und der Amplitude  $8\,\text{V}$  entstanden. Als sendeseitiges Trägersignal  $z_{\rm S}(t)$  wurde ein Cosinussignal mit der Frequenz  $30\,\text{kHz}$ verwendet.

Das Spektrum des empfangsseitigen Trägersignals  $z_{\rm E}(t)$  besteht entsprechend der unteren Skizze aus zwei Diraclinien, jeweils mit dem Gewicht  $A/2$. Da  $z_{\rm E}(t)$  keine Einheit beinhalten soll, sind auch die Gewichte der Diracfunktionen dimensionslos.

Hinweise:

• Die Aufgabe gehört zum  Kapitel  Faltungssatz und Faltungsoperation.
• Wichtige Informationen finden Sie vor allem auf der Seite  Faltung einer Funktion mit einer Diracfunktion.

Fragebogen

1

Es gelte  $f_{\rm T} = 30\,\text{kHz}$  und  $A=1$. Berechnen Sie das Ausgangssignal  $v(t)$.
Welcher Signalwert tritt zum Zeitpunkt  $t = 50\, {\rm µ} \text{s}$ auf?

$v(t = 50\, µ\text{s})\ = \ $  $\text{V}$

2

Wie groß muss die Amplitude des empfangsseitigen Trägersignals  $z_{\rm E}(t)$  gewählt werden, damit  $v(t) = q(t)$  gilt?

$A\ = \ $

3

Berechnen Sie das Ausgangssignal  $v(t)$  unter den Voraussetzungen  $A = 2$  und  $f_{\rm T} = 31\,\text{kHz}$.
Welcher Signalwert tritt zum Zeitpunkt  $ t = 50\, µ\text{s}$ auf?

$v(t = 50\, µ\text{s})\ = \ $  $\text{V}$

Musterlösung

Solution

(1)  Benennen wir das Signal nach dem Multiplizierer mit  $m(t) = r(t) \cdot z_{\rm E}(t)$, so ist das zugehörige Spektrum  $M(f)$  das Faltungsprodukt aus  $R(f)$  und  $Z_{\rm E}(f)$.

• Die Faltung des Spektrums  $R(f)$  mit der rechten Diraclinie bei  $+30 \text{ kHz}$  führt zu diskreten Spektrallinien bei  $-\hspace{-0.08cm}5\, \text{kHz}$,  $+5 \,\text{kHz}$,  $+55 \,\text{kHz}$  und  $+65 \,\text{kHz}$. Diese sind alle imaginär und gegenüber den Impulsgewichten von  $R(f)$  um den Faktor  $A/2 = 0.5$  kleiner.
• Die Faltung von  $R(f)$  mit dem Dirac bei  $-\hspace{-0.08cm}30 \,\text{kHz}$  ergibt Linien bei  $-\hspace{-0.08cm}65 \,\text{kHz}$,  $-55 \,\text{kHz}$, $-5 \,\text{kHz}$  und  $+5 \,\text{kHz}$.

Durch Überlagerung der beiden Zwischenresultate und Berücksichtigung des Tiefpassfilters, der die Linien bei  $\pm 55 \text{ kHz}$  und  $\pm 65 \text{ kHz}$  unterdrückt, folgt somit für das Spektrum des Sinkensignals:

$$V( f) = - {\rm{j}} \cdot 2\;{\rm{V}} \cdot \delta ( {f - f_{\rm N} }) + {\rm{j}} \cdot 2\;{\rm{V}} \cdot \delta ( {f + f_{\rm N} } )\hspace{0.3cm}{\rm mit}\hspace{0.3cm}f_{\rm N} = 5\;{\rm kHz}.$$

• Das Sinkensignal  $v(t)$  ist also ein  $5 \text{ kHz}$–Sinussignal mit der Amplitude  $4 \text{ V}$.
• Der Zeitpunkt  $t = 50\, µ\text{s}$  entspricht einem Viertel der Periodendauer  $T_0 = 1/f_{\rm N} = 200\, µ\text{s}$.
• Somit ist hier das Sinkensignal maximal, also  $\underline{4 \text{ V}}$.

(2)  Mit  $A = 1$  ist  $v(t)$  nur halb so groß wie  $q(t)$   ⇒   Mit  $\underline{A = 2}$  wären beide Signale gleich.

(3)  Die Diraclinien bei  $\pm f_{\rm T}$  haben jeweils das Gewicht  $1$. Alle nachfolgend genannten Spektrallinien sind imaginär und betragsmäßig gleich  $2 \text{ V}$.

• Die Faltung von  $R(f)$  mit der rechten Diraclinie von  $z_{\rm E}(t)$  liefert Anteile bei  $-\hspace{-0.08cm}4\, \text{kHz (p: positiv)}$,  $+6 \,\text{kHz (n: negativ)}$, $+56 \,\text{kHz (p)}$  und  $+66 \,\text{kHz (n)}$.
• Dagegen führt die Faltung mit der linken Diracfunktion zu Spektrallinien bei  $-\hspace{-0.08cm}66 \,\text{kHz (p)}$,  $-\hspace{-0.08cm}56 \,\text{kHz (n)}$,  $-\hspace{-0.08cm}6 \,\text{kHz (p)}$  und  $+4 \,\text{kHz (n)}$, alle ebenfalls mit den (betragsmäßigen) Impulsgewichten  $2 \text{ V}$.
• Unter Berücksichtigung des Tiefpasses verbleiben nur die vier Spektrallinien bei  $\pm 4 \,\text{kHz}$  und  $\pm 6 \,\text{kHz}$.
• Das dazugehörige Zeitsignal lautet somit mit  $f_4 = 4 \,\text{kHz}$  und  $f_6 = 6 \,\text{kHz}$:

$$v( t ) = 4\;{\rm{V}} \cdot \sin ( {2{\rm{\pi }}f_4 t} ) + 4\;{\rm{V}} \cdot \sin ( {2{\rm{\pi }}f_6 t} ) \ne q( t ) = 8\;{\rm{V}} \cdot \sin ( {2{\rm{\pi }}f_5 t} ).$$

• Zum Zeitpunkt  $t = 50\, µ\text{s}$  erhält man:

$$v( t = 50\, µ\text{s}) = 4\;{\rm{V}} \cdot \big[ {\sin \big ( {0.4{\rm{\pi }}} ) + \sin ( {0.6{\rm{\pi }}} )} \big]\hspace{0.15 cm}\underline{ = 7.608\;{\rm{V}}}{\rm{.}}$$