Aufgaben:Exercise 3.1: Phase Modulation Locus Curve

• Return to book

Zwei Ortskurven zur Auswahl

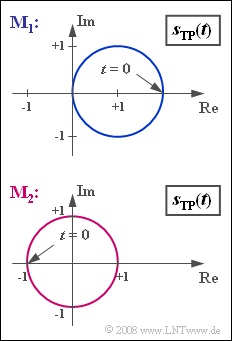
Unter der Ortskurve versteht man allgemein die Darstellung des äquivalenten Tiefpass–Signals  $s_{\rm TP}(t)$  in der komplexen Ebene.

• Die Grafik zeigt Ortskurven am Ausgang zweier Modulatoren  $\rm M_1$  und  $\rm M_2$.
• Real- und Imaginärteil sind in dieser Grafik jeweils auf $1 \ \rm V$ normiert.

Das Quellensignal sei bei beiden Modulatoren gleich:

$$ q(t) = A_{\rm N} \cdot \cos(2 \pi f_{\rm N} \cdot t),\hspace{1cm} {\rm mit}\hspace{0.2cm} A_{\rm N} = 2\,{\rm V},\hspace{0.2cm}f_{\rm N} = 5\,{\rm kHz}\hspace{0.05cm}.$$

Einer der beiden Modulatoren realisiert eine Phasenmodulation, die durch folgende Gleichungen gekennzeichnet ist:

$$ s(t) = A_{\rm T} \cdot \cos \hspace{-0.1cm} \big[\omega_{\rm T} \cdot t + \phi(t) \big]\hspace{0.05cm},$$

$$ s_{\rm TP}(t) = A_{\rm T} \cdot {\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}\phi(t) }\hspace{0.05cm},$$

$$ \phi(t) = K_{\rm PM} \cdot q(t)\hspace{0.05cm}.$$

Den Maximalwert von  $ϕ(t)$  nennt man den  Modulationsindex  $η$.  Oft wird  $η$  in der Literatur auch als  Phasenhub  bezeichnet.

Hinweise:

• Die Aufgabe gehört zum Kapitel  Phasenmodulation.
• Bezug genommen wird insbesondere auf die Seite  Äquivalentes TP-Signal bei Phasenmodulation.

Fragebogen

1

Welches Modulationsverfahren verwendet der Modulator  $\rm M_1$?

	Zweiseitenband–Amplitudenmodulation.
	Einseitenband–Amplitudenmodulation.
	Phasenmodulation.

2

Welches Modulationsverfahren verwendet der Modulator  $\rm M_2$?

	Zweiseitenband–Amplitudenmodulation.
	Einseitenband–Amplitudenmodulation.
	Phasenmodulation.

3

Wie groß ist die Trägeramplitude  $A_{\rm T}$  beim Phasenmodulator?  Beachten Sie die Normierung auf  $1 \ \rm V$.

$A_{\rm T} \ = \ $ $\ \rm V$

4

Welche Werte besitzen der Modulationsindex  $η$  und die Modulatorkonstante  $K_{\rm PM}$?

$η\ = \ $

$K_{\rm PM}\ = \ $ $\ \rm 1/V$

5

Beschreiben Sie die Bewegung auf der Ortskurve.  Zu welcher Zeit  $t_1$  wird erstmals wieder der Ausgangspunkt  $s_{\rm TP}(t = 0) = -1 \ \rm V$  erreicht?

$t_1\ = \ $ $ \ \rm µ s$

Musterlösung

Solution

(1)  Es handelt sich um eine ESB–AM mit dem Seitenband–zu–Träger–Verhältnis $μ = 1$   ⇒   Antwort 2:

• Bewegt man sich auf dem Kreis in mathematisch positive Richtung, so liegt speziell eine OSB–AM vor, andernfalls eine USB–AM.
• Die Phasenfunktion $ϕ(t)$ als der Winkel eines Punktes $s_{\rm TP}(t)$ auf dem Kreis(bogen) bezogen auf den Koordinatenursprung kann Werte zwischen $±π/2$ annehmen und zeigt keinen Cosinusverlauf.
• Aber auch die Hüllkurve $a(t) = |s_{\rm TP}(t)|$ ist nicht cosinusförmig.
• Würde man beim Empfänger für $\rm M_1$ einen Hüllkurvendemodulator einsetzen, so käme es zu nichtlinearen Verzerrungen im Gegensatz zur ZSB–AM, deren Ortskurve eine horizontale Gerade ist.

(2)  Hier handelt es sich um die Phasenmodulation   ⇒   Antwort 3:

• Die Einhüllende $a(t) = A_{\rm T}$ ist konstant, während die Phase $ϕ(t)$ entsprechend dem Quellensignal $q(t)$ cosinusförmig verläuft.

(3)  Bei der Phasenmodulation gilt:

$$s_{\rm TP}(t) = A_{\rm T} \cdot {\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}\phi(t) }\hspace{0.05cm}.$$

Aus der Grafik kann man die Trägeramplitude $A_{\rm T}\hspace{0.15cm}\underline{ = 1 \ \rm V}$ als den Kreisradius ablesen.

(4)  Das Quellensignal $q(t)$ ist zum Zeitpunkt $t = 0$ maximal und damit auch die Phasenfunktion:

$$ \eta = \phi_{\rm max} = \phi( t =0) = \pi\hspace{0.15cm}\underline { = 3.1415} \hspace{0.05cm}.$$

Daraus erhält man für die Modulatorkonstante: $$K_{\rm PM} = \frac{\eta}{A_{\rm N}} = \frac{\pi}{2\,{\rm V}}\hspace{0.15cm}\underline {= 1.571\,{\rm V}^{-1}}\hspace{0.05cm}.$$

(5)  Man bewegt sich auf dem Kreis(bogen) im Uhrzeigersinn.

• Nach einem Viertel der Periodendauer  $T_{\rm N} = 1/f_{\rm N} = 200 \ \rm µ s$  ist  $ϕ(t) = 0$  und  $s_{\rm TP}(t) = 1 \ \rm V$.
• Zur Zeit  $t_1 = T_{\rm N}/2\hspace{0.15cm}\underline { = 100 \ \rm µ s}$  gilt  $ϕ(t_1) = -π$  und  $s_{\rm TP}(t_1) = -1 \ \rm V$.
• Danach bewegt man sich auf dem Kreisbogen entgegen dem Uhrzeigersinn.