Aufgaben:Exercise 1.2: Lognormal Channel Model

• Return to book

PDF of lognormal fading

We consider a mobile radio cell in an urban area and a vehicle that is approximately at a fixed distance  $d_0$  from the base station. For example, it moves on an arc around the base station.

Thus the total path loss can be described by the following equation: $$V_{\rm P} = V_{\rm 0} + V_{\rm S} \hspace{0.05cm}.$$

• $V_0$  takes into account the distance-dependent path loss which is assumed to be constant: $V_0 = 80 \ \rm dB$ .
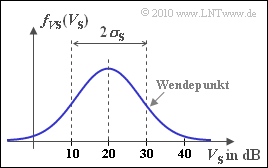
• The loss  $V_{\rm S}$  is due to shadowing caused by the lognormal–distribution with the probability density function (PDF)

$$f_{V{\rm S}}(V_{\rm S}) = \frac {1}{ \sqrt{2 \pi }\cdot \sigma_{\rm S}} \cdot {\rm exp } \left [ - \frac{ (V_{\rm S}- m_{\rm S})^2}{2 \cdot \sigma_{\rm S}^2} \right ] \hspace{0.05cm}$$

see diagram. The following numerical values apply:

$$m_{\rm S} = 20\,\,{\rm dB}\hspace{0.05cm},\hspace{0.2cm} \sigma_{\rm S} = 10\,\,{\rm dB}\hspace{0.15cm}{\rm or }\hspace{0.15cm}\sigma_{\rm S} = 0\,\,{\rm dB}\hspace{0.15cm}{\rm (subtask\hspace{0.15cm} 2)}\hspace{0.05cm}.$$

Also make the following simple assumptions:

• The transmit power is  $P_{\rm S} = 10 \ \rm W$  (or $40 \ \rm dBm$).
• The receive power should be at least  $P_{\rm E} = 10 \ \rm pW$  (or $–80 \ \rm dBm$)

Notes:

• This task belongs to the chapter  Distanzabhängige Dämpfung und Abschattung.

• You can use the following (rough) approximations for the complementary Gaussian error integral:

$${\rm Q}(1) \approx 0.16\hspace{0.05cm},\hspace{0.2cm} {\rm Q}(2) \approx 0.02\hspace{0.05cm},\hspace{0.2cm} {\rm Q}(3) \approx 10^{-3}\hspace{0.05cm}.$$

• Or use the interaction module provided by $\rm LNTwww$ Komplementäre Gaußsche Fehlerfunktionen.

Questionnaire

1

Would  $P_{\rm E}$  without consideration of the lognormal–fading be sufficient?

	Yes,
	No.

2

The parameters of the lognormal distribution are  $m_{\rm S} = 20 \, \rm dB$  and  $\sigma_{\rm S} = 0 \, \rm dB$. What percentage of the time does the system work?

${\rm Pr(System \ works)} \ = \ $ $\ \%$

3

What is the probability with  $m_{\rm S} = 20 \ \ \rm dB$  and  $\sigma_{\rm S} = 10 \ \ \rm dB$?

${\rm Pr(System \ works)}\ = \ $ $\ \%$

4

How big can  $V_0$  be at most, so that the reliability of   $99.9\%$  is reached?

$V_0 \ = \ $ $\ \ \rm dB$

Sample solution

Solution

(1)  The correct answer is YES:

• From the $\rm dB$–value $V_0 = 80 \ \rm dB$ follows the absolute (linear) value $K_0 = 10^8$. Thus the received power is

$$P_{\rm E} = P_{\rm S}/K_0 = 10 \ {\rm W}/10^8 = 100 \ {\rm nW} > 10 \ \ \rm pW.$$

• You can also solve this problem directly with the logarithmic quantities:

$10 \cdot {\rm lg}\hspace{0.15cm} \frac{P_{\rm E}}}{1\,\,{\rm mW}} = 10 \cdot {\rm lg}\hspace{0.15cm} \frac{P_{\rm S}}{1\,\,{\rm mW}} - V_0 = 40\,{\rm dBm} -80\,\,{\rm dB} = -40\,\,{\rm dBm} \hspace{0.05cm}.'"`UNIQ-MathJax19-QINU`"'{\rm Pr}({\rm "System\hspace{0.15cm} does not work\hspace{0.15cm}"})= {\rm Q}\left ( \frac{20\,\,{\rm dB}}}{\sigma_{\rm S} = 10\,{\rm dB}\right ) = {\rm Q}(2) \approx 0.02\hspace{0.3cm} \Rightarrow \hspace{0.3cm}{\rm Pr}({\rm "System\hspace{0.15cm} works"})= 1- 0.02 \hspace{0.15cm} \underline{\approx 98\,\%}\hspace{0.05cm}.'"`UNIQ-MathJax20-QINU`"'{\rm Pr}({\rm "System\hspace{0.15cm}funktioniert\hspace{0.15cm}nicht"})= {\rm Q}\left ( \frac{120-70-20}{10}\right ) = {\rm Q}(3) \approx 0.001 \hspace{0.05cm}.'"`UNIQ-MathJax21-QINU`"'{\rm Pr}({\rm "System\hspace{0.15cm} does not work\hspace{0.15cm}"})= {\rm Q}\left ( \frac{120-70-20}{10}\right ) = {\rm Q}(3) \approx 0.001 \hspace{0.05cm}.$$