Aufgaben:Exercise 2.3: Yet Another Multi-Path Channel

• Return to book

Vorgegebene Rechteckantwort

We consider a multipath channel, which is characterized by the following impulse response: $$h(\tau, \hspace{0.05cm} t) = h(\tau) = \sum_{m = 1}^{M} k_m \cdot \delta( \tau - \tau_m) \hspace{0.05cm}.$$

All coefficients  $k_{m}$  are real (positive or negative). Furthermore, we note

• From the specification  $h(\tau, \hspace{0.05cm}t) = h(\tau)$  you can see that the channel is time invariant.
• Generally, the channel has $M$ paths. The  value of $M$ should be determined from the graph.
• The following relations apply to the delay times:  $\tau_1 < \tau_2 < \tau_3 < \ \ text{...}$

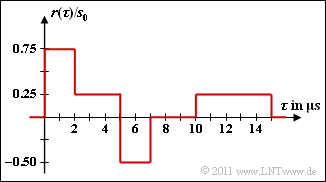
The graph shows the output signal  $r(\tau)$  of the channel when the following transmit signal is present at the input (shown in the equivalent low-pass range):

$$s(\tau) = \left\{ \begin{array}{c} s_0\\ 0 \end{array} \right.\quad \begin{array}{*{1}c} 0 \le \tau < 5\,{\rm µ s}, \\ {\rm otherwise}. \\ \end{array}$$

We want to find the corresponding impulse response  $h(\tau)$  as well as the transfer function  $H(f)$.

Notes:

• This task refers to the chapter  Mehrwegeempfang beim Mobilfunk.
• For the solution of subtask (1) assume that the impulse response  $h(\tau)$  has a span of 5 microseconds.

Questionnaire

1

What is the impulse response  $h(\tau)$? How many paths  $(M)$  are there?

$M \ = \ $

2

Specify the first three delays  $\tau_m$ .

$\tau_1 \ = \ $ $\ \ \rm µ s$

$\tau_2 \ = \ $ $\ \ \rm µ s$

$\tau_3 \ = \ $ $\ \ \rm µ s$

3

What are the weights of the first three Dirac impulses?

$k_1 \ = \ $

$k_2 \ = \ $

$k_3 \ = \ $

4

Calculate the frequency response  $H(f)$. What is the frequency period  $f_0$?
Note:   With integer  $i$, it must hold that   $H(f + i \cdot f_0) = H(f)$ .

$f_0 \ = \ $ $\ \ \rm kHz$

5

Calculate the magnitude of the frequency response. Which values result for the frequencies  $f = 0$,  $f = 250 \ \rm kHz$  and  $f = 500 \ \rm kHz$?

$|H(f = 0)| \ = \ $

$|H(f = 250 \ \rm kHz)| \ = \ $

$|H(f = 500 \ \rm kHz)| \ = \ $

6

What is the worst value  $({\rm worst \ case})$  for  $k_3$  at frequency  $f = 250 \ \rm kHz$?

$k_3 \ = \ $

Sample solution

Solution

(1)  Here $r(\tau) = s(\tau) ∗ h(\tau)$ is valid, where $s(\tau)$ denotes a rectangular pulse of duration $T = 5 \ \ \rm µ s$ and the impulse response $h(\tau)$ is generally made up of $M$ weighted Dirac functions at $\tau_1, \tau_2, \ \ \ \ text{...} \ , \tau_M$

The sketched output signal $r(\tau)$ can only result if

• $\tau_1 = 0$ (otherwise $r(\tau)$ would not start at $\tau = 0$),
• $\tau_M = 10 \ \ \rm µ s$ is (this results in the rectangular course between $10 \ \ \rm µ s$ and $15 \ \ \rm µ s$),
• in between another Dirac function at $\tau_2 = 2 \ \ \rm µ s$ occurs.

That means:   The impulse response here consists of $\underline {M = 3}$ Dirac functions.

(2)  As already calculated in the first subtask, one gets

$$\tau_1 \hspace{0.1cm} \underline {= 0}\hspace{0.05cm},\hspace{0.2cm}\tau_2 \hspace{0.1cm} \underline {= 2\,{\rm µ s}}\hspace{0.05cm},\hspace{0.2cm}\tau_3 \hspace{0.1cm} \underline {= 10\,{\rm µ s}}\hspace{0.05cm}.$$

(3)  If you compare input $s(\tau)$ and output $r(\tau)$, you will get the following results:

• Interval $0 < \tau < 2 \ {\rm µ s} \text \ \, s(\tau) = s_0, \hspace{1cm} r(\tau) = 0.75 \cdot s_0 \,\,\Rightarrow\,\, k_1 \ \underline {= 0.75}$,
• Interval $2 \ {\rm µ s} < \tau < 5 \ {\rm µ s} \text \ \, \hspace{2.4cm} r(\tau) =(k_1 + k_2) \cdot s_0 = 0.25 \cdot s_0 \Rightarrow k_2 \ \underline {= \, –0.50}$,
• interval $10 \ {\rm µ s} < \tau < 15 \ {\rm µ s} \text \ \,\hspace{\a6}{\a6} r(\tau} =k_3 \cdot s_0 = 0.25 \cdot s_0 \,\Rightarrow\, k_3 \ \underline {= 0.25}$.

(4)  With the displacement theorem one obtains for the Fourier transform of the impulse response $h(\tau)$: $$h(\tau) = k_1 \cdot \delta( \tau) + k_2 \cdot \delta( \tau - \tau_2)+ k_3 \cdot \delta( \tau - \tau_3) \hspace{0.3cm} \Rightarrow \hspace{0.3cm}H(f) = k_1 + k_2 \cdot {\rm e}^{- {\rm j}\cdot 2 \pi f \tau_2}+ k_3 \cdot {\rm e}^{- {\rm j}\cdot 2 \pi f \tau_3} \hspace{0.05cm}. $$

Analysis of the individual contributions leads to the following conclusion:

• The first share is constant  ⇒  period $f_1 → ∞$.
• The second share is periodic with $f_2 = 1/\tau_2 = 500 \ \rm kHz$.
• The third portion is periodic with $f_3 = 1/\thaw_3 = 100 \ \rm kHz$.

⇒   In total, $H(f)$ is thus periodic with $f_0 \ \underline {= 500 \ \ \rm kHz}$.

(5)  With $A = 2\pi f \cdot \tau_2$ and $B = 2\pi f \cdot \tau_3$ you get

$$|H(f)|^2 \hspace{-0.1cm} \ = \ \hspace{-0.1cm} H(f) \cdot H^{\star}(f)= \left [ \frac {3}{4} - \frac {1}{2} \cdot {\rm e}^{-{\rm j}A} + \frac {1}{4} \cdot {\rm e}^{-{\rm j}B}\right ] \left [ \frac {3}{4} - \frac {1}{2} \cdot {\rm e}^{{{\rm j}A} + \frac {1}{4} \cdot {\rm e}^{{\rm j}B}\right ]$ $$\Rightarrow \hspace{0.3cm} |H(f)|^2 \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \frac {9}{16}- \frac {3 {\rm e}^{{\rm j}A}}{8} +\frac {3{\rm e}^{{\rm j}B}}{16}

 - \frac {3{\rm e}^{-{\rm j}A}}{8} +\frac {1}{4}- \frac {{\rm e}^{{\rm j}(B-A)}}{8} +\frac {3{\rm e}^{-{\rm j}B}{16}  
 - \frac {{{\rm e}^{{{\rm j}(A-B)}}{8} +\frac{1}{16 }=$$
:$$\hspace{2.1cm} \ = \ \hspace{-0.1cm}\frac {7}{8}- \frac {3}{8} \cdot \left [ {\rm e}^{{\rm j}A} + {\rm e}^{-{\rm j}A}\right ]

\frac {3}{16} \cdot \left [ {\rm e}^{{\rm j}B} + {\rm e}^{-{\rm j}B}\right ]- \frac {1}{8} \cdot \left [ {\rm e}^{{{\rm j}(B-A)} + {\rm e}^{-{\rm j}(B-A)}\right ]\hspace{0.05cm}.$ This results in the [[Signal representation/For_calculation_with_complex_numbers#Depiction_by_amount_and_phase|set by Euler]] with consideration of the frequency periodicity: :'"`UNIQ-MathJax36-QINU`"' '"`UNIQ-MathJax37-QINU`"' :'"`UNIQ-MathJax38-QINU`"' '''(6)'''  The frequency response just calculated for the frequency $f = 250 \ \rm kHz$ can be displayed as follows: [[File:P_ID2162__Mob_A_2_3e.png|right|frame|Amplitude frequency response for three-way channel]] '"`UNIQ-MathJax39-QINU`"' If you now dial   :'"`UNIQ-MathJax40-QINU`"' the result is $|H(f = 250 \ \rm kHz)| = 0$ and thus the most unfavorable value for this signal frequency. The graph shows $|H(f)|$ in the range between $0$ and $500 \ \rm kHz$: *The blue curve applies to $k_3 = 0.25$ according to the specifications of subtask '''(4)''. *The red curve is valid for $k_3 = 1.25$, the most unfavourable value for $f = 250 \ \rm kHz$.