Aufgaben:Exercise 2.5: Scatter Function

• Return to book

Verzögerungs–Doppler–Funktion

For the mobile radio channel as a time-variant system, there are a total of four system functions that are linked with each other via the Fourier transform. With the nomenclature from our learning tutorial, these are:

• the time-variant impulse response  $h(\tau, \hspace{0.05cm}t)$, which we also denote here as  $\eta_{\rm VZ}(\tau,\hspace{0.05cm} t)$ ,
• the delay-Doppler function  $\eta_{\rm VD}(\tau,\hspace{0.05cm} f_{\rm D})$,
• the frequency-Doppler function  $\eta_{\rm FD}(f, \hspace{0.05cm}f_{\rm D})$,
• the time-variant transfer function  $\eta_{\rm FZ}(f,\hspace{0.05cm}t)$  or  $H(f, \hspace{0.05cm}t)$.

The indices represent the delay (V) $\tau$, the time (Z)   $t$, the frequency (F)  $f$  and the Doppler frequency (D)  $f_{\rm D}$.

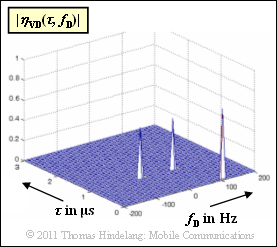
The delay–Doppler function  $\eta_{\rm VD}(\tau,\hspace{0.05cm} f_{\rm D})$  is shown in the top plot:

$$\eta_{\rm VD}(\tau, f_{\rm D}) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \frac{1}{\sqrt{2}} \cdot \delta (\tau) \cdot \delta (f_{\rm D} - 100\,{\rm Hz})-$$

$$\hspace{1.75cm} \ - \ \hspace{-0.1cm} \frac{1}{2} \cdot \delta (\tau- 1\,{\rm \mu s}) \cdot \delta (f_{\rm D} - 50\,{\rm Hz})- \frac{1}{2} \cdot \delta (\tau- 1\,{\rm \mu s}) \cdot \delta (f_{\rm D} + 50\,{\rm Hz}) \hspace{0.05cm}.$$

In the literature,  $\eta_{\rm VD}(\tau, \hspace{0.05cm}f_{\rm D})$  is often also called scatter function and denoted with  $s(\tau, \hspace{0.05cm}f_{\rm D})$ .

In this task, the associated delay–time function  $\eta_{\rm VZ}(\tau, \hspace{0.05cm}t)$  and the frequency–Doppler function  $\eta_{\rm FD}(f, \hspace{0.05cm}f_{\rm D})$  are to be determined.

Notes:

• This task should clarify the subject matter of the chapter  Das GWSSUS–Kanalmodell.
• The relationship between the individual system functions is given in the  graph on the first page  of this chapter.
• Note that the magnitude function  $|\eta_{\rm VD}(\tau, \hspace{0.05cm} f_{\rm D})|$  is shown above, so negative weights of the Dirac functions cannot be recognized.

Questionnaire

1

At which values of   $\tau$ are the components of 2D impulse response  $\eta_{\rm VZ}(\tau, \hspace{0.05cm}t)$ ?

	$\tau = 0$,
	$\tau = 1 \ \rm µ s$,
	other $\tau$–values.

2

Calculate  $|\eta_{\rm VZ}(\tau = 0,\hspace{0.05cm}t)|$. Which of the following statements are true?

	$|\eta_{\rm VZ}(\tau = 0,\hspace{0.05cm} t)|$  is independent of  $t$.
	$\eta_{\rm VZ}(\tau = 0, \hspace{0.05cm}t) = A \cdot \cos {(2\pi f_0 t)}$.
	$\eta_{\rm VZ}(\tau = 0, \hspace{0.05cm}t) = A \cdot \sin {(2\pi f_0 t)}$.

3

Calculate  $|\eta_{\rm VZ}(\tau = 1 \ {\rm µ s},\hspace{0.05cm} t)|$. Which of the following statements are true?

	$|\eta_{\rm VZ}(\tau = 1 \ {\rm µ s},\hspace{0.05cm} t)|$  is independent of  $t$.
	$\eta_{\rm VZ}(\tau = 1 \ {\rm µ s}, \hspace{0.05cm}t) = A \cdot \cos {(2\pi f_0 t)}$.
	$\eta_{\rm VZ}(\tau = 1 \ {\rm µ s}, \hspace{0.05cm}t) = A \cdot \sin {(2\pi f_0 t)}$.

4

Consider now the frequency–Doppler representation  $\eta_{\rm FD}(f, \hspace{0.05cm}f_{\rm D})$. For which values of   $f_{\rm D}$ is this function not equal to zero?

	$f_{\rm D} = 0$,
	$f_{\rm D} = ± 50 \ \rm Hz$,
	$f_{\rm D} = ± 100 \ \rm Hz$.

5

Which of the following statements are true for  $\eta_{\rm FD}(f,\hspace{0.05cm} f_{\rm D})$?

	$|\eta_{\rm FD}(f,\hspace{0.05cm} f_{\rm D} = 100 \ \rm Hz)|$  is independent of  $f_{\rm D}$.
	$\eta_{\rm FD}(f, \hspace{0.05cm} f_{\rm D} = 50 \ {\rm Hz}) = A \cdot \cos {(2\pi t_0 f)}$.
	$\eta_{\rm FD}(f, \hspace{0.05cm}f_{\rm D} = 50 \ {\rm Hz}) = A \cdot \sin {(2\pi t_0 f)}$.

6

How do you get the time-variant transfer function  $\eta_{\rm FZ}(f, \hspace{0.05cm}t)$?

	By Fourier transformation of  $\eta_{\rm VD}(\tau,\hspace{0.05cm} f_{\rm D})$  with respect to   $\tau$.
	By Fourier transformation of  $\eta_{\rm VZ}(\tau, \hspace{0.05cm}t)$  with respect to  $\tau$.
	By Fourier inverse transformation of  $\eta_{\rm FD}(f,\hspace{0.05cm} f_{\rm D})$  with respect to  $f_{\rm D}$.

Sample solution

Solution

(1)  The time-variant impulse response $h(\tau, \hspace{0.05cm} t) = \eta_{\rm VZ}(\tau, \hspace{0.05cm} t)$ is the inverse Fourier transform of the delay–Doppler function $\eta_{\rm VD}(\tau,\hspace{0.05cm} f_{\rm D}) = s(\tau, \hspace{0.05cm} f_{\rm D})$:

$$\eta_{\rm VZ}(\tau, \hspace{0.05cm} t) \hspace{0.2cm} \stackrel{t, \hspace{0.02cm}f_{\rm D}}{\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet} \hspace{0.2cm} \eta_{\rm VD}(\tau, f_{\rm D})\hspace{0.05cm}.$$

• Accordingly, $\eta_{\rm VZ}(\tau,\hspace{0.05cm} t)=0$ for the values of $\tau$ that make $\eta_{\rm VD}(\tau, f_{\rm D})=0$.
• The solutions 1 and 2 are therefore correct: Only for $\tau = 0$ and $\tau = 1 \ \ \rm \mu s$ does the time variant impulse response have nonzero values.

(2)  For the delay $\tau = 0$, the scatter function ($\eta_{\rm VD}$) consists of a single Dirac at $f_{\rm D} = 100 \ \rm Hz$.

• According to the second Fourier integral, the desired time-domain function satisfies:

$$\eta_{\rm VZ}(\tau = 0, t) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \frac{1}{\sqrt{2}} \cdot \int\limits_{-\infty}^{+\infty} \delta (f_{\rm D} - 100\,{\rm Hz}) \cdot {\rm e}^{{\rm j}\hspace{0.05cm}\cdot\hspace{0.05cm} 2 \pi f_{\rm D} t}\hspace{0.15cm}{\rm d}f_{\rm D} =\frac{1}{\sqrt{2}} \cdot {\rm e}^{ {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}2 \pi t \hspace{0.05cm}\cdot \hspace{0.05cm}100\,{\rm Hz}} .$$

• The correct solution is therefore solution 1.

(3)  For the delay $\tau = 1 \ \ \rm µ s$ the delay–Doppler function consists of two Dirac functions at $±50 \ \rm Hz$, each with weight $-0.5$.

• The time function is then

$$\eta_{\rm VZ}(\tau = 1\,{\rm \mu s}, t) = - \cos( 2 \pi t \cdot 50\,{\rm Hz})\hspace{0.05cm}.$$

• This function can be represented with $A = -1$ and $f_0 = 50 \ \rm Hz$ according to solution 2.

(4)  The three Dirac functions $\eta_{\rm VD}(\tau, \hspace{0.05cm}f_{\rm D})$ are at the Doppler frequencies $+100 \ \rm Hz$, $+50 \ \rm Hz$ and $-50 \ \rm Hz$.

• For all other Doppler frequencies, therefore, we must have $\eta_{\rm FD}(f, \hspace{0.05cm}f_{\rm D}) \equiv 0$.
• Solution 2 is therefore correct.

(5)'  If one looks at the scatter–function $\eta_{\rm VD}(\tau, \hspace{0.05cm}f_{\rm D})$ in the direction of the $\tau$–axis, one recognizes only one Dirac function each at the Doppler frequencies $100 \ \rm Hz$ and $±50 \ \rm Hz$.

• Here, depending on $f$, complex exponential oscillations with constant magnitude result in each case (from which it follows that the solution 1 is correct):

$$|\eta_{\rm FD}(f, \hspace{0.05cm}f_{\rm D} = 100\,{\rm Hz})| \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {1}/{\sqrt{2}} = {\rm const.}$$ $$| \eta_{\rm FD}(f, \hspace{0.05cm}f_{\rm D}= \pm 50\,{\rm Hz})| \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 0.5 = {\rm const.}$$

File:P ID2168 Mob A 2 5e new.png

interrelation of all system functions

(6)  As can be seen from the given Graphics, the solution alternatives 2 and 3 are applicable.

• The graphic shows all system functions.
• The Fourier correspondences (shown in green) illustrate the relationships between these system functions.

Note:

Compare the time-variant transfer function $|\eta_{\rm FZ}(f, \hspace{0.05cm} t)|$ in the figure below right with the corresponding graphic for Task 2.4:

• The respective amount functions shown differ significantly, although $|\eta_{\rm VZ}(\tau, t)|$ is the same in both cases.
• In task 2.4, a cosine was implicitly assumed for $\eta_{\rm VZ}(\tau = 1 \ {\rm µ s}, t)$, here a minus–cosine function.
• The (not explicitly) specified delay–Doppler function for task 2.4 was

$$\eta_{\rm VD}(\tau, f_{\rm D}) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \frac{1}{\sqrt{2} \cdot \delta (\tau) \cdot \delta (f_{\rm D} - 100\,{\rm Hz})+$ $$\hspace{2cm}+\hspace{0.22cm}\frac{1}{2} \cdot \delta (\tau- 1\,{\rm \mu s}) \cdot \delta (f_{\rm D} - 50\,{\rm Hz})+ $ '"`UNIQ-MathJax41-QINU`"' *Comparison with the equation on the [[Tasks:2.5_Scatter-Function|Specifications]] shows that only the signs of the Diracs have changed at $\tau = 1 \ \rm µ s$.