Difference between revisions of "Aufgaben:Exercise 4.15: MSK Compared with BPSK and QPSK"
From LNTwww
| Line 5: | Line 5: | ||
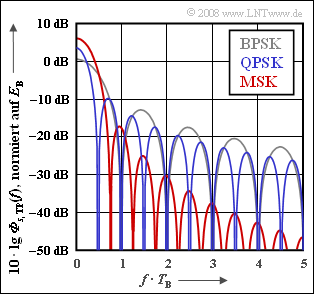
[[File:P_ID1745__Mod_A_4_14.png|right|frame|Leistungsdichtespektren: BPSK, QPSK, MSK]] | [[File:P_ID1745__Mod_A_4_14.png|right|frame|Leistungsdichtespektren: BPSK, QPSK, MSK]] | ||
Verglichen werden die Leistungsdichtespektren (im äquivalenten Tiefpassbereich) von | Verglichen werden die Leistungsdichtespektren (im äquivalenten Tiefpassbereich) von | ||
| − | * ''Binary Phase Shift Keying'' (BPSK), | + | * ''Binary Phase Shift Keying'' $\rm (BPSK)$, |
| − | * ''Quaternary Phase Shift Keying'' (QPSK), | + | * ''Quaternary Phase Shift Keying'' $\rm (QPSK)$, |
| − | * ''Minimum Shift Keying'' (MSK). | + | * ''Minimum Shift Keying'' $\rm (MSK)$. |
| Line 13: | Line 13: | ||
| − | Für die BPSK und die QPSK ist jeweils ein rechteckförmiger Grundimpuls der Höhe $s_0$ und der Symboldauer $T$ vorausgesetzt. Damit gilt für die BPSK und die QPSK (bzw. die 4–QAM und die Offset–QPSK) gleichermaßen: | + | Für die BPSK und die QPSK ist jeweils ein rechteckförmiger Grundimpuls der Höhe $s_0$ und der Symboldauer $T$ vorausgesetzt. Damit gilt für die BPSK und die QPSK (bzw. die 4–QAM und die Offset–QPSK) gleichermaßen: |
:$${\it \Phi}_{s}(f) = \frac{s_0^2 \cdot T}{4} \cdot \big [ {\rm si}^2 ( \pi T \cdot (f- f_{\rm T}) ) + {\rm si}^2 ( \pi T \cdot (f+ f_{\rm T}) ) \big ]\hspace{0.05cm},$$ | :$${\it \Phi}_{s}(f) = \frac{s_0^2 \cdot T}{4} \cdot \big [ {\rm si}^2 ( \pi T \cdot (f- f_{\rm T}) ) + {\rm si}^2 ( \pi T \cdot (f+ f_{\rm T}) ) \big ]\hspace{0.05cm},$$ | ||
und in den äquivalenten Tiefpassbereich transformiert: | und in den äquivalenten Tiefpassbereich transformiert: | ||
| Line 19: | Line 19: | ||
Trotz gleicher Formel weisen die BPSK und die QPSK unterschiedliche Leistungsdichtespektren auf: | Trotz gleicher Formel weisen die BPSK und die QPSK unterschiedliche Leistungsdichtespektren auf: | ||
| − | *Bei der BPSK (graue Kurve) ist die Symboldauer $T$ gleich der Bitdauer $T_{\rm B}$ und es gilt mit der Energie pro Bit $(E_{\rm B} = s_0^2 · T_{\rm B}/2)$ : | + | *Bei der BPSK (graue Kurve) ist die Symboldauer $T$ gleich der Bitdauer $T_{\rm B}$ und es gilt mit der Energie pro Bit $(E_{\rm B} = s_0^2 · T_{\rm B}/2)$ : |
:$${\it \Phi}_{s,\hspace{0.05cm} {\rm TP}}(f) = E_{\rm B} \cdot {\rm si}^2 ( \pi f T_{\rm B} ) \hspace{0.05cm}.$$ | :$${\it \Phi}_{s,\hspace{0.05cm} {\rm TP}}(f) = E_{\rm B} \cdot {\rm si}^2 ( \pi f T_{\rm B} ) \hspace{0.05cm}.$$ | ||
*Dagegen ist bei der QPSK (blaue Kurve) bei gleichem $E_{\rm B}$ die Symboldauer $T$ doppelt so groß: | *Dagegen ist bei der QPSK (blaue Kurve) bei gleichem $E_{\rm B}$ die Symboldauer $T$ doppelt so groß: | ||
| Line 26: | Line 26: | ||
Bei der Berechnung des MSK–Spektrums (rote Kurve) kann berücksichtigt werden, dass die MSK als Offset–QPSK entsprechend dem [[Modulationsverfahren/Nichtlineare_Modulationsverfahren#Realisierung_der_MSK_als_Offset.E2.80.93QPSK_.281.29|Blockschaltbild]] im Theorieteil realisiert werden kann, wenn der folgende Grundimpuls verwendet wird: | Bei der Berechnung des MSK–Spektrums (rote Kurve) kann berücksichtigt werden, dass die MSK als Offset–QPSK entsprechend dem [[Modulationsverfahren/Nichtlineare_Modulationsverfahren#Realisierung_der_MSK_als_Offset.E2.80.93QPSK_.281.29|Blockschaltbild]] im Theorieteil realisiert werden kann, wenn der folgende Grundimpuls verwendet wird: | ||
| − | :$$g(t) = \left\{ \begin{array}{l} g_0 \cdot \cos ( | + | :$$g(t) = \left\{ \begin{array}{l} g_0 \cdot \cos (\pi/2 \cdot t/T) \\ 0 \\ \end{array} \right.\quad \begin{array}{*{5}c}{\rm{f\ddot{u}r}} \\{\rm{f\ddot{u}r}} \\ \end{array}\begin{array}{*{10}c} -T \le t \le +T \hspace{0.05cm}, \\ {\rm sonst}\hspace{0.05cm}. \\ \end{array}$$ |
In der [[Aufgaben:4.15Z_MSK–Grundimpuls_und_MSK-Spektrum|Aufgabe 4.14Z]] wird die zugehörige Spektralfunktion berechnet: | In der [[Aufgaben:4.15Z_MSK–Grundimpuls_und_MSK-Spektrum|Aufgabe 4.14Z]] wird die zugehörige Spektralfunktion berechnet: | ||
:$$G(f) = \frac {4}{\pi}\cdot g_0 \cdot T \cdot \frac{ {\rm cos} ( 2 \pi f T )}{1 - (4 f T)^2 }\hspace{0.05cm}.$$ | :$$G(f) = \frac {4}{\pi}\cdot g_0 \cdot T \cdot \frac{ {\rm cos} ( 2 \pi f T )}{1 - (4 f T)^2 }\hspace{0.05cm}.$$ | ||
| Line 35: | Line 35: | ||
* Auch bei MSK ist die Energie pro Bit wie folgt gegeben: $E_{\rm B} = s_0^2 · T/2$. | * Auch bei MSK ist die Energie pro Bit wie folgt gegeben: $E_{\rm B} = s_0^2 · T/2$. | ||
* Der Betrag des Tiefpass–Signals $|s_{\rm TP}(t)| = s_0$ ist gleich dem Maximalwert $g_0$ des Grundimpulses $g(t)$. | * Der Betrag des Tiefpass–Signals $|s_{\rm TP}(t)| = s_0$ ist gleich dem Maximalwert $g_0$ des Grundimpulses $g(t)$. | ||
| + | |||
| + | |||
| + | |||
| Line 52: | Line 55: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {Bei welcher Frequenz $f_1$ hat das BPSK–Leistungsdichtespektrum seine erste Nullstelle? Der Bezugswert ist die Bitrate $1/T_{\rm B}$. | + | {Bei welcher Frequenz $f_1$ hat das BPSK–Leistungsdichtespektrum seine erste Nullstelle? Der Bezugswert ist die Bitrate $1/T_{\rm B}$. |
|type="{}"} | |type="{}"} | ||
$f_1 \ = \ $ { 1 3% } $\ \cdot 1/T_{\rm B}$ | $f_1 \ = \ $ { 1 3% } $\ \cdot 1/T_{\rm B}$ | ||
| Line 60: | Line 63: | ||
$f_1 \ = \ $ { 0.5 3% } $\ \cdot 1/T_{\rm B}$ | $f_1 \ = \ $ { 0.5 3% } $\ \cdot 1/T_{\rm B}$ | ||
| − | {Wie lautet das MSK–Leistungsdichtespektrum im äquivalenten TP–Bereich? Welcher LDS–Wert $($normiert auf $E_{\rm B})$ tritt bei $f = 0$ auf? | + | {Wie lautet das MSK–Leistungsdichtespektrum im äquivalenten TP–Bereich? Welcher LDS–Wert $($normiert auf $E_{\rm B})$ tritt bei $f = 0$ auf? |
|type="{}"} | |type="{}"} | ||
${\itΦ}_\text{s, TP}(f = 0) \ = \ $ { 3.243 3% } $\ \cdot E_{\rm B}$ | ${\itΦ}_\text{s, TP}(f = 0) \ = \ $ { 3.243 3% } $\ \cdot E_{\rm B}$ | ||
| Line 67: | Line 70: | ||
|type="[]"} | |type="[]"} | ||
- Die erste LDS–Nullstelle kommt bei MSK früher als bei QPSK. | - Die erste LDS–Nullstelle kommt bei MSK früher als bei QPSK. | ||
| − | + Das MSK–Leistungsdichtespektrum klingt schneller ab. | + | + Das MSK–Leistungsdichtespektrum klingt schneller ab im Vergleich zur QPSK. |
| − | - Bei MSK ist das Integral über ${\itΦ}_\text{s, TP}(f)$ (nicht logarithmiert) größer als bei QPSK. | + | - Bei MSK ist das Integral über ${\itΦ}_\text{s, TP}(f)$ (nicht logarithmiert!) größer als bei QPSK. |
</quiz> | </quiz> | ||
Revision as of 12:47, 24 April 2020
Leistungsdichtespektren: BPSK, QPSK, MSK
Verglichen werden die Leistungsdichtespektren (im äquivalenten Tiefpassbereich) von
- Binary Phase Shift Keying $\rm (BPSK)$,
- Quaternary Phase Shift Keying $\rm (QPSK)$,
- Minimum Shift Keying $\rm (MSK)$.
Diese sind in der Grafik logarithmisch dargestellt, wobei die Frequenz auf den Kehrwert der Bitdauer $T_{\rm B}$ normiert ist.
Für die BPSK und die QPSK ist jeweils ein rechteckförmiger Grundimpuls der Höhe $s_0$ und der Symboldauer $T$ vorausgesetzt. Damit gilt für die BPSK und die QPSK (bzw. die 4–QAM und die Offset–QPSK) gleichermaßen:
- $${\it \Phi}_{s}(f) = \frac{s_0^2 \cdot T}{4} \cdot \big [ {\rm si}^2 ( \pi T \cdot (f- f_{\rm T}) ) + {\rm si}^2 ( \pi T \cdot (f+ f_{\rm T}) ) \big ]\hspace{0.05cm},$$
und in den äquivalenten Tiefpassbereich transformiert:
- $$ {\it \Phi}_{s,\hspace{0.05cm} {\rm TP}}(f) = \frac{s_0^2 \cdot T}{2} \cdot {\rm si}^2 ( \pi f T ) \hspace{0.05cm}.$$
Trotz gleicher Formel weisen die BPSK und die QPSK unterschiedliche Leistungsdichtespektren auf:
- Bei der BPSK (graue Kurve) ist die Symboldauer $T$ gleich der Bitdauer $T_{\rm B}$ und es gilt mit der Energie pro Bit $(E_{\rm B} = s_0^2 · T_{\rm B}/2)$ :
- $${\it \Phi}_{s,\hspace{0.05cm} {\rm TP}}(f) = E_{\rm B} \cdot {\rm si}^2 ( \pi f T_{\rm B} ) \hspace{0.05cm}.$$
- Dagegen ist bei der QPSK (blaue Kurve) bei gleichem $E_{\rm B}$ die Symboldauer $T$ doppelt so groß:
- $${\it \Phi}_{s,\hspace{0.05cm} {\rm TP}}(f) = 2 \cdot E_{\rm B} \cdot {\rm si}^2 ( 2\pi f T_{\rm B} ) \hspace{0.05cm}.$$
Bei der Berechnung des MSK–Spektrums (rote Kurve) kann berücksichtigt werden, dass die MSK als Offset–QPSK entsprechend dem Blockschaltbild im Theorieteil realisiert werden kann, wenn der folgende Grundimpuls verwendet wird:
- $$g(t) = \left\{ \begin{array}{l} g_0 \cdot \cos (\pi/2 \cdot t/T) \\ 0 \\ \end{array} \right.\quad \begin{array}{*{5}c}{\rm{f\ddot{u}r}} \\{\rm{f\ddot{u}r}} \\ \end{array}\begin{array}{*{10}c} -T \le t \le +T \hspace{0.05cm}, \\ {\rm sonst}\hspace{0.05cm}. \\ \end{array}$$
In der Aufgabe 4.14Z wird die zugehörige Spektralfunktion berechnet:
- $$G(f) = \frac {4}{\pi}\cdot g_0 \cdot T \cdot \frac{ {\rm cos} ( 2 \pi f T )}{1 - (4 f T)^2 }\hspace{0.05cm}.$$
Berücksichtigen Sie weiterhin:
- Die beiden Signale $s_{\rm I}(t)$ und $s_{\rm Q}(t)$ sind trotz der Vorcodierung unkorreliert.
- Bei MSK ist entgegen der QPSK wie bei der BPSK $T = T_{\rm B}$ zu setzen.
- Auch bei MSK ist die Energie pro Bit wie folgt gegeben: $E_{\rm B} = s_0^2 · T/2$.
- Der Betrag des Tiefpass–Signals $|s_{\rm TP}(t)| = s_0$ ist gleich dem Maximalwert $g_0$ des Grundimpulses $g(t)$.
Hinweise:
- Die Aufgabe gehört zum Kapitel Nichtlineare digitale Modulation.
- Bezug genommen wird insbesondere auf den Abschnitt Realisierung der MSK als Offset-QPSK.
- Das Leistungsdichtespektrums im äquivalenten Tiefpassbereich eines Zweiges – zum Beispiel: Inphasekomponente – lautet:
- $${\it \Phi}_{s,\hspace{0.05cm} {\rm I},\hspace{0.05cm} {\rm TP}}(f) = \frac{1}{2 T} \cdot {\rm E} \left [ a_\nu ^2 \right ] \cdot |G(f)|^2 \hspace{0.05cm}.$$
Fragebogen
Musterlösung
(1) Aus der angegebenen Gleichung und der Grafik erkennt man, dass bei Binary Phase Shift Keying (BPSK) die erste Nullstelle des Leistungsdichtespektrums bei $f_1\hspace{0.15cm}\underline{ =1} \cdot 1/T_{\rm B}$ liegt.
(2) Aufgrund der niedrigeren Symbolrate $1/T$ ist bei Quaternary Phase Shift Keying (QPSK) – und bei allen verwandten quaternären Modulationsverfahren – das Spektrum nur halb so breit wie bei der BPSK ⇒ $f_1\hspace{0.15cm}\underline{ =0.5} \cdot 1/T_{\rm B}$.
(3) Für das Leistungsdichtespektren (LDS) des Gesamtsignals gilt im äquivalenten Tiefpassbereich:
- $${\it \Phi}_{s,\hspace{0.05cm} {\rm TP}}(f) = {\it \Phi}_{s,\hspace{0.05cm} {\rm I},\hspace{0.05cm} {\rm TP}}(f) + {\it \Phi}_{s,\hspace{0.05cm} {\rm Q},\hspace{0.05cm} {\rm TP}}(f)= 2 \cdot {\it \Phi}_{s,\hspace{0.05cm} {\rm I},\hspace{0.05cm} {\rm TP}}(f) = {1}/{ T} \cdot |G(f)|^2\hspace{0.05cm}.$$
Hierbei ist berücksichtigt, dass
- die Signale $s_{\rm I}(t)$ und $s_{\rm Q}(t)$ unkorreliert sind, so dass man die LDS–Anteile addieren kann,
- wegen der binären bipolaren Amplitudenkoeffizienten der Erwartungswert $E[a_ν^2] = 1$ ist.
Damit erhält man:
- $${\it \Phi}_{s,\hspace{0.05cm} {\rm TP}}(f)= \frac{1}{ T} \cdot \left ( \frac {4}{\pi} \right ) ^2 \cdot g_0^2 \cdot T^2 \cdot \frac{ {\rm cos}^2 ( 2 \pi f T )}{ \big [1 - (4 f T)^2 \big ] ^2} \hspace{0.05cm}.$$
Mit $s_0 = g_0$, $T = T_{\rm B}$ und $E_{\rm B} = s_0^2 · T_{\rm B}/2$ gilt weiter:
- $${\it \Phi}_{s,\hspace{0.05cm} {\rm TP}}(f)= \frac{32}{ \pi^2} \cdot E_{\rm B} \cdot \frac{ {\rm cos}^2 ( 2 \pi \cdot f \cdot T_{\rm B} )}{ \big [1 - (4 \cdot f \cdot T_{\rm B})^2 \big ] ^2}\hspace{0.3cm} \Rightarrow \hspace{0.3cm} {\it \Phi}_{s,\hspace{0.05cm} {\rm TP}}(f = 0 )= \frac{32}{ \pi^2} \cdot E_{\rm B} \hspace{0.15cm}\underline {\approx 3.243 \cdot E_{\rm B}} \hspace{0.05cm}.$$
(4) Richtig ist nur der Lösungsvorschlag 1:
- Bereits aus der Grafik ist zu ersehen, dass die erste Aussage falsch und die zweite richtig ist.
- Der Lösungsvorschlag 3 stimmt ebenfalls nicht. Das Integral über die Leistungsdichtespektren ergibt die Leistung $(E_{\rm B}/T_{\rm B})$.
- Die Signalverläufe von BPSK, QPSK und MSK machen deutlich, dass die Leistung bei konstanter Hüllkurve $(s_0)$ für alle betrachteten Modulationsverfahren gleich ist.
