Difference between revisions of "Aufgaben:3.3Z Einfacher Phasenmodulator"
(Die Seite wurde neu angelegt: „ {{quiz-Header|Buchseite=Modulationsverfahren/Phasenmodulation (PM) }} [[File:|right|]] ===Fragebogen=== <quiz display=simple> {Multiple-Choice Frage |typ…“) |
m (Text replacement - "[File:" to "[File:") |
||
| (2 intermediate revisions by one other user not shown) | |||
| Line 3: | Line 3: | ||
}} | }} | ||
| − | [[File:|right|]] | + | [[File:P_ID1086__Mod_A_3_4.png|right|]] |
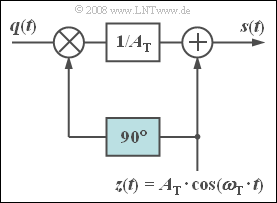
| + | Die nebenstehende Schaltung erlaubt die näherungsweise Realisierung eines phasenmodulierten Signals. Der 90°– Phasenschieber formt aus dem cosinusförmigen Träger $z(t)$ ein Sinussignal gleicher Frequenz, so dass für das modulierte Signal geschrieben werden kann: | ||
| + | $$ s(t) = z(t) + q(t) \cdot \frac{z(t- T_0/4)}{A_{\rm T}} =\hspace{0.45cm}$$ | ||
| + | $$= A_{\rm T} \cdot \cos (\omega_{\rm T} \cdot t) + q(t) \cdot \sin (\omega_{\rm T} \cdot t) \hspace{0.05cm}.$$ | ||
| + | Der zweite Term beschreibt eine ZSB–AM ohne Träger. Zusätzlich wird der um 90° phasenverschobene Träger addiert. Bei cosinusförmigem Quellensignal | ||
| + | $$q(t) = A_{\rm N} \cdot \cos (\omega_{\rm N} \cdot t)$$ | ||
| + | ergibt sich somit: | ||
| + | $$s(t) = A_{\rm T} \cdot \cos (\omega_{\rm T} \cdot t) + A_{\rm N} \cdot \cos (\omega_{\rm N} \cdot t) \cdot \sin (\omega_{\rm T} \cdot t) =$$ | ||
| + | $$ = A_{\rm T} \cdot \left[\cos (\omega_{\rm T} \cdot t) + \eta \cdot \cos (\omega_{\rm N} \cdot t) \cdot \sin (\omega_{\rm T} \cdot t) \right] \hspace{0.05cm}.$$ | ||
| + | Hierbei bezeichnen wir das Verhältnis $η = A_N/A_T$ als den Modulationsindex; die Trägeramplitude wird im Folgenden zur Vereinfachung $A_T = 1$ gesetzt. | ||
| + | |||
| + | Im Gegensatz zur idealen '''PM''' unterscheidet sich bei dieser näherungsweisen Phasenmodulation $η$ vom Phasenhub $ϕ_{max}$. Außerdem werden Sie erkennen, dass die Hüllkurve $a(t) ≠ 1$ ist. Das bedeutet, dass hier der Phasenmodulation eine unerwünschte Amplitudenmodulation überlagert ist. | ||
| + | |||
| + | Berechnet werden sollen in dieser Aufgabe aus der Darstellung des äquivalenten TP–Signals $s_{TP}(t)$ in der komplexen Ebene (Ortskurve) die Hüllkurve $a(t)$ und die Phasenfunktion $ϕ(t)$. Außerdem sollen die Verfälschungen analysiert werden, die sich ergeben, wenn bei diesem nichtidealen Modulator ein idealer Phasendemodulator zugrundegelegt wird, der das Sinkensignal $υ(t)$ proportional zur Phase $ϕ(t)$ setzt. | ||
| + | |||
| + | '''Hinweis:''' Diese Aufgabe bezieht sich auf den Theorieteil von [http://en.lntwww.de/Modulationsverfahren/Phasenmodulation_(PM) Kapitel 3.1]. Zur näherungsweisen Berechnung des Klirrfaktors können Sie folgende Gleichungen benutzen: | ||
| + | $$\arctan(\gamma) \approx \gamma - {\gamma^3}/{3} \hspace{0.05cm}, \hspace{0.3cm} \cos^3(\gamma) ={3}/{4} \cdot \cos(\gamma) +{1}/{4} \cdot \cos(3 \cdot \gamma) \hspace{0.05cm}.$$ | ||
| Line 9: | Line 25: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Berechnen Sie das äquivalente TP–Signal. Welche Aussage trifft zu? |
|type="[]"} | |type="[]"} | ||
| − | - | + | - Die Ortskurve $s_{TP}(t)$ ist ein Kreisbogen. |
| − | + | + | - Die Ortskurve $s_{TP}(t)$ ist eine horizontale Gerade. |
| + | + Die Ortskurve $s_{TP}(t)$ ist eine vertikale Gerade. | ||
| + | |||
| + | |||
| + | {Berechnen Sie die (normierte) Hüllkurve $a(t)$ für $A_T = 1$. Wie groß sind deren Minimal– und Maximalwert mit $η = 1$? | ||
| + | |type="{}"} | ||
| + | $η = 1: a_{min}$ = { 1 3% } | ||
| + | $η = 1: a_{max}$ = { 1.414 3% } | ||
| + | {Berechnen Sie den Maximalwert der Phase $ϕ(t)$ für $η = 1$ und $η = 0.5$. | ||
| + | |type="{}"} | ||
| + | $ η = 1: ϕ_{max}$ = { 45 3% } $Grad$ | ||
| + | $ η = 0.5: ϕ_{max}$ = { 26.6 3% } $Grad$ | ||
| − | { | + | {Welche Verzerrungen ergeben sich nach idealer Phasendemodulation von $s(t)$? |
| + | |type="[]"} | ||
| + | - Es treten keine Verzerrungen auf. | ||
| + | - Es treten lineare Verzerrungen auf. | ||
| + | + Es treten nichtlineare Verzerrungen auf. | ||
| + | |||
| + | {Berechnen Sie den Klirrfaktor unter Berücksichtigung der auf der Angabenseite genannten trigonometrischen Beziehungen. | ||
|type="{}"} | |type="{}"} | ||
| − | $\ | + | $η = 1: K$ = { 11.1 3% } $\text{%}$ |
| + | $η = 0.5: K$ = { 2.2 3% } $\text{%}$ | ||
| + | |||
| Line 25: | Line 60: | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
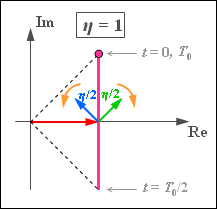
| − | '''1.''' | + | '''1.''' Das äquivalente Tiefpass–Signal lautet: |
| − | '''2.''' | + | $$s_{\rm TP}(t) = A_{\rm T} \cdot \left ( 1 + {\rm j}\cdot \frac {\eta}{2}\cdot \left ({\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}\omega_{\rm N} \hspace{0.05cm}\cdot \hspace{0.05cm} t} + {\rm e}^{\hspace{0.05cm}{-\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}\omega_{\rm N} \hspace{0.05cm}\cdot \hspace{0.05cm} t}\right) \right)$$ |
| − | '''3.''' | + | $$ = A_{\rm T} \cdot \left ( 1 + {\rm j}\cdot {\eta}\cdot \cos (\omega_{\rm N} \cdot t) \right)\hspace{0.05cm}.$$ |
| − | '''4.''' | + | [[File:P_ID1087__Mod_A_3_4_a.png|right|]] |
| − | '''5.''' | + | Die Grafik verdeutlicht, dass die Ortskurve $s_{TP}(t)$ nun eine vertikale Gerade ist im Gegensatz zur idealen PM (Kreisbogen) und zur ZSB–AM (horizontale Gerade). Im Folgenden wird $A_T = 1$ gesetzt. |
| − | + | ||
| − | + | ||
| + | '''2.''' Die Hüllkurve ergibt sich aus der zeitabhängigen Zeigerlänge zu | ||
| + | $$a(t) = \sqrt{1 + \eta^2 \cdot \cos^2 (\omega_{\rm N} \cdot t)}$$ | ||
| + | $$ \Rightarrow \hspace{0.3cm}a_{\rm min} \hspace{0.15cm}\underline { = 1}, \hspace{0.3cm}a_{\rm max} = \sqrt{1 + \eta^2 }\hspace{0.05cm}.$$ | ||
| + | Für $η = 1$ hat amax den Wert $2^{0.5} ≈ 1.414$. | ||
| + | |||
| + | |||
| + | '''3.''' Für die Phasenfunktion gilt: | ||
| + | $$\phi(t) = \arctan \frac{{\rm Im}[s_{\rm TP}(t)]}{{\rm Re}[s_{\rm TP}(t)]} = \arctan (\eta \cdot \cos (\omega_{\rm N} \cdot t)) \hspace{0.05cm}.$$ | ||
| + | Der Maximalwert tritt beispielsweise zur Zeit $t = 0$ auf und beträgt $ϕ_{max} = arctan(η)$. Für $η = 1$ erhält man $ϕ_{max} = 45°$ (bei idealer PM $57.3°$) und für $η = 0.5$ ergibt sich $ϕ_{max} = 26.6°$ (ideale PM: $28.7°$). | ||
| + | |||
| + | |||
| + | '''4.'''Es gilt nicht arctan$(η · cos(γ)) = η · cos(γ)$. Das heißt, dass das Sinkensignal im Gegensatz zum Quellensignal nicht cosinusförmig verläuft. Dies weist auf $\underline{nichtlineare Verzerrungen}$ hin ⇒ $\underline{Vorschlag 3}$. | ||
| + | |||
| + | |||
| + | '''5.''' Mit $γ = η · cos(ω_N · t)$ und $arctan(γ) ≈ γ – γ^3/3$ erhält man | ||
| + | $$ \phi(t) = \eta \cdot \cos (\omega_{\rm N} \cdot t) - \frac{\eta^3}{3}\cdot \cos^3 (\omega_{\rm N} \cdot t))=$$ | ||
| + | $$ = \eta \cdot \cos (\omega_{\rm N} \cdot t) - \frac{\eta^3}{3}\cdot \left [ \frac{3}{4}\cdot \cos (\omega_{\rm N} \cdot t) + \frac{1}{4}\cdot \cos (3 \omega_{\rm N} \cdot t)\right ] =$$ | ||
| + | $$ = \left(\eta - \frac{\eta^3}{4} \right) \cdot \cos (\omega_{\rm N} \cdot t) - \frac{\eta^3}{12}\cdot \cos (3\omega_{\rm N} \cdot t)) \hspace{0.05cm}.$$ | ||
| + | Das bedeutet: Bei Verwendung der angegebenen Reihenentwicklung (Terme 5. und höherer Ordnung werden vernachlässigt) ist nur der Klirrfaktor dritter Ordnung von 0 verschieden. Man erhält: | ||
| + | $$K = K_3 = \frac{\eta^3/12}{\eta-\eta^3/4}= \frac{1}{12/\eta^2 -3} \hspace{0.05cm}.$$ | ||
| + | Für $η = 1$ ergibt sich der Zahlenwert $K = 1/9 ≈ 11.1%$. Für $η = 0.5$ ist der Klirrfaktor $K = 1/45 ≈ 2.2%$. | ||
| + | |||
| + | Eine Simulation zeigt, dass man durch den Abbruch der Reihe nach dem Term dritter Ordnung einen Fehler macht, der den Klirrfaktor als zu hoch erscheinen lässt. Die per Simulation gewonnenen Werte sind $K ≈ 6%$ (für $η = 1$) und $K ≈ 2%$ (für $η = 0.5$). Der Fehler nimmt also mit wachsendem η mehr als proportional zu. | ||
| + | |||
{{ML-Fuß}} | {{ML-Fuß}} | ||
| − | [[Category:Aufgaben | + | [[Category:Aufgaben zuModulationsverfahren|^3.1 Phasenmodulation (PM)^]] |
Latest revision as of 15:09, 26 May 2020
Die nebenstehende Schaltung erlaubt die näherungsweise Realisierung eines phasenmodulierten Signals. Der 90°– Phasenschieber formt aus dem cosinusförmigen Träger $z(t)$ ein Sinussignal gleicher Frequenz, so dass für das modulierte Signal geschrieben werden kann: $$ s(t) = z(t) + q(t) \cdot \frac{z(t- T_0/4)}{A_{\rm T}} =\hspace{0.45cm}$$ $$= A_{\rm T} \cdot \cos (\omega_{\rm T} \cdot t) + q(t) \cdot \sin (\omega_{\rm T} \cdot t) \hspace{0.05cm}.$$ Der zweite Term beschreibt eine ZSB–AM ohne Träger. Zusätzlich wird der um 90° phasenverschobene Träger addiert. Bei cosinusförmigem Quellensignal $$q(t) = A_{\rm N} \cdot \cos (\omega_{\rm N} \cdot t)$$ ergibt sich somit: $$s(t) = A_{\rm T} \cdot \cos (\omega_{\rm T} \cdot t) + A_{\rm N} \cdot \cos (\omega_{\rm N} \cdot t) \cdot \sin (\omega_{\rm T} \cdot t) =$$ $$ = A_{\rm T} \cdot \left[\cos (\omega_{\rm T} \cdot t) + \eta \cdot \cos (\omega_{\rm N} \cdot t) \cdot \sin (\omega_{\rm T} \cdot t) \right] \hspace{0.05cm}.$$ Hierbei bezeichnen wir das Verhältnis $η = A_N/A_T$ als den Modulationsindex; die Trägeramplitude wird im Folgenden zur Vereinfachung $A_T = 1$ gesetzt.
Im Gegensatz zur idealen PM unterscheidet sich bei dieser näherungsweisen Phasenmodulation $η$ vom Phasenhub $ϕ_{max}$. Außerdem werden Sie erkennen, dass die Hüllkurve $a(t) ≠ 1$ ist. Das bedeutet, dass hier der Phasenmodulation eine unerwünschte Amplitudenmodulation überlagert ist.
Berechnet werden sollen in dieser Aufgabe aus der Darstellung des äquivalenten TP–Signals $s_{TP}(t)$ in der komplexen Ebene (Ortskurve) die Hüllkurve $a(t)$ und die Phasenfunktion $ϕ(t)$. Außerdem sollen die Verfälschungen analysiert werden, die sich ergeben, wenn bei diesem nichtidealen Modulator ein idealer Phasendemodulator zugrundegelegt wird, der das Sinkensignal $υ(t)$ proportional zur Phase $ϕ(t)$ setzt.
Hinweis: Diese Aufgabe bezieht sich auf den Theorieteil von Kapitel 3.1. Zur näherungsweisen Berechnung des Klirrfaktors können Sie folgende Gleichungen benutzen: $$\arctan(\gamma) \approx \gamma - {\gamma^3}/{3} \hspace{0.05cm}, \hspace{0.3cm} \cos^3(\gamma) ={3}/{4} \cdot \cos(\gamma) +{1}/{4} \cdot \cos(3 \cdot \gamma) \hspace{0.05cm}.$$
Fragebogen
Musterlösung
Die Grafik verdeutlicht, dass die Ortskurve $s_{TP}(t)$ nun eine vertikale Gerade ist im Gegensatz zur idealen PM (Kreisbogen) und zur ZSB–AM (horizontale Gerade). Im Folgenden wird $A_T = 1$ gesetzt.
2. Die Hüllkurve ergibt sich aus der zeitabhängigen Zeigerlänge zu
$$a(t) = \sqrt{1 + \eta^2 \cdot \cos^2 (\omega_{\rm N} \cdot t)}$$
$$ \Rightarrow \hspace{0.3cm}a_{\rm min} \hspace{0.15cm}\underline { = 1}, \hspace{0.3cm}a_{\rm max} = \sqrt{1 + \eta^2 }\hspace{0.05cm}.$$
Für $η = 1$ hat amax den Wert $2^{0.5} ≈ 1.414$.
3. Für die Phasenfunktion gilt:
$$\phi(t) = \arctan \frac{{\rm Im}[s_{\rm TP}(t)]}{{\rm Re}[s_{\rm TP}(t)]} = \arctan (\eta \cdot \cos (\omega_{\rm N} \cdot t)) \hspace{0.05cm}.$$
Der Maximalwert tritt beispielsweise zur Zeit $t = 0$ auf und beträgt $ϕ_{max} = arctan(η)$. Für $η = 1$ erhält man $ϕ_{max} = 45°$ (bei idealer PM $57.3°$) und für $η = 0.5$ ergibt sich $ϕ_{max} = 26.6°$ (ideale PM: $28.7°$).
4.Es gilt nicht arctan$(η · cos(γ)) = η · cos(γ)$. Das heißt, dass das Sinkensignal im Gegensatz zum Quellensignal nicht cosinusförmig verläuft. Dies weist auf $\underline{nichtlineare Verzerrungen}$ hin ⇒ $\underline{Vorschlag 3}$.
5. Mit $γ = η · cos(ω_N · t)$ und $arctan(γ) ≈ γ – γ^3/3$ erhält man
$$ \phi(t) = \eta \cdot \cos (\omega_{\rm N} \cdot t) - \frac{\eta^3}{3}\cdot \cos^3 (\omega_{\rm N} \cdot t))=$$
$$ = \eta \cdot \cos (\omega_{\rm N} \cdot t) - \frac{\eta^3}{3}\cdot \left [ \frac{3}{4}\cdot \cos (\omega_{\rm N} \cdot t) + \frac{1}{4}\cdot \cos (3 \omega_{\rm N} \cdot t)\right ] =$$
$$ = \left(\eta - \frac{\eta^3}{4} \right) \cdot \cos (\omega_{\rm N} \cdot t) - \frac{\eta^3}{12}\cdot \cos (3\omega_{\rm N} \cdot t)) \hspace{0.05cm}.$$
Das bedeutet: Bei Verwendung der angegebenen Reihenentwicklung (Terme 5. und höherer Ordnung werden vernachlässigt) ist nur der Klirrfaktor dritter Ordnung von 0 verschieden. Man erhält:
$$K = K_3 = \frac{\eta^3/12}{\eta-\eta^3/4}= \frac{1}{12/\eta^2 -3} \hspace{0.05cm}.$$
Für $η = 1$ ergibt sich der Zahlenwert $K = 1/9 ≈ 11.1%$. Für $η = 0.5$ ist der Klirrfaktor $K = 1/45 ≈ 2.2%$.
Eine Simulation zeigt, dass man durch den Abbruch der Reihe nach dem Term dritter Ordnung einen Fehler macht, der den Klirrfaktor als zu hoch erscheinen lässt. Die per Simulation gewonnenen Werte sind $K ≈ 6%$ (für $η = 1$) und $K ≈ 2%$ (für $η = 0.5$). Der Fehler nimmt also mit wachsendem η mehr als proportional zu.