Difference between revisions of "Aufgaben:Exercise 3.7: PN Modulation"
From LNTwww
m (Javier moved page Exercises:Exercise 3.7: PN Modulation to Exercise 3.7: PN Modulation: Text replacement - "Exercises:Exercise" to "Aufgaben:Exercise") |
|||
| Line 3: | Line 3: | ||
}} | }} | ||
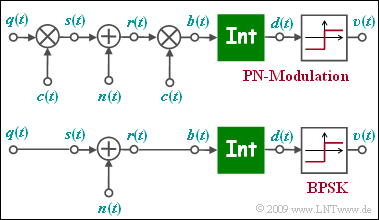
| − | [[File:P_ID2259__Mod_Z_5_2.png|right|frame| | + | [[File:P_ID2259__Mod_Z_5_2.png|right|frame|equivalent circuit diagrams of „PN modulation” and „BPSK”]] |
| − | + | The upper figure shows the equivalent circuit diagram of PN modulation ( ''Direct Sequence Spread Spectrum'', abbreviated DS-SS) in the equivalent low-pass range, where„ $n(t)$ stands for AWGN noise. | |
| − | + | Below, the low-pass model of binary phase modulation (BPSK) is sketched | |
| − | + | *The low-pass transmit signal $s(t)$ is equal to the rectangular source signal $q(t) ∈ \{+1, -1\}$ with rectangular duration $T$ only for reasons of uniformity. | |
| − | * | + | *The function of the integrator can be written as follows: |
| − | * | ||
:$$d (\nu T) = \frac{1}{T} \cdot \int_{(\nu -1 )T }^{\nu T} \hspace{-0.03cm} b (t )\hspace{0.1cm} {\rm d}t \hspace{0.05cm}.$$ | :$$d (\nu T) = \frac{1}{T} \cdot \int_{(\nu -1 )T }^{\nu T} \hspace{-0.03cm} b (t )\hspace{0.1cm} {\rm d}t \hspace{0.05cm}.$$ | ||
| − | * | + | *The two models differ in the multiplication by the $±1$-spreading signal $c(t)$ at the transmitter and receiver, whereas of this signal $c(t)$ only the spread degree $J$ is known. |
| − | * | + | *The specification of the specific spreading sequence (M sequence or Walsh function) is not important for the solution of this task. |
| − | + | It has to be examined whether the lower BPSK model can also be applied with PN modulation and whether the BPSK error probability | |
:$$p_{\rm B} = {\rm Q} \left( \hspace{-0.05cm} \sqrt { {2 \cdot E_{\rm B}}/{N_{\rm 0}} } \hspace{0.05cm} \right )$$ | :$$p_{\rm B} = {\rm Q} \left( \hspace{-0.05cm} \sqrt { {2 \cdot E_{\rm B}}/{N_{\rm 0}} } \hspace{0.05cm} \right )$$ | ||
| − | + | is also valid for PN modulation, or how the specified equation should be modified. | |
| Line 25: | Line 24: | ||
| − | '' | + | ''Notes:'' |
| − | * | + | *This exercise belongs to the chapter [[Mobile_Kommunikation/Die_Charakteristika_von_UMTS|Die Charakteristika von UMTS]]. |
| − | * | + | *The CDMA method used for UMTS is also known as "PN modulation". |
| − | * | + | *The nomenclature used in this task is also partly based on the [[Modulationsverfahren/PN–Modulation|PN–Modulation]] im Buch „Modulationsverfahren”. |
| − | === | + | ===Questionnaier=== |
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Which detection values are possible with BPSK (without noise)? |
|type="[]"} | |type="[]"} | ||
| − | - $d(\nu T)$ | + | - $d(\nu T)$ is gauss distributed. |
| − | - $d(\nu T)$ | + | - $d(\nu T)$ can take the values $+1$, $0$ und $-1$ . |
| − | + | + | + Only the values $d(\nu T) = +1$ und $d(\nu T) = -1$ are possible. |
| − | { | + | {Which values are possible with PN modulation in a noise-free case?? |
|type="[]"} | |type="[]"} | ||
| − | - $d(\nu T)$ | + | - $d(\nu T)$ is gauss distributed. |
| − | - $d(\nu T)$ | + | - $d(\nu T)$ can take the values $+1$, $0$ und $-1$ . |
| − | + | + | + Only the values $d(\nu T) = +1$ und $d(\nu T) = -1$ are possible. |
| − | { | + | {What modification must be made to the BPSK model so that it can also be used for PN modulation? |
|type="[]"} | |type="[]"} | ||
| − | + | + | + The noise $n(t)$ must be replaced by $n\hspace{0.05cm}'(t) = n(t) \cdot c(t)$ . |
| − | - | + | - The integration must now be done via $J \cdot T$ . |
| − | - | + | - The noise power must be reduced by the factor $J$ . |
| − | { | + | {The following applies $10 \cdot {\rm lg}\ (E_{\rm B}/N_0) = 6 \ \rm dB$. what error probability nbsp; $p_{\rm B}$ results with PN modulation? <br>''Hint'': For BPSK, the result is $p_{\rm B} \approx 2.3 \cdot 10^{-3}$. |
|type="[]"} | |type="[]"} | ||
| − | - | + | - The larger $J$ is selected, the smaller $p_{\rm B}$ is. |
| − | - | + | - The larger $J$ is selected, the larger $p_{\rm B}$. |
| − | + | + | + It results independently from $J$ , always the value $p_{\rm B} = 2.3 \cdot 10^{-3}$ results. |
</quiz> | </quiz> | ||
Revision as of 16:20, 2 July 2020
The upper figure shows the equivalent circuit diagram of PN modulation ( Direct Sequence Spread Spectrum, abbreviated DS-SS) in the equivalent low-pass range, where„ $n(t)$ stands for AWGN noise. Below, the low-pass model of binary phase modulation (BPSK) is sketched
- The low-pass transmit signal $s(t)$ is equal to the rectangular source signal $q(t) ∈ \{+1, -1\}$ with rectangular duration $T$ only for reasons of uniformity.
- The function of the integrator can be written as follows:
- $$d (\nu T) = \frac{1}{T} \cdot \int_{(\nu -1 )T }^{\nu T} \hspace{-0.03cm} b (t )\hspace{0.1cm} {\rm d}t \hspace{0.05cm}.$$
- The two models differ in the multiplication by the $±1$-spreading signal $c(t)$ at the transmitter and receiver, whereas of this signal $c(t)$ only the spread degree $J$ is known.
- The specification of the specific spreading sequence (M sequence or Walsh function) is not important for the solution of this task.
It has to be examined whether the lower BPSK model can also be applied with PN modulation and whether the BPSK error probability
- $$p_{\rm B} = {\rm Q} \left( \hspace{-0.05cm} \sqrt { {2 \cdot E_{\rm B}}/{N_{\rm 0}} } \hspace{0.05cm} \right )$$
is also valid for PN modulation, or how the specified equation should be modified.
Notes:
- This exercise belongs to the chapter Die Charakteristika von UMTS.
- The CDMA method used for UMTS is also known as "PN modulation".
- The nomenclature used in this task is also partly based on the PN–Modulation im Buch „Modulationsverfahren”.
Questionnaier
Musterlösung
(1) Richtig ist der Lösungsvorschlag 3:
- Es handelt sich hier um einen optimalen Empfänger.
- Ohne Rauschen ist das Signal $b(t)$ innerhalb eines jeden Bits konstant gleich $+1$ oder $-1$.
- Aus der angegebenen Gleichung für den Integrator
- $$d (\nu T) = \frac{1}{T} \cdot \hspace{-0.03cm} \int_{(\nu -1 )T }^{\nu T} \hspace{-0.3cm} b (t )\hspace{0.1cm} {\rm d}t$$
- folgt, dass $d(\nu T)$ nur die Werte $±1$ annehmen kann.
(2) Richtig ist wieder der Lösungsvorschlag 3:
- Im rauschfreien Fall ⇒ $n(t) = 0$ kann auf die zweifache Multiplikation mit $c(t) ∈ \{+1, -1\}$ ⇒ $c(t)^{2} = 1$ verzichtet werden, so dass das obere Modell mit dem unteren Modell identisch ist.
(3) Zutreffend ist der Lösungsvorschlag 1:
- Da beide Modelle im rauschfreien Fall identisch sind, muss nur das Rauschsignal angepasst werden: $n'(t) = n(t) \cdot c(t)$.
- Die Lösungsvorschläge 2 und 3 sind dagegen nicht zutreffend: Die Integration muss auch weiterhin über $T = J \cdot T_{c}$ erfolgen (nicht über $J \cdot T$) und die PN–Modulation verringert das AWGN–Rauschen nicht.
(4) Richtig ist der Lösungsvorschlag 3:
- Die für BPSK und AWGN–Kanal gültige Gleichung
- $$p_{\rm B} = {\rm Q} \left( \hspace{-0.05cm} \sqrt { \frac{2 \cdot E_{\rm B}}{N_{\rm 0}} } \hspace{0.05cm} \right )$$
- ist somit auch bei der PN–Modulation anwendbar und zwar unabhängig vom Spreizfaktor $J$ und von der spezifischen Spreizfolge.
- Bei AWGN–Rauschen wird die Fehlerwahrscheinlichkeit durch Bandspreizung weder vergrößert noch verkleinert.