Aufgaben:Exercise 1.6Z: Two Optimal Systems

• Return to book

Optimalsysteme im
Zeit- und Frequenzbereich

Betrachtet werden zwei binäre Übertragungssysteme  $\rm A$  und  $\rm B$ , die bei einem AWGN–Kanal mit Rauschleistungsdichte  $N_{0}$  das gleiche Fehlerverhalten aufweisen. In beiden Fällen gilt für die Bitfehlerwahrscheinlichkeit:

$$p_{\rm B} = {\rm Q} \left( \sqrt{{2 \cdot E_{\rm B}}/{N_0}}\right)\hspace{0.05cm}.$$

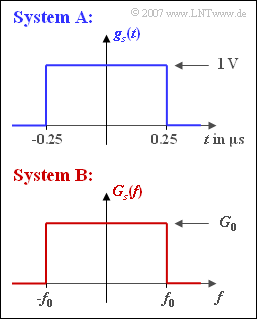
• Das System  $\rm A$  verwendet den NRZ–Sendegrundimpuls  $g_{s}(t)$  gemäß der oberen Skizze mit der Amplitude  $s_{0} = 1 \ \rm V$  und der Dauer  $T = 0.5\ \rm µ s$.
• Dagegen besitzt das System  $\rm B$ , das mit der gleichen Bitrate wie das System  $\rm A$  arbeiten soll, ein rechteckförmiges Sendegrundimpulsspektrum:

$$G_s(f) = \left\{ \begin{array}{c} G_0 \\ 0 \\ \end{array} \right.\quad \begin{array}{*{1}c} {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ \end{array}\begin{array}{*{20}c} |f| < f_0 \hspace{0.05cm}, \\ |f| > f_0 \hspace{0.05cm}.\\ \end{array}$$

Hinweise:

• Die Aufgabe gehört zum Kapitel  Optimierung der Basisbandübertragungssysteme.

• Beachten Sie bitte, dass hier die Impulsamplitude in „Volt” angegeben ist, so dass die mittlere Energie pro Bit  $(E_{\rm B})$  die Einheit  $\rm V^{2}/Hz$  aufweist.

Fragebogen

1

Mit welcher Bitrate arbeiten die beiden Systeme?

$R \ = \ $ $\ \rm Mbit/s$

2

Berechnen Sie die Energie pro Bit für das System  $\rm A$.

$E_{\rm B} \ = \ $ $\ \cdot 10^{-6} \ \rm V^{2}/Hz$

3

Welche Aussagen gelten für die Empfangsfilter der Systeme  $\rm A$  und  $\rm B$?

	Bei System  $\rm A$  hat  $H_{\rm E}(f)$  einen si–förmigen Verlauf.
	Bei System  $\rm B$  ist  $H_{\rm E}(f)$  ein idealer, rechteckförmiger Tiefpass.
	$H_{\rm E}(f)$  lässt sich bei System  $\rm B$  durch einen Integrator realisieren.

4

Für welche Grenzfrequenz  $f_{0}$  weist das System  $\rm B$  die Symboldauer  $T$  auf?

$f_{0} \ = \ $ $\ \rm MHz$

5

Wie groß ist die konstante Höhe  $G_{0}$  des Spektrums von  $\rm B$  zu wählen, damit sich die gleiche Energie pro Bit ergibt wie bei System  $\rm A$?

$G_{0} \ = \ $ $\ \cdot 10^{-6} \ \rm V/Hz$

6

Wäre eines der beiden Systeme auch bei Spitzenwertbegrenzung geeignet?

	System  $\rm A$,
	System  $\rm B$.

Musterlösung

Solution

(1)  Beide Systeme arbeiten gemäß der Angabe mit gleicher Bitrate.

• Der NRZ–Sendegrundimpuls von System A hat die Symboldauer $T = 0.5\ \rm µ s$.
• Daraus ergibt sich für die Bitrate $R = 1/T$ $\underline{= 2\ \rm Mbit/s}$.

(2)  Die Energie des NRZ–Sendegrundimpulses von System A ergibt sich zu

$$E_{\rm B} = \int_{-\infty}^{+\infty}g_s^2 (t)\,{\rm d} t = s_0^2 \cdot T = {1\,{\rm V^2}}\cdot {0.5 \cdot 10^{-6}\,{\rm s}}\hspace{0.1cm}\underline { = 0.5 \cdot 10^{-6}\,{\rm V^2/Hz}}\hspace{0.05cm}.$$

(3)  Die beiden ersten Aussagen treffen zu:

• In beiden Fällen muss $h_{\rm E}(t)$ formgleich mit $g_{s}(t)$ und $H_{\rm E}(f)$ formgleich mit $G_{s}(f)$ sein.
• Somit ergibt sich beim System A eine rechteckförmige Impulsantwort $h_{\rm E}(t)$ und damit ein si–förmiger Frquenzgang $H_{\rm E}(f)$.
• Beim System B ist $H_{\rm E}(f)$ wie $G_{s}(f)$ rechteckförmig und damit die Impulsantwort $h_{\rm E}(t)$ eine si–Funktion.
• Aussage 3 ist falsch:   Ein Integrator besitzt eine rechteckige Impulsantwort und würde sich für die Realisierung von System A anbieten, nicht jedoch für System B.

(4)  Beim System B stimmt $G_{d}(f)$ mit $G_{s}(f)$ nahezu überein.

• Lediglich bei der Nyquistfrequenz gibt es einen Unterschied, der sich aber für die hier angestellten Betrachtungen nicht weiter auswirkt:
• Während $G_{s}(f_{\rm Nyq}) = 1/2$ gilt, ist $G_{d}(f_{\rm Nyq}) = 1/4$.

• Es ergibt sich also ein Nyquistsystem mit Rolloff–Faktor $r = 0$.
• Daraus folgt für die Nyquistfrequenz aus der Bedingung, dass die Symboldauer ebenfalls $T = 0.5\ \rm µ s$ sein soll:

$$f_{\rm 0} = f_{\rm Nyq} = \frac{1 } {2 \cdot T} = \frac{1 } {2 \cdot 0.5 \cdot 10^{-6}\,{\rm s}}\hspace{0.1cm}\underline {= 1\,{\rm MHz}}\hspace{0.05cm}.$$

(5)  Für die Energie des Sendegrundimpulses kann auch geschrieben werden:

$$E_{\rm B} = \int_{-\infty}^{+\infty}|G_s(f)|^2 \,{\rm d} f = G_0^2 \cdot 2 f_0\hspace{0.05cm}.$$

• Mit den Ergebnissen aus (2) und (4) folgt daraus:

$$G_0^2 = \frac{E_{\rm B}}{2 f_0} = \frac{5 \cdot 10^{-7}\,{\rm V^2/Hz}}{2 \cdot 10^{6}\,{\rm Hz}}= 2.5 \cdot 10^{-13}\,{\rm V^2/Hz^2} \hspace{0.3cm}\Rightarrow \hspace{0.3cm}G_0 \hspace{0.1cm}\underline {= 0.5 \cdot 10^{-6}\,{\rm V/Hz}} \hspace{0.05cm}.$$

(6)  Richtig ist der Lösungsvorschlag 1:

• Das System A stellt auch bei Spitzenwertbegrenzung das optimale System dar.
• Dagegen wäre das System B aufgrund des äußerst ungünstigen Crestfaktors hierfür denkbar ungeeignet.