Aufgaben:Exercise 3.3Z: GSM 900 and GSM 1800

• Return to book

$\rm GSM \ 900$  und  $\rm GSM \ 1800$

Der seit $1992$ in Europa etablierte Mobilfunkstandard  $\rm GSM$  (Global System for Mobile Communications)  nutzt Frequenz– und Zeitmultiplex, um mehreren Nutzern die Kommunikation in einer Zelle zu ermöglichen.

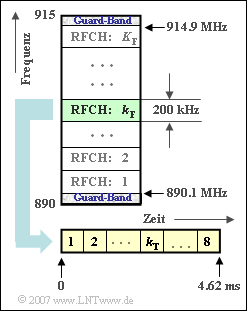
Im Folgenden sind wichtige Kenngrößen des in der Grafik dargestellten Systems  $\rm GSM \ 900$  in etwas vereinfachter Form angegeben.

• Das Frequenzband des Uplinks (die Verbindung von der Mobil– zur Basisstation) liegt zwischen  $890\ \rm MHz$  und  $915 \ \rm MHz$.
• Unter Berücksichtigung der Guard–Bänder an den beiden Enden steht somit für den Uplink eine Gesamtbandbreite von  $24.8 \ \rm MHz$ zur Verfügung.
• Dieses Band wird von insgesamt  $K_{\rm F}$  Teilkanälen (Radio Frequency Channels) genutzt, die mit jeweiligem Frequenzabstand  $200 \ \rm kHz$  nebeneinander liegen. Die Nummerierung geschieht mit der Laufvariablen  $k_{\rm F}$.
• Der Frequenzbereich für den Downlink (die Verbindung von der Basis– zur Mobilstation) liegt um den Duplexabstand  $45 \ \rm MHz$  oberhalb des Uplinks und ist ansonsten in gleicher Weise wie dieser aufgebaut.
• Jeder dieser FDMA–Teilkanäle wird gleichzeitig von  $K_{\rm T} = 8$  Teilnehmern im Zeitmultiplex  (Time Division Multiple Access, TDMA) genutzt.

Das System GSM $1800$ ist in ähnlicher Weise aufgebaut, jedoch mit folgenden Unterschieden:

• Der Frequenzbereich des Uplinks liegt zwischen  $1710 \ \rm MHz$  und  $1785 \ \rm MHz$.
• Der Duplexabstand beträgt  $95 \ \rm MHz$.

Hinweise:

• Diese Aufgabe gehört zum Kapitel  Funkschnittstelle.
• Bezug genommen wird insbesondere auf die Seite  Realisierung von FDMA und TDMA

Fragebogen

1

Wieviele Teilkanäle entstehen beim  $\rm GSM \ 900$  durch Frequenzmultiplex?

$K_{\rm F} \ = \ $

2

Wieviele Frequenzkanäle gibt es beim  $\rm GSM \ 1800$?

$K_{\rm F} \ = \ $

3

Welche Mittenfrequenz benutzt der Frequenzkanal mit der Nummer  $k_{\rm F} = 200$  im Downlink des  $\rm GSM \ 1800$?

$f_{\rm M} \ = \ $ $ \ \rm MHz$

4

Wieviele Teilnehmer  $K$  können beim  $\rm GSM \ 1800$  gleichzeitig aktiv sein?

$K \ = \ $

Musterlösung

Solution

(1)  Aus der Gesamtbandbreite von $25 \ {\rm MHz}\ (800 \text{...} 915 \ \rm MHz)$, den beiden Schutzbereichen von je $100 \ \rm kHz$ an den Rändern und dem Kanalabstand $200 \ \rm kHz$ ergibt sich für das $\rm GSM \ 900$:

$$K_{\rm F} = \frac{ 914.9 \,{\rm MHz}- 890.1 \,{\rm MHz}}{0.2 \,{\rm MHz}} \hspace{0.15cm} \underline {= 124}\hspace{0.05cm}.$$

(2)  Beim $\rm GSM \ 1800$ steht nun in jeder Richtung eine Bandbreite von $75 \ \rm MHz$ zur Verfügung.

• Unter Berücksichtigung der beiden Schutzbänder und des gleichen Kanalabstandes $200 \ \rm kHz$ erhält man hier:

$$K_{\rm F} = \frac{ 75 \,{\rm MHz}- 0.2 \,{\rm MHz}}{0.2 \,{\rm MHz}} \hspace{0.15cm} \underline {= 374}\hspace{0.05cm}.$$

(3)  Beim $\rm GSM \ 1800$ beginnt der Uplink bei $1710 \ \rm MHz$ und der Downlink bei

$$1710 \,{\rm MHz}\,\,({\rm Uplink})+ 95 \,{\rm MHz}\,\,({\rm Duplexabstand}) ={1805 \,{\rm MHz}} \hspace{0.05cm}.$$

• Der erste Downlink–Kanal $(k_{\rm F} = 1)$ liegt um die Mittenfrequenz $f_{\rm M} = 1805.2 \ \rm MHz$ höher,
• der Kanal mit der Nummer $k_{\rm F} = 200$ um den Frequenzabstand $199 \cdot 0.2 \ \rm MHz$:

$$f_{\rm M} (k_{\rm F} = 200) \hspace{0.15cm} \underline { = {1845 \,{\rm MHz}}} \hspace{0.05cm}.$$

(4)  Mit dem Ergebnis der Teilaufgabe (2) und $K_{\rm T} = 8$ erhält man:

$$K ({\rm GSM \hspace{0.15cm}1800}) = 374 \cdot 8 \hspace{0.15cm} \underline { = 2992}\hspace{0.05cm}.$$