Difference between revisions of "Aufgaben:Exercise 4.10: Turbo Encoder for UMTS and LTE"
m (Text replacement - "Mobile_Kommunikation/" to "Mobile_Communications/") |
m (Text replacement - "[[Kanalcodierung" to "[[Channel_Coding") |
||
| Line 2: | Line 2: | ||
[[File:P_ID3051__KC_A_4_10_v1.png|right|frame|Turbocoder für UMTS und LTE]] | [[File:P_ID3051__KC_A_4_10_v1.png|right|frame|Turbocoder für UMTS und LTE]] | ||
| − | Die Mobilfunkstandards [[Mobile_Communications/Die_Charakteristika_von_UMTS|UMTS]] und [[Mobile_Communications/Allgemeines_zum_Mobilfunkstandard_LTE|LTE]] verwenden jeweils einen Turbocode, der weitgehend identisch ist mit dem im Kapitel [[ | + | Die Mobilfunkstandards [[Mobile_Communications/Die_Charakteristika_von_UMTS|UMTS]] und [[Mobile_Communications/Allgemeines_zum_Mobilfunkstandard_LTE|LTE]] verwenden jeweils einen Turbocode, der weitgehend identisch ist mit dem im Kapitel [[Channel_Coding/Grundlegendes_zu_den_Turbocodes|Grundlegendes zu den Turbocodes]] beschriebenen Coder. |
* Der $1/n$–Faltungscode ist systematisch, das heißt, dass die Codesequenz $\underline{x}$ die Informationssequenz $\underline{u}$ als Komponente beinhaltet. | * Der $1/n$–Faltungscode ist systematisch, das heißt, dass die Codesequenz $\underline{x}$ die Informationssequenz $\underline{u}$ als Komponente beinhaltet. | ||
* Die Paritysequenzen $\underline{p}_1$ und $\underline{p}_2$ basieren auf der gleichen Übertragungsfunktion: | * Die Paritysequenzen $\underline{p}_1$ und $\underline{p}_2$ basieren auf der gleichen Übertragungsfunktion: | ||
| Line 15: | Line 15: | ||
''Hinweise:'' | ''Hinweise:'' | ||
| − | * Die Aufgabe gehört zum Kapitel [[ | + | * Die Aufgabe gehört zum Kapitel [[Channel_Coding/Grundlegendes_zu_den_Turbocodes| Grundlegendes zu den Turbocodes]]. |
* Erwartet werden Kenntnisse über | * Erwartet werden Kenntnisse über | ||
| − | ** die [[ | + | ** die [[Channel_Coding/Algebraische_und_polynomische_Beschreibung|algebraische und polynomische Beschreibung von Faltungscodes]], |
| − | ** die [[ | + | ** die [[Channel_Coding/Codebeschreibung_mit_Zustands%E2%80%93_und_Trellisdiagramm|Coderbeschreibung mit Zustands– und Trellisdiagramm]]. |
* Weitere Hinweise zur Vorgehensweise finden Sie in der [[Aufgaben:4.08_Wiederholung_zu_den_Faltungscodes|Aufgabe 4.8]] und der [[Aufgaben:Aufgabe_4.09:_Recursive_Systematic_Convolutional_Codes|Aufgabe 4.9]]. | * Weitere Hinweise zur Vorgehensweise finden Sie in der [[Aufgaben:4.08_Wiederholung_zu_den_Faltungscodes|Aufgabe 4.8]] und der [[Aufgaben:Aufgabe_4.09:_Recursive_Systematic_Convolutional_Codes|Aufgabe 4.9]]. | ||
* Die Informationssequenz $\underline{u}$ wird zur einfacheren Beschreibung in den Teilaufgaben teilweise durch deren $D$–Transformierte angegeben. Beispielsweise gilt: | * Die Informationssequenz $\underline{u}$ wird zur einfacheren Beschreibung in den Teilaufgaben teilweise durch deren $D$–Transformierte angegeben. Beispielsweise gilt: | ||
| Line 77: | Line 77: | ||
| − | '''(2)''' Wie der Vergleich des [[ | + | '''(2)''' Wie der Vergleich des [[Channel_Coding/Algebraische_und_polynomische_Beschreibung#Filterstruktur_bei_gebrochen.E2.80.93rationaler_.C3.9Cbertragungsfunktion|rekursiven Filters]] auf der Angabenseite mit der [[Aufgaben:4.10_UMTS/LTE%E2%80%93Turbocoder|Filterstruktur]] im Theorieteil für gebrochen–rationales $G(D)$ zeigt, ist der <u>Lösungsvorschlag 1</u> richtig. |
| Line 154: | Line 154: | ||
''Weitergehende Hinweise:'' | ''Weitergehende Hinweise:'' | ||
* Für einen Turbocode sind insbesondere solche Eingangsfolgen $\underline{u}$, deren $D$–Transformierte als $U(D) = f(D) \cdot [1 + D^{P}]$ darstellbar sind, äußerst ungünstig. | * Für einen Turbocode sind insbesondere solche Eingangsfolgen $\underline{u}$, deren $D$–Transformierte als $U(D) = f(D) \cdot [1 + D^{P}]$ darstellbar sind, äußerst ungünstig. | ||
| − | *Sie bewirken den <i>Error Floor</i>, wie er auf der Seite [[ | + | *Sie bewirken den <i>Error Floor</i>, wie er auf der Seite [[Channel_Coding/Grundlegendes_zu_den_Turbocodes#Leistungsf.C3.A4higkeit_der_Turbocodes|Leistungsfähigkeit der Turbocodes]] im Theorieteil zu erkennen ist. |
*$P$ gibt dabei die Periode der Impulsantwort $\underline{g}$ an. | *$P$ gibt dabei die Periode der Impulsantwort $\underline{g}$ an. | ||
*In unserem Beispiel gilt $f(D) = D$ und $P = 7$. | *In unserem Beispiel gilt $f(D) = D$ und $P = 7$. | ||
Revision as of 13:51, 9 July 2020
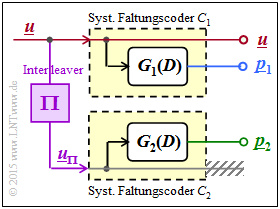
Die Mobilfunkstandards UMTS und LTE verwenden jeweils einen Turbocode, der weitgehend identisch ist mit dem im Kapitel Grundlegendes zu den Turbocodes beschriebenen Coder.
- Der $1/n$–Faltungscode ist systematisch, das heißt, dass die Codesequenz $\underline{x}$ die Informationssequenz $\underline{u}$ als Komponente beinhaltet.
- Die Paritysequenzen $\underline{p}_1$ und $\underline{p}_2$ basieren auf der gleichen Übertragungsfunktion:
- $$G_1(D) = G_2(D) = G(D).$$
- $\underline{p}_1$ und $\underline{p}_2$ verwenden allerdings unterschiedliche Eingangssequenzen $\underline{u}$ bzw. $\underline{u}_{\pi}$. Hierbei kennzeichnet ${\rm \Pi}$ den Interleaver, bei UMTS und LTE meist ein $S$–Random–Interleaver.
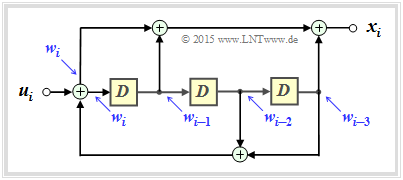
Der wesentliche Unterschied gegenüber der Beschreibung im Theorieteil ergibt sich durch eine andere Übertragungsfunktion $G(D)$, die durch die links gezeichnete rekursive Filterstruktur gegeben ist.
Hinweise:
- Die Aufgabe gehört zum Kapitel Grundlegendes zu den Turbocodes.
- Erwartet werden Kenntnisse über
- Weitere Hinweise zur Vorgehensweise finden Sie in der Aufgabe 4.8 und der Aufgabe 4.9.
- Die Informationssequenz $\underline{u}$ wird zur einfacheren Beschreibung in den Teilaufgaben teilweise durch deren $D$–Transformierte angegeben. Beispielsweise gilt:
- $$\underline{u}= (\hspace{0.05cm}0\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm}0\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm}\hspace{0.05cm} \text{...}\hspace{0.05cm}) \quad \circ\!\!-\!\!\!-^{\hspace{-0.25cm}D}\!\!\!-\!\!\bullet\quad U(D) = D+ D^2\hspace{0.05cm},$$
- $$\underline{u}= (\hspace{0.05cm}0\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm}0\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm}\hspace{0.05cm} \text{...}\hspace{0.05cm}) \quad \circ\!\!-\!\!\!-^{\hspace{-0.25cm}D}\!\!\!-\!\!\bullet\quad U(D) = D+ D^8\hspace{0.05cm}.$$
Fragebogen
Musterlösung
(1) Die Codeparameter sind $k = 1$ und $n = 3$ ⇒ Coderate $\underline{R = 1/3}$.
- Das Gedächtnis (englisch: Memory) ist $\underline{m = 3}$.
- Die Einflusslängen ergeben sich zu $\nu = 1, \ \nu_2 = 4$ und $\nu_3 = 4$ ⇒ Gesamteinflusslänge $\underline{\nu = 9}$.
(2) Wie der Vergleich des rekursiven Filters auf der Angabenseite mit der Filterstruktur im Theorieteil für gebrochen–rationales $G(D)$ zeigt, ist der Lösungsvorschlag 1 richtig.
(3) Richtig sind die Lösungsvorschläge 2 und 3:
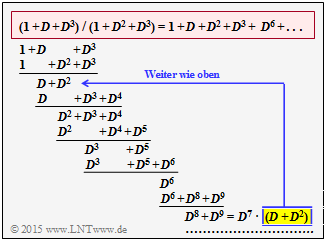
Die obere Grafik verdeutlicht die Polynomdivision $(1 + D + D^3) \ / \ (1 + D^2 + D^3)$. Zur Erläuterung:
- Abgebrochen ist die Darstellung mit dem Rest $D^8 + D^9 = D^7 \cdot (D + D^2)$.
- Damit gilt auch:
- $$(D^8 + D^9) \hspace{0.05cm} /\hspace{0.05cm} (1+ D^2+ D^3 ) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} D^7 \cdot (D+ D^2+ D^3 + D^6) + {\rm Rest_2}$$
- Nach Zusammenfassen:
- $$G(D) = 1 + D + D^2 + D^3 + D^6 + D^8+ D^9+ D^{10} + D^{13} + \hspace{0.05cm}\text{ ... }\hspace{0.05cm} \hspace{0.05cm}. $$
- Die $D$–Rücktransformierte ergibt den Lösungsvorschlag 2:
- $$\underline{g}= (\hspace{0.05cm}1\hspace{0.05cm}, \hspace{0.05cm} 1\hspace{0.05cm}, \hspace{0.05cm} 1\hspace{0.05cm}, \hspace{0.05cm} 1\hspace{0.05cm}, \hspace{0.05cm} 0\hspace{0.05cm}, \hspace{0.05cm} 0\hspace{0.05cm}, \hspace{0.05cm} 1\hspace{0.05cm}, \hspace{0.05cm} 0\hspace{0.05cm}, \hspace{0.05cm} 1\hspace{0.05cm}, \hspace{0.05cm} 1\hspace{0.05cm}, \hspace{0.05cm} 1\hspace{0.05cm}, \hspace{0.05cm} 0\hspace{0.05cm}, \hspace{0.05cm} 0\hspace{0.05cm}, \hspace{0.05cm} 1\hspace{0.05cm}, \hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm}\text{ ... }\hspace{0.05cm})\hspace{0.05cm}. $$
- Die Impulsantwort setzt sich bis ins Unendliche fort ⇒ Lösungsvorschlag 3 ist ebenfalls richtig.
(4) Die Impulsantwort kann wie folgt ausgedrückt werden:
- $$\underline{g}= \Big (\hspace{0.03cm}1\hspace{0.03cm}, \big [ \hspace{0.03cm} 1\hspace{0.03cm}, \hspace{0.03cm} 1\hspace{0.03cm}, \hspace{0.03cm} 1\hspace{0.03cm}, \hspace{0.03cm} 0\hspace{0.03cm}, \hspace{0.03cm} 0\hspace{0.03cm}, \hspace{0.03cm} 1\hspace{0.03cm}, \hspace{0.03cm} 0\hspace{0.03cm} \big ]_{\rm per} \Big ) \hspace{0.15cm}\Rightarrow \hspace{0.15cm} \underline{P = 7} \hspace{0.05cm}. $$
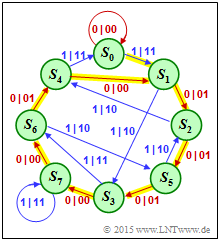
Im Zustandsübergangsdiagramm (rechts) ist die Impulsantwort $\underline{g}$ gelb hinterlegt. Die Impulsantwort ergibt sich als die Paritysequenz $\underline{p}$ für die Informationssequenz $\underline{u} = (1, \, 0, \, 0, \, 0, \, 0, \, \text{ ... })$.
- Die Übergänge im Diagramm sind mit „$u_i\hspace{0.05cm}|\hspace{0.05cm}\underline{x}_i$” beschriftet, was gleichbedeutend ist mit „$u_i\hspace{0.05cm}|\hspace{0.05cm}u_i \hspace{0.05cm}p_i$”.
- Die Paritysequenz $\underline{p} \ (=$ Impulsantwort $\underline{g})$ ergibt sich somit aus dem jeweiligen zweiten Coderausgangssymbol.
- $\underline{g}$ wird durch folgende Zustände repräsentiert:
- $$S_0 → [S_1 → S_2 → S_5 → S_3 → S_7 → S_6 → S_4 ] → [S_1 → \ ... \ → S_4] → \ \text{ ... } $$
(5) Die folgende Grafik zeigt die Lösung anhand der Generatormatrix $\mathbf{G}$. Es gilt $\underline{u} = (0, \, 1, \, 1, \, 0, \, 0, \, \text{ ... } )$.
Man erkennt, dass die Lösungsvorschläge 1, 2 und 3 richtig sind:
- Die vorliegende Paritysequenz $\underline{p}$ hat die gleiche Periode $P = 7$ wie die Impulsantwort $\underline{g}$.
- Das Hamming–Gewicht der (begrenzten) Eingangsfolge ist tatsächlich $w_{\rm H}(\underline{u}) = 2$.
- Der Vorschlag 4 ist falsch. Vielmehr gilt hier für die semi–infinite Ausgangssequenz: $w_{\rm H}(\underline{p}) → \infty$.
Im Übergangsdiagramm werden zunächst die Zustände $S_0 → S_0 → S_1 → S_3 → S_7 → S_6 → S_4 → S_1$ durchlaufen. Danach folgt (unendlich oft) der periodische Anteil $S_1 → S_2 → S_5 → S_3 → S_7 → S_6 → S_4 → S_1$.
(6) Die letzte Grafik zeigt die Lösung für $U(D) = D + D^8 \Rightarrow \underline{u} = (0, \, 1, \, 0, \, 0, \, 0, \, 0, \, 0, \, 0, \, 1, \, 0, \, 0, \, \text{ ... })$.
Richtig sind die Lösungsvorschläge 3 und 4:
- Die Eingangssequenz $\underline{u}$ beinhaltet zwei Einsen und die Ausgangssequenz $\underline{p}$ sechs Einsen.
- Ab der Position 10 ist nun die Ausgangssequenz $\underline{p} \equiv\underline{0}$
⇒ die Vorschläge 1 und 2 treffen also nicht zu.
Weitergehende Hinweise:
- Für einen Turbocode sind insbesondere solche Eingangsfolgen $\underline{u}$, deren $D$–Transformierte als $U(D) = f(D) \cdot [1 + D^{P}]$ darstellbar sind, äußerst ungünstig.
- Sie bewirken den Error Floor, wie er auf der Seite Leistungsfähigkeit der Turbocodes im Theorieteil zu erkennen ist.
- $P$ gibt dabei die Periode der Impulsantwort $\underline{g}$ an.
- In unserem Beispiel gilt $f(D) = D$ und $P = 7$.