Difference between revisions of "Applets:Zweidimensionale Laplace-Zufallsgrößen (Applet)"
m (Text replacement - "[[Stochastische_Signaltheorie/" to "[[Theory_of_Stochastic_Signals/") |
m (Text replacement - "[[Biografien_und_Bibliografien" to "[[Biographies_and_Bibliographies") |
||
| Line 199: | Line 199: | ||
==Über die Autoren== | ==Über die Autoren== | ||
Dieses interaktive Berechnungstool wurde am [http://www.lnt.ei.tum.de/startseite Lehrstuhl für Nachrichtentechnik] der [https://www.tum.de/ Technischen Universität München] konzipiert und realisiert. | Dieses interaktive Berechnungstool wurde am [http://www.lnt.ei.tum.de/startseite Lehrstuhl für Nachrichtentechnik] der [https://www.tum.de/ Technischen Universität München] konzipiert und realisiert. | ||
| − | *Die erste Version wurde 2003 von [[ | + | *Die erste Version wurde 2003 von [[Biographies_and_Bibliographies/An_LNTwww_beteiligte_Studierende#Ji_Li_.28Bachelorarbeit_EI_2003.2C_Diplomarbeit_EI_2005.29|Ji Li]] im Rahmen ihrer Diplomarbeit mit „FlashMX–Actionscript” erstellt (Betreuer: [[Biographies_and_Bibliographies/An_LNTwww_beteiligte_Mitarbeiter_und_Dozenten#Prof._Dr.-Ing._habil._G.C3.BCnter_S.C3.B6der_.28am_LNT_seit_1974.29|Günter Söder]]). |
| − | * 2019 wurde das Programm von [[ | + | * 2019 wurde das Programm von [[Biographies_and_Bibliographies/An_LNTwww_beteiligte_Studierende#Carolin_Mirschina_.28Ingenieurspraxis_Math_2019.2C_danach_Werkstudentin.29|Carolin Mirschina]] im Rahmen einer Werkstudententätigkeit auf „HTML5” umgesetzt und neu gestaltet (Betreuer: [[Biographies_and_Bibliographies/Beteiligte_der_Professur_Leitungsgebundene_%C3%9Cbertragungstechnik#Tasn.C3.A1d_Kernetzky.2C_M.Sc._.28bei_L.C3.9CT_seit_2014.29|Tasnád Kernetzky]]). |
Revision as of 14:00, 9 July 2020
Contents
Programmbeschreibung
Das Applet verdeutlicht die Eigenschaften von mittelwertfreien laplaceverteilten Zufallsgrößen $X$ und $Y\hspace{-0.1cm}$, gekennzeichnet durch die beiden Parameter ${\it \lambda_X}$ und ${\it \lambda_Y}$. Es wird vorausgesetzt, dass $X$ und $Y\hspace{-0.1cm}$ statistisch unabhängig seien.
Eine solche Zufallsgröße approximiert zum Beispiel die Amplitudenverteilung eines Audiosignals (Sprache oder Musik). Die Kenntnis hierüber erlaubt die bestmögliche Digitalisierung (nichtlineare Quantisierung) eines solchen Signals.
Das Applet zeigt
- die zweidimensionale Wahrscheinlichkeitsdichtefunktion ⇒ $\rm 2D\hspace{-0.1cm}-\hspace{-0.1cm}WDF$ $f_{XY}(x, \hspace{0.1cm}y)$ in dreidimensionaler Darstellung sowie in Form von Höhenlinien,
- die zugehörige Randwahrscheinlichkeitsdichtefunktion ⇒ $\rm 1D\hspace{-0.1cm}-\hspace{-0.1cm}WDF$ $f_{X}(x)$ der Zufallsgröße $X$ als blaue Kurve; ebenso $f_{Y}(y)$ für die zweite Zufallsgröße,
- die zweidimensionale Verteilungsfunktion ⇒ $\rm 2D\hspace{-0.1cm}-\hspace{-0.1cm}VTF$ $F_{XY}(x, \hspace{0.1cm}y)$ als 3D-Plot,
- die Verteilungsfunktion ⇒ $\rm 1D\hspace{-0.1cm}-\hspace{-0.1cm}VTF$ $F_{X}(x)$ der Zufallsgröße $X$; ebenso $F_{Y}(y)$ als rote Kurve.
Das Applet verwendet das Framework Plot.ly
Einige Versuche, dass das „lambda” kursiv dargestellt wird: λ ${\it λ_X}$ $𝜆$ 𝜆
Theoretischer Hintergrund
Definition und Eigenschaften der Laplace–Verteilung
$(1)$ Für die Wahrscheinlichkeitsdichtefunktion (WDF, englisch: Probability Density Function, kurz: PDF) der laplaceverteilten Zufallsgröße $X$ gilt ⇒ $\rm 1D\hspace{-0.1cm}-\hspace{-0.1cm}WDF$:
- $$f_{X}(x)=\frac{\lambda_X} {2}\cdot{\rm e}^ { - \lambda_X \hspace{0.05cm} \cdot \hspace{0.05cm} \vert \hspace{0.05cm} x \hspace{0.05cm} \vert}.$$
$(2)$ Daraus folgt für die Verteilungsfunktion (VTF, englisch: Cumulative Distribution Function, kurz: CDF) ⇒ $\rm 1D\hspace{-0.1cm}-\hspace{-0.1cm}VTF$:
- $$F_{X}(x) = {\rm Pr}\big [X \le x \big ] = \int_{-\infty}^{x} f_{X}(\xi) \,\,{\rm d}\xi = 0.5 + 0.5 \cdot {\rm sign}(x) \cdot \big [ 1 - {\rm e}^ { - \lambda_X \hspace{0.05cm} \cdot \hspace{0.05cm} \vert \hspace{0.05cm} x \hspace{0.05cm} \vert}\big ] \hspace{0.5cm} \Rightarrow \hspace{0.5cm} F_{X}(-\infty) = 0, \hspace{0.2cm}F_{X}(0) = 0.5, \hspace{0.2cm} F_{X}(+\infty) = 1.$$
$(3)$ Alle Momente $m_k = {\rm E}\big [X^k \big ]$ mit ungeradzahligem $k$ sind Null (Begründung: Symmetrische WDF). Insbesondere gilt auch für den linearen Mittelwert: $m_1 = {\rm E}\big [X \big ] = 0$.
$(4)$ Für die Momente $m_k = {\rm E}\big [X^k \big ]$ mit geradzahligem $k$ gilt:
- $$m_k = \int_{-\infty}^{+\infty} x^k \cdot f_{X}(x) \,\,{\rm d} x = \frac{k!}{\lambda_X^k} \hspace{0.5cm} \Rightarrow \hspace{0.5cm} m_2 = \sigma^2 = \frac{2}{\lambda_X^2}.$$
$\text{Beispiel: Zusammenhang zwischen Exponentialverteilung und Laplaceverteilung}$
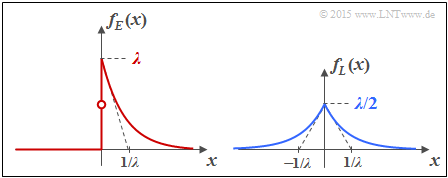
Wir betrachten die Wahrscheinlichkeitsdichtefunktionen (WDF) zweier wertkontinuierlicher Zufallsgrößen $E$ und $L$ mit gleichem WDF–Parameter $\lambda$:
- Die Zufallsgröße $E$ ist exponentialverteilt: Für $x<0$ ist $f_E(x) = 0$, und für positive $x$–Werte gilt:
- $$f_E(x) = \lambda \cdot {\rm e}^{-\lambda \hspace{0.05cm}\cdot \hspace{0.05cm}x}\hspace{0.05cm}. $$
- Für die laplaceverteilte Zufallsgröße $L$ gilt im gesamten Bereich$ - \infty < x < + \infty$:
- $$f_L(x) = \lambda/2 \cdot {\rm e}^{- \lambda \hspace{0.05cm}\cdot \hspace{0.05cm}\vert x \vert}\hspace{0.05cm}.$$
- Momente der Exponentialverteilung: $m_k = {k!}/{\lambda^k}$
⇒ linearer Mittelwert $m_1 = 1/{\lambda}$, quadratischer Mittelwert $m_2 = 2/{\lambda}^2$, Varianz $\sigma^2=m_2- m_1^2 = 1/{\lambda}^2$.
Wie aus der Grafik zu ersehen ist die Laplaceverteilung eine „zweiseitige Exponentialverteilung”. Daraus folgt:
- Für ungeradzahliges $k$ ergibt sich bei der Laplaceverteilung aufgrund der Symmetrie stets $m_k= 0$. Unter Anderem: Linearer Mittelwert $m_1 = 0$.
- Für geradzahliges $k$ stimmen die Momente von Exponentialverteilung und Laplaceverteilung überein. Unter Anderem: Quadratischer Mittelwert $m_2 = 2/{\lambda}^2$.
- Die Varianz der mittelwertfreien laplaceverteiten Zufallsgröße ist bei gleichem $\lambda$ doppelt so groß wie bei der Exponentialverteilung: $\sigma^2 = 2/\lambda^2$.
Zweidimensionale Wahrscheinlichkeitsdichtefunktion ⇒ 2D–WDF
Wir setzen voraus, dass zwischen den beiden Zufallsgrößen $X$ und $Y\hspace{-0.1cm}$ keine statistischen Abhängigkeiten bestehen. Für die Wahrscheinlichkeitsdichtefunktion der zweidimensionalen Zufallsgröße $XY$ an der Stelle $(x, y)$ gilt in diesem Fall:
- $$f_{XY}(x, \hspace{0.1cm}y) = f_{X}(x) \cdot f_{Y}(y). $$
Sind die Zufallsgrößen $X$ und $Y\hspace{-0.1cm}$ mittelwertfrei und laplaceverteilt, dann kann hierfür geschrieben werden:
- $$f_{XY}(x, \ y)=\frac{\lambda_X \cdot \lambda_Y} {4}\cdot{\rm e}^ { - \lambda_X \hspace{0.05cm} \cdot \hspace{0.05cm} \vert \hspace{0.05cm} x \hspace{0.05cm} \vert} \cdot {\rm e}^ { - \lambda_Y \hspace{0.05cm} \cdot \hspace{0.05cm} \vert \hspace{0.05cm} y \hspace{0.05cm} \vert}=\frac{\lambda_X \cdot \lambda_Y} {4}\cdot{\rm e}^ { - \hspace{0.05cm}\left (\lambda_X \hspace{0.05cm} \cdot \hspace{0.05cm} \vert \hspace{0.05cm} x \hspace{0.05cm} \vert+ \lambda_Y \hspace{0.05cm} \cdot \hspace{0.05cm} \vert \hspace{0.05cm} y \hspace{0.05cm} \vert \hspace{0.05cm}\right )}.$$
- Die 2D–Wahrscheinlichkeitsdichtefunktion oder kurz $\rm 2D\hspace{-0.1cm}-\hspace{-0.1cm}WDF$ ist eine Erweiterung der eindimensionalen WDF.
- $X$ und $Y$ bezeichnen die beiden Zufallsgrößen, und $x \in X$ sowie $y \in Y$ geben Realisierungen hiervon an.
- Die für dieses Applet verwendete Nomenklatur unterscheidet sich also geringfügig gegenüber der Beschreibung im Theorieteil.
- Im hier betrachteten Fall „Statistische Unabhängigkeit” ist das Maximum der 2D–WDF wie folgt gegeben:
- $$f_{XY}(x, \ y)=\frac{\lambda_X \cdot \lambda_Y} {4}.$$
- Aus der Bedingungsgleichung $f_{XY}(x, y) = {\rm const.}$ können die Höhenlinien der WDF berechnet werden. Beschriftet man die Höhenlinien mit dem Verhältnis $V$ der entsprechenden $f_{XY}(x, y)$–Werte auf das Maximum, so erhält man als Gleichung für die Höhenlinien:
- $$\lambda_X \hspace{0.05cm} \cdot \hspace{0.05cm} \vert \hspace{0.05cm} x \hspace{0.05cm} \vert+ \lambda_Y \hspace{0.05cm} \cdot \hspace{0.05cm} \vert \hspace{0.05cm} y \hspace{0.05cm} \vert \hspace{0.05cm} =\ln \ (1/V) = K.$$
- Beispielsweise gilt für die $10\%$–Höhenlinie $K = \ln \ 10 \approx 2.3$ und für die $50\%$–Höhenlinie $K = \ln \ 2 \approx 0.693$.
- Die Höhenlinien beschreiben in jedem Quadranten Geradenstücke und ergeben insgesamt Vierecke mit den Eckpunkten auf der $x$– und $y$–Achse.
Zweidimensionale Verteilungsfunktion ⇒ 2D–VTF
Die 2D-Verteilungsfunktion ist ebenso wie die 2D-WDF lediglich eine sinnvolle Erweiterung der eindimensionalen Verteilungsfunktion (VTF):
- $$F_{XY}(x,y) = {\rm Pr}\big [(X \le x) \cap (Y \le y) \big ] .$$
Es ergeben sich folgende Gemeinsamkeiten und Unterschiede zwischen der „1D-VTF” und der„ 2D-VTF”:
- Der Funktionalzusammenhang zwischen „2D–WDF” und „2D–VTF” ist wie im eindimensionalen Fall durch die Integration gegeben, aber nun in zwei Dimensionen. Bei kontinuierlichen Zufallsgrößen gilt:
- $$F_{XY}(x,y)=\int_{-\infty}^{y} \int_{-\infty}^{x} f_{XY}(\xi,\eta) \,\,{\rm d}\xi \,\, {\rm d}\eta .$$
- Umgekehrt lässt sich die Wahrscheinlichkeitsdichtefunktion aus der Verteilungsfunktion durch partielle Differentiation nach $x$ und $y$ angeben:
- $$f_{XY}(x,y)=\frac{{\rm d}^{\rm 2} F_{XY}(\xi,\eta)}{{\rm d} \xi \,\, {\rm d} \eta}\Bigg|_{\left.{x=\xi \atop {y=\eta}}\right.}.$$
- Bezüglich der Verteilungsfunktion $F_{XY}(x, y)$ gelten folgende Grenzwerte:
- $$F_{XY}(-\infty,\ -\infty) = 0,\hspace{0.5cm}F_{XY}(x,\ +\infty)=F_{X}(x ),\hspace{0.5cm} F_{XY}(+\infty,\ y)=F_{Y}(y ) ,\hspace{0.5cm}F_{XY}(+\infty,\ +\infty) = 1.$$
- Im Grenzfall $($unendlich große $x$ und $y)$ ergibt sich demnach für die „2D-VTF” der Wert $1$. Daraus erhält man die Normierungsbedingung für die 2D-Wahrscheinlichkeitsdichtefunktion:
- $$\int_{-\infty}^{+\infty} \int_{-\infty}^{+\infty} f_{XY}(x,y) \,\,{\rm d}x \,\,{\rm d}y=1 . $$
$\text{Fazit:}$ Beachten Sie den signifikanten Unterschied zwischen eindimensionalen und zweidimensionalen Zufallsgrößen:
- Bei eindimensionalen Zufallsgrößen ergibt die Fläche unter der WDF stets den Wert $1$.
- Bei zweidimensionalen Zufallsgrößen ist das WDF-Volumen immer gleich $1$.
Versuchsdurchführung
- Wählen Sie zunächst die Nummer (1, ...) der zu bearbeitenden Aufgabe.
- Eine Aufgabenbeschreibung wird angezeigt. Die Parameterwerte sind angepasst.
- Lösung nach Drücken von „Musterlösung”.
Die Nummer 0 entspricht einem „Reset”:
- Gleiche Einstellung wie beim Programmstart.
- Ausgabe eines „Reset–Textes” mit weiteren Erläuterungen zum Applet.
(1) Welche 1D–WDF–Werte $f_X(x=1)$ bzw. $f_Y(y=1)$ ergeben sich für $\lambda_X=1$ und $\lambda_Y=2$ ? Wie lauten die WDF–Werte $f_X(x=-1)$ bzw. $f_Y(y=-1)$ ?
- Es gilt $f_{X}(x= 1)=0.5\cdot{\rm e}^ { - 1} = 0.1839$ und $f_{Y}(y= 1)=1\cdot{\rm e}^ { - 2} = 0.1353$.
- Aufgrund der Symmetrie gilt auch $f_{X}(x= -1)= 0.1839$ und $f_{Y}(y= -1)= 0.1353$.
(2) Welche 1D–VTF–Werte $F_X(x=1)$ bzw. $F_Y(y=1)$ ergeben sich für $\lambda_X=1$ und $\lambda_Y=2$ ? Wie lauten die VTF–Werte $F_X(x=-1)$ bzw. $F_Y(y=-1)$ ?
- Es gilt $F_{X}(x= 1)=0.5 + 0.5 \cdot\big [1-{\rm e}^ { - 1}\big] = 0.8161$ und $F_{Y}(y= 1)=0.5 + 0.5 \cdot\big [1-{\rm e}^ { - 2}\big] = 0.9323.$
- Wegen ${\rm sign}(-1) = -1$ erhält man $F_{X}(x= -1)=0.5 - 0.5 \cdot\big [1-{\rm e}^ { - 1}\big] = 0.1839$ und $F_{Y}(y=- 1)=0.5 - 0.5 \cdot\big [1-{\rm e}^ { - 2}\big] = 0.0677.$
(3) Es gelte $\lambda_X=1$ und $\lambda_Y=1$ . Wie groß sind die Wahrscheinlichkeiten ${\rm Pr}(X< 1)$, ${\rm Pr}(X\le 1)$, ${\rm Pr}(X\le -1)$ und ${\rm Pr}(-1\le X\le +1)$ ?
- Es gilt ${\rm Pr}(X< 1)=F_{X}(x= 1)=0.8161$. Bei einer wertdiskreten Zufallsgröße ist ${\rm Pr}(X\equiv 1)=0$ ⇒ ${\rm Pr}(X\le 1)={\rm Pr}(X< 1)=0.8161$.
- Weiter gilt ${\rm Pr}(X< -1)=F_{X}(x= -1)=0.1839$ sowie ${\rm Pr}(-1\le X\le +1)=F_{X}(x= +1) - F_{X}(x= -1)= 0.8161-0.1839 = 0.6322$.
(4) Betrachten Sie nun die 2D–WDF für $\lambda_X=1$ und $\lambda_Y=1$ ? Wie lauten die 2D–WDF–Werte $f_{XY}(0, \ 0)$ und $f_{XY}(2.3, \ 0)$ ?
- Mit diesen Parametern ist das Maximum $f_{XY}(0, \ 0)=0.25$ und der 2D–WDF–Wert $f_{XY}(2.3, \ 0)=0.025064 \approx f_{XY}(0, \ 0)/10$.
- Der Punkt $(2.3, \ 0)$ liegt somit (näherungsweise) auf der $10\%$–Höhenlinie, die hier ein um $45^\circ$ gedrehtes Quadrat ergibt.
(5) Wie lauten die 2D–WDF–Werte $f_{XY}(1.1, \ 1.2)$, $f_{XY}(-1.1, \ -1.2)$ und $f_{XY}(0.6, \ -1.7)$ ?
- Jeder Punkt $(x_0, \ y_0)$ liegt auf der $10\%$–Höhenlinie, wenn $\vert x_0 \vert + \vert y_0 \vert = \ln(10) \approx 2.3$ gilt.
- Die drei hier abgefragten Punkte erfüllen diese Bedingung mit hinreichender Genauigkeit.
(6) Nun gelte $\lambda_X=2$ und $\lambda_Y=1$ ? Wie lautet die Geichung der $10\%$–Höhenlinie im ersten Quadranten ? Kontrollieren Sie das Ergebnis.
- Für alle Höhenlinien muss im ersten Quadranten gelten: $\lambda_Y \cdot y_0 = K - \lambda_X \cdot x_0.$ Für die $10\%$–Höhenlinie ist wieder $K= \ln (1/0.01) = 2.3$ zu setzen.
- Daraus folgt: $y_0 = - \lambda_X/\lambda_Y \cdot x_0 + K/\lambda_Y = -2 \cdot x_0 + 2.3.$ Schnittpunkte mit den Achsen: $(1.15, \ 0)$ und $(0, \ 2.3)$.
- Das Programm bestätigt das Ergebnis: Maximum $f_{XY}(0, \ 0) = 0.5$. Bei den genannten Punkten gilt $f_{XY}(x_0, \ y_0) = 0.05013 \approx 10\%$.
(7) Betrachten Sie nun die 2D–VTF für $\lambda_X=1$ und $\lambda_Y=1$ ? Wie lauten die 2D–VTF–Werte $F_{XY}(0, 0)$, $F_{XY}(-3, \ -\hspace{-0.1cm}3)$ und $F_{XY}(+3, \ +\hspace{-0.1cm}3)$ ?
- Es gilt $F_{XY}(0, \ 0) = 0.25$. Dies entspricht der Wahrscheinlichkeit ${\rm Pr}\big [( X \le 0) \cap ( Y \le 0) \big ] = 0.5^2.$
- Es gilt $F_{XY}(-3, \ -\hspace{-0.1cm}3) \approx 0$ und $F_{XY}(+3, \ +\hspace{-0.1cm}3) \approx 0.9508$ ⇒ Im Gegensatz zur 1D–VTF gilt hier nicht: $F_{XY}(+3, \ +\hspace{-0.1cm}3) = 1 - F_{XY}(-3, \ -\hspace{-0.1cm}3)$.
(8) Die Einstellungen bleiben erhalten. Wie lauten die 2D–VTF–Werte $F_{XY}(+1, \ +\hspace{-0.1cm}1)$, $F_{XY}(+1, \ -\hspace{-0.1cm}1)$, $F_{XY}(-1, \ +\hspace{-0.1cm}1)$ und $F_{XY}(-1, \ -\hspace{-0.1cm}1)$ ?
Wie groß ist die Wahrscheinlichkeit ${\rm Pr}\big [(\vert X \vert \le 1) \cap (\vert Y \vert \le 1) \big ] .$
- Die gesuchten 2D–VTF–Werte sind $F_{XY}(+1, \ +\hspace{-0.1cm}1) = 0.6659$, $F_{XY}(+1, \ -\hspace{-0.1cm}1)= 0.1501$, $F_{XY}(-1, \ +\hspace{-0.1cm}1)= 0.1501$ und $F_{XY}(-1, \ -\hspace{-0.1cm}1)= 0.0338$.
- In der Teilaufgabe (3) wurde berechnet: ${\rm Pr}(-1\le X\le +1) = {\rm Pr}(\vert X \vert \le 1) = 0.6322$. Wegen $\lambda_X=\lambda_Y=1$ gilt auch ${\rm Pr}(\vert Y \vert \le 1) = 0.6322$.
- Aufgrund der statistischen Unabhängigkeit gilt dann für die Verbundwahrscheinlichkeit: ${\rm Pr}\big [(\vert X \vert \le 1) \cap (\vert Y \vert \le 1) \big ] = 0.6322^2= 0.3997.$
- Zum gleichen Ergebnis kommt man mit den 2D–VTF–Werten entsprechend der folgenden Gleichung:
$\hspace{2cm}{\rm Pr}\big [(\vert X \vert \le 1) \cap (\vert Y \vert \le 1) \big ] = F_{XY}(+1, \ +\hspace{-0.1cm}1) - F_{XY}(+1, \ -\hspace{-0.1cm}1) - F_{XY}(-1, \ +\hspace{-0.1cm}1) + F_{XY}(-1, \ -\hspace{-0.1cm}1)=0.6659 - 2 \cdot 0.1501 + 0.0338.$
Zur Handhabung des Applets
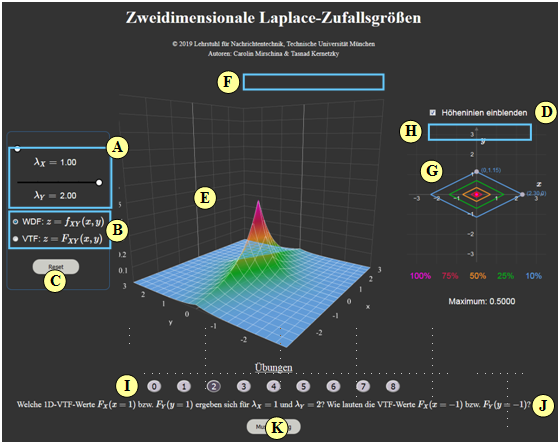
(A) Parametereingabe per Slider: $\lambda_X$ und $\lambda_Y$
(B) Auswahl: Darstellung von WDF oder VTF
(C) Reset: Einstellung wie beim Programmstart
(D) Höhenlinien darstellen oder „1D-WDF”
(E) Darstellungsbereich für „2D-WDF”
(F) Manipulation der 3D-Grafik (Zoom, Drehen, ...)
(G) Darstellungsbereich für „Höhenlinien” bzw. „1D-WDF”
(H) Manipulation der 2D-Grafik („1D-WDF”)
( I ) Bereich für die Versuchsdurchführung: Aufgabenauswahl
(J) Bereich für die Versuchsdurchführung: Aufgabenstellung
(K) Bereich für die Versuchsdurchführung: Musterlösung einblenden
Werte–Ausgabe über Maussteuerung (sowohl bei 2D als auch bei 3D)
Über die Autoren
Dieses interaktive Berechnungstool wurde am Lehrstuhl für Nachrichtentechnik der Technischen Universität München konzipiert und realisiert.
- Die erste Version wurde 2003 von Ji Li im Rahmen ihrer Diplomarbeit mit „FlashMX–Actionscript” erstellt (Betreuer: Günter Söder).
- 2019 wurde das Programm von Carolin Mirschina im Rahmen einer Werkstudententätigkeit auf „HTML5” umgesetzt und neu gestaltet (Betreuer: Tasnád Kernetzky).
Die Umsetzung dieses Applets auf HTML 5 wurde durch Studienzuschüsse der Fakultät EI der TU München finanziell unterstützt. Wir bedanken uns.