Difference between revisions of "Aufgaben:Exercise 1.2Z: Puls Code Modulation"
From LNTwww
m (Text replacement - "[[Signaldarstellung/" to "[[Signal_Representation/") |
|||
| Line 2: | Line 2: | ||
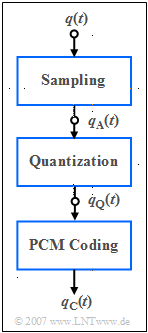
| − | [[File:EN_Sig_Z_1_2.png|right|frame| | + | [[File:EN_Sig_Z_1_2.png|right|frame|Components of pulse code modulation]] |
| − | + | All modern communication systems are digital. The principle of digital transmission of speech signals goes back to [https://de.wikipedia.org/wiki/Alec_Reeves Alec Reeves] , who invented the so-called ''Pulscodemodulation'' ('''PCM''') already at 1938. | |
| − | + | On the right you see the (simplified) block diagram of the PCM transmitter with three functional units: | |
| − | * | + | *The band-limited speech signal ${q(t)}$ is sampled, where the [[Signal_Representation/Zeitdiskrete_Signaldarstellung#Das_Abtasttheorem|Abtasttheorem]] is observed, and yields the sampled signal $q_{\rm A}(t)$. |
| − | * | + | * Each sample $q_{\rm A}(t)$ is mapped to one of $M = 2^N$ and results in the quantized signal $q_{\rm Q}(t)$. |
| − | * | + | * Each individual quantized value is represented by a code sequence of $N$ binary symbols and results in the coded signal $q_{\rm C}(t)$. |
| − | In | + | In this task only the different signals of the PCM transmitter are to be classified. Later tasks will deal with other properties of pulse code modulation. |
| Line 18: | Line 18: | ||
| − | '' | + | ''Notes:'' This task belongs to the chapter [[Signal_Representation/Klassifizierung_von_Signalen|Klassifizierung von Signalen]]. |
| − | === | + | ===Questions=== |
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Which of the statements are true for the source signal ${q(t)}$ ? |
|type="[]"} | |type="[]"} | ||
| − | + | + | + In normal operation ${q(t)}$ is a stochastic signal. |
| − | + | + | + A deterministic source signal is only useful in test operation or for theoretical investigations. |
| − | - ${q(t)}$ | + | - ${q(t)}$ is a time-discrete signal. |
| − | + ${q(t)}$ | + | + ${q(t)}$ is a continuous value signal. |
| − | { | + | {Which of the statements apply to the sampled signal $q_{\rm A}(t)$ ? |
|type="[]"} | |type="[]"} | ||
| − | - $q_{\rm A}(t)$ | + | - $q_{\rm A}(t)$ is a discrete-valued signal. |
| − | + $q_{\rm A}(t)$ | + | + $q_{\rm A}(t)$ is a time-discrete signal. |
| − | + | + | + The higher the maximum frequency of the message signal, the higher the sampling rate must be selected. |
| − | { | + | {Which statements are true for the quantized signal $q_{\rm Q}(t)$ if $N = 8$ is taken as a base? |
|type="[]"} | |type="[]"} | ||
| − | + $q_{\rm Q}(t)$ | + | + $q_{\rm Q}(t)$ is a time-discrete signal. |
| − | - $q_{\rm Q}(t)$ | + | - $q_{\rm Q}(t)$ is a discrete-valued with signal $M = 8$ possible values. |
| − | + $q_{\rm Q}(t)$ | + | + $q_{\rm Q}(t)$ is a discrete-valued with signal $M = 256$ possible values. |
| − | - $q_{\rm Q}(t)$ | + | - $q_{\rm Q}(t)$ is a binary signal. |
| − | { | + | {Which statements are true for the coded signal $q_{\rm C}(t)$ if $N = 8$ is taken as a basis? |
|type="[]"} | |type="[]"} | ||
| − | + $q_{\rm C}(t)$ | + | + $q_{\rm C}(t)$ is a time-discrete signal. |
| − | - $q_{\rm C}(t)$ | + | - $q_{\rm C}(t)$ is a discrete-valued signal with $M = 8$ possible values. |
| − | + $q_{\rm C}(t)$ | + | + $q_{\rm C}(t)$ is a binary signal. |
| − | - | + | - When sampling at distance $T_{\rm A}$ the bit duration is $T_{\rm B} = T_{\rm A}$. |
| − | + | + | + For sampling at distance $T_{\rm A}$ the bit duration is $T_{\rm B} = T_{\rm A}/8$. |
| Line 60: | Line 60: | ||
</quiz> | </quiz> | ||
| − | === | + | ===Solutions=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
'''(1)''' Richtig sind die <u>Lösungsvorschläge 1, 2 und 4</u>: | '''(1)''' Richtig sind die <u>Lösungsvorschläge 1, 2 und 4</u>: | ||
Revision as of 19:14, 13 August 2020
All modern communication systems are digital. The principle of digital transmission of speech signals goes back to Alec Reeves , who invented the so-called Pulscodemodulation (PCM) already at 1938.
On the right you see the (simplified) block diagram of the PCM transmitter with three functional units:
- The band-limited speech signal ${q(t)}$ is sampled, where the Abtasttheorem is observed, and yields the sampled signal $q_{\rm A}(t)$.
- Each sample $q_{\rm A}(t)$ is mapped to one of $M = 2^N$ and results in the quantized signal $q_{\rm Q}(t)$.
- Each individual quantized value is represented by a code sequence of $N$ binary symbols and results in the coded signal $q_{\rm C}(t)$.
In this task only the different signals of the PCM transmitter are to be classified. Later tasks will deal with other properties of pulse code modulation.
Notes: This task belongs to the chapter Klassifizierung von Signalen.
Questions
Solutions
(1) Richtig sind die Lösungsvorschläge 1, 2 und 4:
- Das Quellensignal ${q(t)}$ ist analog, also wert- und zeitkontinuierlich.
- Im Allgemeinen macht es keinen Sinn, ein deterministisches Signal zu übertragen.
- Für die mathematische Beschreibung eignet sich ein deterministisches Quellensignal – wie zum Beispiel ein periodisches Signal – besser als ein Zufallssignal.
- Deterministische Signale werden auch für den Testbetrieb herangezogen, um erkannte Fehlfunktionen rekonstruieren zu können.
(2) Richtig sind die Lösungsvorschläge 2 und 3:
- Das Signal $q_{\rm A}(t)$ nach der Abtastung ist weiterhin wertkontinuierlich, aber nun zeitdiskret.
- Die Abtastfrequenz $f_{\rm A}$ ist dabei durch das so genannte Abtasttheorem vorgegeben.
- Je größer die maximale Frequenz $f_{\rm N,\,max}$ des Nachrichtensignals ist, desto größer muss $f_{\rm A} ≥ 2 \cdot f_{\rm N,\,max}$ gewählt werden.
(3) Richtig sind die Lösungsvorschläge 1 und 3:
- Das quantisierte Signal $q_{\rm Q}(t)$ ist zeit- und wertdiskret, wobei die Stufenzahl $M = 2^8 = 256$ beträgt.
- Ein Binärsignal ist dagegen ein wertdiskretes Signal mit der Stufenzahl $M = 2$.
(4) Richtig sind hier die Lösungsvorschläge 1, 3 und 5:
- Das codierte Signal $q_{\rm C}(t)$ ist binär $($Stufenzahl $M = 2)$ mit Bitdauer $T_{\rm B} = T_{\rm A}/8$.