Difference between revisions of "Signal Representation/Discrete Fourier Transform (DFT)"
m (Text replacement - "Signal_Representation/Fouriertransformation_und_-rücktransformation" to "Signal_Representation/Fourier_Transform_and_Its_Inverse") |
m (Text replacement - "Signal_Representation/Zeitdiskrete_Signaldarstellung" to "Signal_Representation/Time_Discrete_Signal_Representation") |
||
| Line 42: | Line 42: | ||
[[File:P_ID1132__Sig_T_5_1_S2_neu.png|center|frame|Diskretisierung im Zeitbereich – Periodifizierung im Frequenzbereich]] | [[File:P_ID1132__Sig_T_5_1_S2_neu.png|center|frame|Diskretisierung im Zeitbereich – Periodifizierung im Frequenzbereich]] | ||
| − | Entsprechend dem Kapitel [[Signal_Representation/ | + | Entsprechend dem Kapitel [[Signal_Representation/Time_Discrete_Signal_Representation|Zeitdiskrete Signaldarstellung]] kann man die Abtastung des Zeitsignals $x(t)$ durch die Multiplikation mit einem Diracpuls $p_{\delta}(t)$ beschreiben. Es ergibt sich das im Abstand $T_{\rm A}$ abgetastete Zeitsignal |
:$${\rm A}\{x(t)\} = \sum_{\nu = - \infty }^{+\infty} T_{\rm A} \cdot x(\nu \cdot T_{\rm A})\cdot | :$${\rm A}\{x(t)\} = \sum_{\nu = - \infty }^{+\infty} T_{\rm A} \cdot x(\nu \cdot T_{\rm A})\cdot | ||
| Line 54: | Line 54: | ||
P}= {1}/{T_{\rm A}}\hspace{0.05cm}.$$ | P}= {1}/{T_{\rm A}}\hspace{0.05cm}.$$ | ||
| − | Dieser Zusammenhang wurde ebenfalls bereits im Kapitel [[Signal_Representation/ | + | Dieser Zusammenhang wurde ebenfalls bereits im Kapitel [[Signal_Representation/Time_Discrete_Signal_Representation|Zeitdiskrete Signaldarstellung]] hergeleitet, jedoch mit etwas anderer Nomenklatur: |
*Das abgetastete Signal bezeichnen wir nun mit $\text{A}\{ x(t)\}$ anstelle von $x_{\rm A}(t)$. | *Das abgetastete Signal bezeichnen wir nun mit $\text{A}\{ x(t)\}$ anstelle von $x_{\rm A}(t)$. | ||
* Die '''Frequenzperiode''' wird nun mit $f_{\rm P} = 1/T_{\rm A}$ anstelle von $f_{\rm A} = 1/T_{\rm A}$ bezeichnet. | * Die '''Frequenzperiode''' wird nun mit $f_{\rm P} = 1/T_{\rm A}$ anstelle von $f_{\rm A} = 1/T_{\rm A}$ bezeichnet. | ||
Revision as of 14:26, 1 September 2020
Contents
- 1 Argumente für die diskrete Realisierung der Fouriertransformation
- 2 Zeitdiskretisierung – Periodifizierung im Frequenzbereich
- 3 Frequenzdiskretisierung – Periodifizierung im Zeitbereich
- 4 Finite Signaldarstellung
- 5 Von der kontinuierlichen zur diskreten Fouriertransformation
- 6 Inverse Diskrete Fouriertransformation
- 7 Interpretation von DFT und IDFT
- 8 Aufgaben zum Kapitel
Argumente für die diskrete Realisierung der Fouriertransformation
Die Fouriertransformation gemäß der bisherigen Beschreibung im Kapitel Aperiodische Signale – Impulse weist aufgrund der unbegrenzten Ausdehnung des Integrationsintervalls eine unendlich hohe Selektivität auf und ist deshalb ein ideales theoretisches Hilfsmittel der Spektralanalyse.
Sollen die Spektralanteile $X(f)$ einer Zeitfunktion $x(t)$ numerisch ermittelt werden, so sind die allgemeinen Transformationsgleichungen
- $$\begin{align*}X(f) & = \int_{-\infty }^{+\infty}x(t) \cdot {\rm e}^{-{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2 \pi f t}\hspace{0.1cm} {\rm d}t\hspace{0.5cm} \Rightarrow\hspace{0.5cm} \text{Hintransformation}\hspace{0.7cm} \Rightarrow\hspace{0.5cm} \text{Erstes Fourierintegral} \hspace{0.05cm},\\ x(t) & = \int_{-\infty }^{+\infty}\hspace{-0.15cm}X(f) \cdot {\rm e}^{\hspace{0.05cm}+{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2 \pi f t}\hspace{0.1cm} {\rm d}f\hspace{0.35cm} \Rightarrow\hspace{0.5cm} \text{Rücktransformation}\hspace{0.4cm} \Rightarrow\hspace{0.5cm} \text{Zweites Fourierintegral} \hspace{0.05cm}\end{align*}$$
aus zwei Gründen ungeeignet:
- Die Gleichungen gelten ausschließlich für zeitkontinuierliche Signale. Mit Digitalrechnern oder Signalprozessoren kann man jedoch nur zeitdiskrete Signale verarbeiten.
- Für eine numerische Auswertung der beiden Fourierintegrale ist es erforderlich, das jeweilige Integrationsintervall auf einen endlichen Wert zu begrenzen.
$\text{Daraus ergibt sich folgende Konsequenz:}$
Ein kontinuierliches Signal muss vor der numerischen Bestimmung seiner Spektraleigenschaften zwei Prozesse durchlaufen, nämlich
- den der Abtastung zur Diskretisierung, und
- den der Fensterung zur Begrenzung des Integrationsintervalls.
Im Folgenden wird ausgehend von einer aperiodischen Zeitfunktion $x(t)$ und dem dazugehörigen Fourierspektrum $X(f)$ eine für die Rechnerverarbeitung geeignete zeit– und frequenzdiskrete Beschreibung schrittweise entwickelt.
Zeitdiskretisierung – Periodifizierung im Frequenzbereich
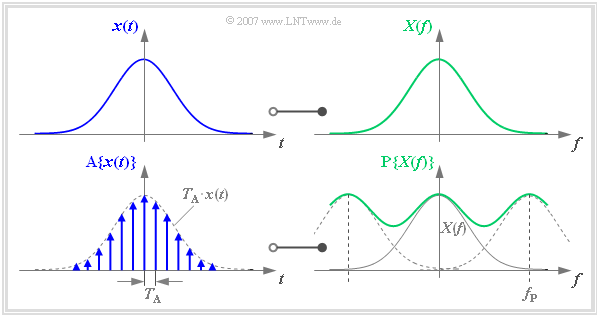
Die folgenden Grafiken zeigen einheitlich links den Zeitbereich und rechts den Frequenzbereich. Ohne Einschränkung der Allgemeingültigkeit sind $x(t)$ und $X(f)$ jeweils reell und gaußförmig.
Entsprechend dem Kapitel Zeitdiskrete Signaldarstellung kann man die Abtastung des Zeitsignals $x(t)$ durch die Multiplikation mit einem Diracpuls $p_{\delta}(t)$ beschreiben. Es ergibt sich das im Abstand $T_{\rm A}$ abgetastete Zeitsignal
- $${\rm A}\{x(t)\} = \sum_{\nu = - \infty }^{+\infty} T_{\rm A} \cdot x(\nu \cdot T_{\rm A})\cdot \delta (t- \nu \cdot T_{\rm A} )\hspace{0.05cm}.$$
Dieses abgetastete Signal $\text{A}\{ x(t)\}$ transformieren wir nun in den Frequenzbereich. Der Multiplikation des Diracpulses $p_{\delta}(t)$ mit $x(t)$ entspricht im Frequenzbereich die Faltung von $P_{\delta}(f)$ mit $X(f)$. Es ergibt sich das periodifizierte Spektrum $\text{P}\{ X(f)\}$, wobei $f_{\rm P}$ die Frequenzperiode der Funktion $\text{P}\{ X(f)\}$ angibt:
- $${\rm A}\{x(t)\} \hspace{0.2cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, \hspace{0.2cm} {\rm P}\{X(f)\} = \sum_{\mu = - \infty }^{+\infty} X (f- \mu \cdot f_{\rm P} )\hspace{0.5cm} {\rm mit }\hspace{0.5cm}f_{\rm P}= {1}/{T_{\rm A}}\hspace{0.05cm}.$$
Dieser Zusammenhang wurde ebenfalls bereits im Kapitel Zeitdiskrete Signaldarstellung hergeleitet, jedoch mit etwas anderer Nomenklatur:
- Das abgetastete Signal bezeichnen wir nun mit $\text{A}\{ x(t)\}$ anstelle von $x_{\rm A}(t)$.
- Die Frequenzperiode wird nun mit $f_{\rm P} = 1/T_{\rm A}$ anstelle von $f_{\rm A} = 1/T_{\rm A}$ bezeichnet.
Diese Nomenklaturänderungen werden auf den folgenden Seiten begründet.
Die obige Grafik zeigt den hier beschriebenen Funktionalzusammenhang. Es ist anzumerken:
- Die Frequenzperiode $f_{\rm P}$ wurde hier bewusst klein gewählt, so dass die Überlappung der zu summierenden Spektren deutlich zu erkennen ist.
- In der Praxis sollte $f_{\rm P}$ aufgrund des Abtasttheorems mindestens doppelt so groß sein wie die größte im Signal $x(t)$ enthaltene Frequenz.
- Ist dies nicht erfüllt, so muss mit Aliasing gerechnet werden – siehe Kapitel Fehlermöglichkeiten bei Anwendung der DFT.
Frequenzdiskretisierung – Periodifizierung im Zeitbereich
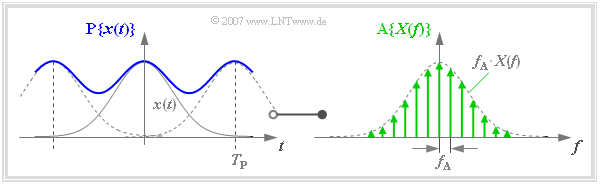
Die Diskretisierung von $X(f)$ lässt sich ebenfalls durch eine Multiplikation mit einem Diracpuls beschreiben. Es ergibt sich das im Abstand $f_{\rm A}$ abgetastete Spektrum:
- $${\rm A}\{X(f)\} = X(f) \cdot \sum_{\mu = - \infty }^{+\infty} f_{\rm A} \cdot \delta (f- \mu \cdot f_{\rm A } ) = \sum_{\mu = - \infty }^{+\infty} f_{\rm A} \cdot X(\mu \cdot f_{\rm A } ) \cdot\delta (f- \mu \cdot f_{\rm A } )\hspace{0.05cm}.$$
Transformiert man den hier verwendeten Frequenz–Diracpuls $($mit Impulsgewichten $f_{\rm A})$ in den Zeitbereich, so erhält man mit $T_{\rm P} = 1/f_{\rm A}$:
- $$\sum_{\mu = - \infty }^{+\infty} f_{\rm A} \cdot \delta (f- \mu \cdot f_{\rm A } ) \hspace{0.2cm}\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ\, \hspace{0.2cm} \sum_{\nu = - \infty }^{+\infty} \delta (t- \nu \cdot T_{\rm P } ) \hspace{0.05cm}.$$
Die Multiplikation mit $X(f)$ entspricht im Zeitbereich der Faltung mit $x(t)$. Man erhält das im Abstand $T_{\rm P}$ periodifizierte Signal $\text{P}\{ x(t)\}$:
- $${\rm A}\{X(f)\} \hspace{0.2cm}\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ\, \hspace{0.2cm} {\rm P}\{x(t)\} = x(t) \star \sum_{\nu = - \infty }^{+\infty} \delta (t- \nu \cdot T_{\rm P } )= \sum_{\nu = - \infty }^{+\infty} x (t- \nu \cdot T_{\rm P } ) \hspace{0.05cm}.$$
$\text{Beispiel 1:}$ Dieser Zusammenhang ist in der Grafik veranschaulicht:
- Aufgrund der groben Frequenzrasterung ergibt sich in diesem Beispiel für die Zeitperiode $T_{\rm P}$ ein relativ kleiner Wert.
- Deshalb unterscheidet sich das (blaue) periodifizierte Zeitsignal $\text{P}\{ x(t)\}$ aufgrund von Überlappungen deutlich von $x(t)$.
Finite Signaldarstellung
Zur so genannten finiten Signaldarstellung kommt man,
- wenn sowohl die Zeitfunktion $x(t)$
- als auch die Spektralfunktion $X(f)$
ausschließlich durch ihre Abtastwerte angegeben werden.
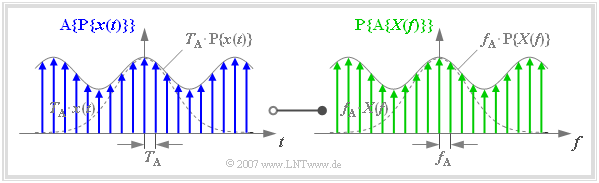
Die Grafik ist wie folgt zu interpretieren:
- Im linken Bild blau eingezeichnet ist die Funktion $\text{A}\{ \text{P}\{ x(t)\}\}$. Diese ergibt sich durch Abtastung der periodifizierten Zeitfunktion $\text{P}\{ x(t)\}$ mit äquidistanten Diracimpulsen im Abstand $T_{\rm A} = 1/f_{\rm P}$.
- Im rechten Bild grün eingezeichnet ist die Funktion $\text{P}\{ \text{A}\{ X(f)\}\}$. Diese ergibt sich durch Periodifizierung $($mit $f_{\rm P})$ der abgetasteten Spektralfunktion $\{ \text{A}\{ X(f)\}\}$.
- Zwischen dem blauen finiten Signal (linke Skizze) und dem grünen finiten Signal (rechte Skizze) besteht eine Fourierkorrespondenz, und zwar folgende:
- $${\rm A}\{{\rm P}\{x(t)\}\} \hspace{0.2cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, \hspace{0.2cm} {\rm P}\{{\rm A}\{X(f)\}\} \hspace{0.05cm}.$$
- Die Diraclinien der periodischen Fortsetzung $\text{P}\{ \text{A}\{ X(f)\}\}$ der abgetasteten Spektralfunktion fallen allerdings nur dann in das gleiche Frequenzraster wie diejenigen von $\text{A}\{ X(f)\}$, wenn die Frequenzperiode $f_{\rm P}$ ein ganzzahliges Vielfaches $(N)$ des Frequenzabtastabstandes $f_{\rm A}$ ist.
- Deshalb muss bei Anwendung der finiten Signaldarstellung stets die folgende Bedingung erfüllt sein, wobei die natürliche Zahl $N$ in der Praxis meist eine Zweierpotenz ist (obiger Grafik liegt der Wert $N = 8$ zugrunde):
- $$f_{\rm P} = N \cdot f_{\rm A} \hspace{0.5cm} \Rightarrow\hspace{0.5cm} {1}/{T_{\rm A}}= N \cdot f_{\rm A} \hspace{0.5cm} \Rightarrow\hspace{0.5cm} N \cdot f_{\rm A}\cdot T_{\rm A} = 1\hspace{0.05cm}.$$
- Bei Einhaltung der Bedingung $N \cdot f_{\rm A} \cdot T_{\rm A} = 1$ ist die Reihenfolge von Periodifizierung und Abtastung vertauschbar. Somit gilt:
- $${\rm A}\{{\rm P}\{x(t)\}\} = {\rm P}\{{\rm A}\{x(t)\}\}\hspace{0.2cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, \hspace{0.2cm} {\rm P}\{{\rm A}\{X(f)\}\} = {\rm A}\{{\rm P}\{X(f)\}\}\hspace{0.05cm}.$$
$\text{Fazit:}$
- Die Zeitfunktion $\text{P}\{ \text{A}\{ x(t)\}\}$ besitzt die Periode $T_{\rm P} = N \cdot T_{\rm A}$.
- Die Periode im Frequenzbereich ist $f_{\rm P} = N \cdot f_{\rm A}$.
- Zur Beschreibung des diskretisierten Zeit– und Frequenzverlaufs reichen somit jeweils $N$ komplexe Zahlenwerte in Form von Impulsgewichten aus.
$\text{Beispiel 2:}$ Es liegt ein zeitbegrenztes (impulsartiges) Signal $x(t)$ in abgetasteter Form vor, wobei der Abstand zweier Abtastwerte $T_{\rm A} = 1\, {\rm µ s}$ beträgt:
- Nach einer diskreten Fouriertransformation mit $N = 512$ liegt das Spektrum $X(f)$ in Form von Abtastwerten im Abstand $f_{\rm A} = (N \cdot T_{\rm A})^{–1} \approx 1.953\,\text{kHz} $ vor.
- Vergrößert man den DFT–Parameter auf $N= 2048$, so ergibt sich ein (vierfach) feineres Frequenzraster mit $f_{\rm A} \approx 488\,\text{Hz}$.
Von der kontinuierlichen zur diskreten Fouriertransformation
Aus dem herkömmlichen ersten Fourierintegral
- $$X(f) =\int_{-\infty }^{+\infty}x(t) \cdot {\rm e}^{-{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2 \pi \hspace{0.05cm}\cdot \hspace{0.05cm} f \hspace{0.05cm}\cdot \hspace{0.05cm}t}\hspace{0.1cm} {\rm d}t$$
entsteht durch Diskretisierung $(\text{d}t \to T_{\rm A}$, $t \to \nu \cdot T_{\rm A}$, $f \to \mu \cdot f_{\rm A}$, $T_{\rm A} \cdot f_{\rm A} = 1/N)$ die abgetastete und periodifizierte Spektralfunktion
- $${\rm P}\{X(\mu \cdot f_{\rm A})\} = T_{\rm A} \cdot \sum_{\nu = 0 }^{N-1} {\rm P}\{x(\nu \cdot T_{\rm A})\}\cdot {\rm e}^{-{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2 \pi \hspace{0.05cm} \cdot \hspace{0.05cm}\nu \hspace{0.05cm} \cdot \hspace{0.05cm}\mu /N} \hspace{0.05cm}.$$
Es ist berücksichtigt, dass aufgrund der Diskretisierung jeweils die periodifizierten Funktionen einzusetzen sind.
Aus Gründen einer vereinfachten Schreibweise nehmen wir nun die folgenden Substitutionen vor:
- Die $N$ Zeitbereichskoeffizienten seien mit der Laufvariablen $\nu = 0$, ... , $N - 1$:
- $$d(\nu) = {\rm P}\left\{x(t)\right\}{\big|}_{t \hspace{0.05cm}= \hspace{0.05cm}\nu \hspace{0.05cm}\cdot \hspace{0.05cm}T_{\rm A}}\hspace{0.05cm}.$$
- Die $N$ Frequenzbereichskoeffizienten seien mit der Laufvariablen $\mu = 0,$ ... , $N$ – 1:
- $$D(\mu) = f_{\rm A} \cdot {\rm P}\left\{X(f)\right\}{\big|}_{f \hspace{0.05cm}= \hspace{0.05cm}\mu \hspace{0.05cm}\cdot \hspace{0.05cm}f_{\rm A}}\hspace{0.05cm}.$$
- Abkürzend wird für den von $N$ abhängigen komplexen Drehfaktor geschrieben:
- $$w = {\rm e}^{-{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2 \pi /N} = \cos \left( {2 \pi}/{N}\right)-{\rm j} \cdot \sin \left( {2 \pi}/{N}\right) \hspace{0.05cm}.$$
$\text{Definition:}$
Unter dem Begriff Diskrete Fouriertransformation (kurz DFT) versteht man die Berechnung der $N$ Spektralkoeffizienten $D(\mu)$ aus den $N$ Signalkoeffizienten $d(\nu)$:
- $$D(\mu) = \frac{1}{N} \cdot \sum_{\nu = 0 }^{N-1} d(\nu)\cdot {w}^{\hspace{0.05cm}\nu \hspace{0.07cm} \cdot \hspace{0.05cm}\mu} \hspace{0.05cm}. $$
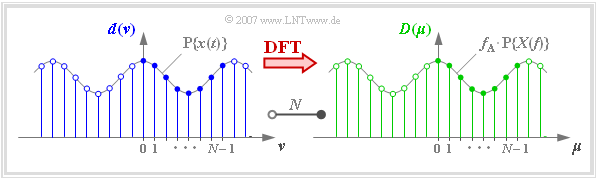
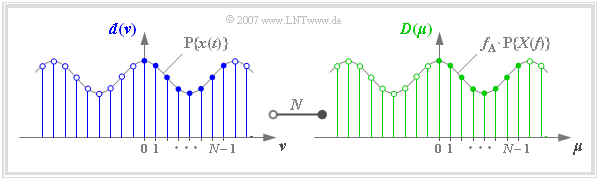
In der Grafik erkennt man an einem Beispiel
- die $N = 8$ Signalkoeffizienten $d(\nu)$ an der blauen Füllung,
- die $N = 8$ Spektralkoeffizienten $D(\mu)$ an der grünen Füllung.
Inverse Diskrete Fouriertransformation
Die Inverse Diskrete Fouriertransformation (IDFT) beschreibt das zweite Fourierintegral
- $$\begin{align*}x(t) & = \int_{-\infty }^{+\infty}X(f) \cdot {\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2 \pi \hspace{0.05cm}\cdot \hspace{0.05cm} f \hspace{0.05cm}\cdot \hspace{0.05cm} t}\hspace{0.1cm} {\rm d}f\end{align*}$$
in diskretisierter Form:
- $$d(\nu) = {\rm P}\left\{x(t)\right\}{\big|}_{t \hspace{0.05cm}= \hspace{0.05cm}\nu \hspace{0.05cm}\cdot \hspace{0.05cm}T_{\rm A}}\hspace{0.01cm}.$$
$\text{Definition:}$
Unter dem Begriff Inverse Diskreten Fouriertransformation (kurz IDFT) versteht man die Berechnung der Signalkoeffizienten $d(\nu)$ aus den Spektralkoeffizienten $D(\mu)$:
- $$d(\nu) = \sum_{\mu = 0 }^{N-1} D(\mu) \cdot {w}^{-\nu \hspace{0.07cm} \cdot \hspace{0.05cm}\mu} \hspace{0.05cm}.$$
Mit den Laufvariablen $\nu = 0, \hspace{0.05cm}\text{...} \hspace{0.05cm}, N-1$ und $\mu = 0, \hspace{0.05cm}\text{...} \hspace{0.05cm}, N-1$ gilt auch hier:
- $$d(\nu) = {\rm P}\left\{x(t)\right\}{\big \vert}_{t \hspace{0.05cm}= \hspace{0.05cm}\nu \hspace{0.05cm}\cdot \hspace{0.05cm}T_{\rm A} }\hspace{0.01cm},$$
- $$D(\mu) = f_{\rm A} \cdot {\rm P}\left\{X(f)\right\}{\big \vert}_{f \hspace{0.05cm}= \hspace{0.05cm}\mu \hspace{0.05cm}\cdot \hspace{0.05cm}f_{\rm A} } \hspace{0.01cm},$$
- $$w = {\rm e}^{- {\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2 \pi /N} \hspace{0.01cm}.$$
Ein Vergleich zwischen der DFT und IDFT zeigt, dass genau der gleiche Algorithmus verwendet werden kann. Die einzigen Unterschiede der IDFT gegenüber der DFT sind:
- Der Exponent des Drehfaktors ist mit unterschiedlichem Vorzeichen anzusetzen.
- Bei der IDFT entfällt die Division durch $N$.
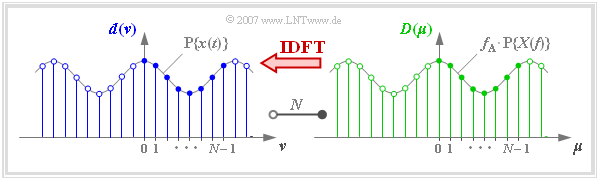
Interpretation von DFT und IDFT
Die Grafik zeigt die diskreten Koeffizienten im Zeit– und Frequenzbereich zusammen mit den periodifizierten zeitkontinuierlichen Funktionen.
Bei Anwendung von DFT bzw. IDFT ist zu beachten:
- Nach obigen Definitionen besitzen die DFT–Koeffizienten $d(ν)$ und $D(\mu)$ stets die Einheit der Zeitfunktion.
- Dividiert man $D(\mu)$ durch $f_{\rm A}$, so erhält man den Spektralwert $X(\mu \cdot f_{\rm A})$.
- Die Spektralkoeffizienten $D(\mu)$ müssen stets komplex angesetzt werden, um auch ungerade Zeitfunktionen berücksichtigen zu können.
- Um auch Bandpass–Signale im äquivalenten Tiefpass–Bereich transformieren zu können, verwendet man meist auch komplexe Zeitkoeffizienten $d(\nu)$.
- Als Grundintervall für $\nu$ und $\mu$ definiert man meist – wie in obiger Grafik – den Bereich von $0$ bis $N - 1$ (gefüllte Kreise in der Grafik).
- Mit den komplexwertigen Zahlenfolgen $\langle \hspace{0.1cm}d(\nu)\hspace{0.1cm}\rangle = \langle \hspace{0.1cm}d(0), \hspace{0.05cm}\text{...} \hspace{0.05cm} , d(N-1) \hspace{0.1cm}\rangle$ sowie $\langle \hspace{0.1cm}D(\mu)\hspace{0.1cm}\rangle = \langle \hspace{0.1cm}D(0), \hspace{0.05cm}\text{...} \hspace{0.05cm} , D(N-1) \hspace{0.1cm}\rangle$ werden DFT und IDFT ähnlich wie die herkömmliche Fouriertransformation symbolisiert:
- $$\langle \hspace{0.1cm} D(\mu)\hspace{0.1cm}\rangle \hspace{0.2cm}\bullet\!\!-\!\!\!-(N)\!-\!\!\!-\!\!\hspace{0.05cm}\circ\, \hspace{0.2cm} \langle \hspace{0.1cm} d(\nu) \hspace{0.1cm}\rangle \hspace{0.05cm}.$$
- Ist die Zeitfunktion $x(t)$ bereits auf den Bereich $0 \le t \lt N \cdot T_{\rm A}$ begrenzt, dann geben die von der IDFT ausgegebenen Zeitkoeffizienten direkt die Abtastwerte der Zeitfunktion an: $d(\nu) = x(\nu \cdot T_{\rm A}).$
- Ist $x(t)$ gegenüber dem Grundintervall verschoben, so muss man die im $\text{Beispiel 3}$ gezeigte Zuordnung zwischen $x(t)$ und den Koeffizienten $d(\nu)$ wählen.
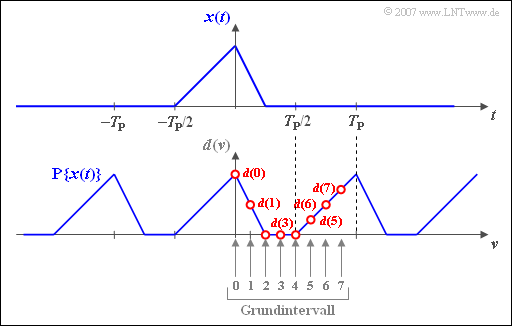
$\text{Beispiel 3:}$ Die obere Grafik zeigt den unsymmetrischen Dreieckimpuls $x(t)$, dessen absolute Breite kleiner ist als $T_{\rm P} = N \cdot T_{\rm A}$.
Die untere Skizze zeigt die zugeordneten DFT–Koeffizienten $($gültig für $N = 8)$.
- Für $\nu = 0,\hspace{0.05cm}\text{...} \hspace{0.05cm} , N/2 = 4$ gilt $d(\nu) = x(\nu \cdot T_{\rm A})$:
- $$d(0) = x (0)\hspace{0.05cm}, \hspace{0.15cm} d(1) = x (T_{\rm A})\hspace{0.05cm}, \hspace{0.15cm} d(2) = x (2T_{\rm A})\hspace{0.05cm}, $$
- $$d(3) = x (3T_{\rm A})\hspace{0.05cm}, \hspace{0.15cm} d(4) = x (4T_{\rm A})\hspace{0.05cm}.$$
- Dagegen sind die Koeffizienten $d(5)$, $d(6)$ und d$(7)$ wie folgt zu setzen:
- $$d(\nu) = x \big ((\nu\hspace{-0.05cm} - \hspace{-0.05cm} N ) \cdot T_{\rm A}\big ) $$
- $$ \Rightarrow \hspace{0.2cm}d(5) = x (-3T_{\rm A})\hspace{0.05cm}, \hspace{0.35cm} d(6) = x (-2T_{\rm A})\hspace{0.05cm}, \hspace{0.35cm} d(7) = x (-T_{\rm A})\hspace{0.05cm}.$$
Aufgaben zum Kapitel
Aufgabe 5.2: Inverse Diskrete Fouriertransformation
Aufgabe 5.2Z: DFT eines Dreieckimpulses