Difference between revisions of "Signal Representation/General Description"
m (Text replacement - "Zum Rechnen mit komplexen Zahlen" to "Calculating With Complex Numbers") |
|||
| Line 1: | Line 1: | ||
{{Header | {{Header | ||
| − | |Untermenü= | + | |Untermenü=Periodic Signals |
|Vorherige Seite=Calculating With Complex Numbers | |Vorherige Seite=Calculating With Complex Numbers | ||
| − | |Nächste Seite= | + | |Nächste Seite=Direct Current Signal - Limit Case of a Periodic Signal |
}} | }} | ||
| − | == # | + | == # OVERVIEW OF THE SECOND MAIN CHAPTER # == |
<br> | <br> | ||
| − | In | + | In this chapter ''periodic signals'' are considered and described mathematically in the time and frequency domain. |
| − | + | This chapter contains in detail: | |
| − | * | + | * Some basic terms like <i>period duration, fundamental frequency</i> and <i>circular frequency</i>, |
| − | * | + | * the properties of a <i>equal signal</i> as a boundary case of a periodic signal, |
| − | * | + | * the definition and interpretation of the <i>Dirac function</i>, |
| − | * | + | * the spectral representation of a <i>equal signal</i> or a <i>equal signal component</i>, |
| − | * | + | * the time– and frequency representation of <i>harmonic oscillations</i>, and finally |
| − | * | + | * the application of <i>Fourier series</i> for spectral analysis of periodic signals. |
| − | + | Further information on the topic as well as tasks, simulations and programming exercises can be found in | |
| − | * | + | *Chapter 6: ''Linear and Time Invariant Systems'' (Program lzi) |
| − | + | of the lab „Simulation Methods in Communication Engineering”. This former LNT course at the TU Munich is based on | |
| − | * | + | *the educational software package [http://en.lntwww.de/downloads/Sonstiges/Programme/LNTsim.zip LNTsim] ⇒ Link points to the ZIP version of the program, and |
| − | * | + | *this [http://en.lntwww.de/downloads/Sonstiges/Texte/Praktikum_LNTsim_Teil_A.pdf lab instruction] ⇒ Link refers to the PDF version of ; chapter 6: page 99-118. |
| − | == | + | ==Features and Applications== |
<br> | <br> | ||
| − | + | Periodic signals are of great importance for communications engineering: | |
| − | * | + | *They belong to the class of [[Signal_Representation/Signal_classification#Deterministische_und_stochastische_Signale|deterministic signals]], whose time function can be specified in analytical form. |
*Ihr Signalverlauf ist damit für alle Zeiten $t$ bekannt und für die Zukunft eindeutig vorhersagbar. | *Ihr Signalverlauf ist damit für alle Zeiten $t$ bekannt und für die Zukunft eindeutig vorhersagbar. | ||
*Sie sind daher niemals informationstragende Signale. | *Sie sind daher niemals informationstragende Signale. | ||
Revision as of 13:08, 26 September 2020
Contents
# OVERVIEW OF THE SECOND MAIN CHAPTER #
In this chapter periodic signals are considered and described mathematically in the time and frequency domain.
This chapter contains in detail:
- Some basic terms like period duration, fundamental frequency and circular frequency,
- the properties of a equal signal as a boundary case of a periodic signal,
- the definition and interpretation of the Dirac function,
- the spectral representation of a equal signal or a equal signal component,
- the time– and frequency representation of harmonic oscillations, and finally
- the application of Fourier series for spectral analysis of periodic signals.
Further information on the topic as well as tasks, simulations and programming exercises can be found in
- Chapter 6: Linear and Time Invariant Systems (Program lzi)
of the lab „Simulation Methods in Communication Engineering”. This former LNT course at the TU Munich is based on
- the educational software package LNTsim ⇒ Link points to the ZIP version of the program, and
- this lab instruction ⇒ Link refers to the PDF version of ; chapter 6: page 99-118.
Features and Applications
Periodic signals are of great importance for communications engineering:
- They belong to the class of deterministic signals, whose time function can be specified in analytical form.
- Ihr Signalverlauf ist damit für alle Zeiten $t$ bekannt und für die Zukunft eindeutig vorhersagbar.
- Sie sind daher niemals informationstragende Signale.
Trotzdem werden periodische Signale oft auch in der Nachrichtentechnik benötigt, zum Beispiel
- für die Modulation und Demodulation bei Trägerfrequenzsystemen,
- für die Synchronisation und Taktregenerierung bei Digitalsystemen,
- als Test– und Prüfsignale bei der Systemrealisierung.
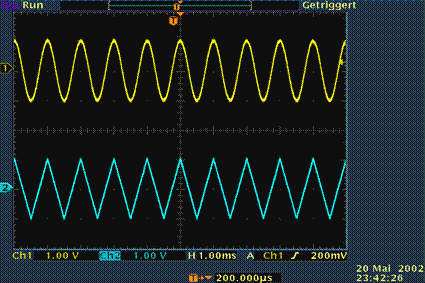
$\text{Beispiel 1:}$ Auf dem Oszilloskopbild sehen Sie zwei typische Vertreter periodischer Signale:
- oben ein Cosinussignal,
- unten ein Dreiecksignal.
Wie aus den eingeblendeten Einstellungen ersichtlich ist, beträgt bei beiden Signalen die Periodendauer eine Millisekunde und die Amplitude ein Volt.
Definition und Parameter
Bevor wir uns den Signalparametern eines periodischen Signals zuwenden, soll der Begriff „Periodizität” eindeutig definiert werden:
$\text{Definition:}$ Ein periodisches Signal $x(t)$ liegt dann vor, wenn für alle beliebigen Werte von $t$ und alle ganzzahligen Werte von $i$ mit einem geeigneten $T_{0}$ gilt:
- $$x(t+i\cdot T_{0}) = x(t).$$
Daraus ergeben sich die folgenden Kenngrößen:
- Die Periodendauer $T_{0}$ gibt den kleinstmöglichen Wert an, der obige Gleichung erfüllt.
- Die Grundfrequenz $f_{0} = 1/T_{0}$ beschreibt die Anzahl der Perioden pro Zeiteinheit (meist je Sekunde).
- Die Einheit „1/s” wird auch mit „Hz” bezeichnet, benannt nach dem deutschen Physiker Heinrich Hertz.
- Die Grundkreisfrequenz $\omega_{0}$ stellt die Winkeldrehung pro Sekunde dar, die meistens im Bogenmaß angegeben wird.
- Im Gegensatz zur Grundfrequenz ist hier nicht die Einheit „Hz”, sondern „1/s” üblich. Es gilt folgende Gleichung:
- $$\omega_{0}=2\pi f_{0} = {2\pi}/{T_{0}}.$$
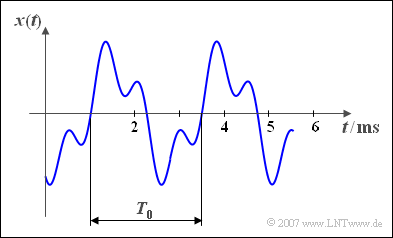
$\text{Beispiel 2:}$ Dargestellt ist hier ein periodisches Zeitsignal:
- Die Periodendauer beträgt $T_{0} = 2.5 \ \rm ms$.
- Daraus berechnet sich die Grundfrequenz $f_0 = 400 \ \rm Hz$.
- Die Grundkreisfrequenz ergibt sich zu $\omega_{0}=2513 \ \rm 1/s.$
Resultierende Periodendauer
Besteht ein Signal $x(t)$ aus der Summe zweier periodischer Signale $x_{1}(t)$ und $x_{2}(t)$ mit den Periodendauern $T_{1}$ bzw. $T_{2}$, so ist die resultierende Periodendauer des Summensignals das kleinste gemeinsame Vielfache von $T_{1}$ und $T_{2}$.
- Diese Aussage gilt unabhängig von den Amplituden– und Phasenverhältnissen.
- Besitzen $T_{1}$ und $T_{2}$ dagegen kein rationales gemeinsames Vielfaches $($Beispiel: $T_{2} = \pi \cdot T_{1})$, so ist das Summensignal $x(t)$ im Gegensatz zu seinen beiden Komponenten $x_{1}(t)$ und $x_{2}(t)$ nicht periodisch.
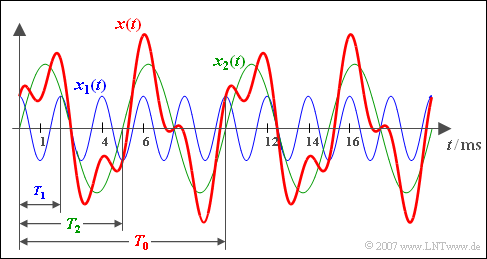
$\text{Beispiel 3:}$ Addiert werden ein cosinusförmiges Signal $x_{1}(t)$ mit der Periodendauer $T_{1} = 2\; {\rm ms}$ (blauer Signalverlauf) und ein Sinussignal $x_{2}(t)$ mit der Periodendauer $T_{2} = 5\; {\rm ms}$ und doppelt so großer Amplitude (grüner Verlauf).
- Das (rote) Summensignal $x(t) = x_{1}(t) + x_{2}(t)$ weist dann die resultierende Periodendauer $T_{0} = 10\; {\rm ms}$ auf ⇒ Grundfrequenz $f_{0} = 100\; {\rm Hz}$.
- Die Frequenz $f_{0}$ selbst ist in $x(t)$ nicht enthalten, lediglich ganzzahlige Vielfache davon, nämlich $f_{1} = 500\; {\rm Hz}$ und $f_{2} = 200\; {\rm Hz}$.
Mit dem interaktiven Applet Periodendauer periodischer Signale lässt sich die resultierende Periodendauer zweier harmonischer Schwingungen ermitteln.
Aufgaben zum Kapitel