Difference between revisions of "Aufgaben:Exercise 2.4: 2D Transfer Function"
m (Guenter moved page Exercise 2.4: 2-D Transfer Function to Exercise 2.4: 2D Transfer Function) |
|||
| Line 4: | Line 4: | ||
[[File:P_ID2161__Mob_A_2_4.png|right|frame|2D impulse response $|h(\tau, \hspace{0.05cm}t)|$]] | [[File:P_ID2161__Mob_A_2_4.png|right|frame|2D impulse response $|h(\tau, \hspace{0.05cm}t)|$]] | ||
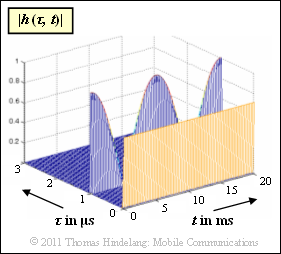
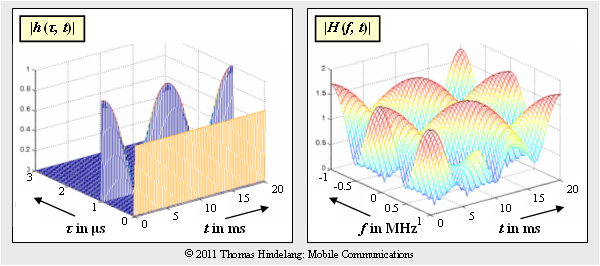
The graph shows the two-dimensional impulse response $h(\tau, \hspace{0.05cm}t)$ of a mobile radio system in magnitude representation. | The graph shows the two-dimensional impulse response $h(\tau, \hspace{0.05cm}t)$ of a mobile radio system in magnitude representation. | ||
| − | *It can be seen that the 2D | + | *It can be seen that the 2D impulse response only has components at delays $\tau = 0$ and $\tau = 1 \ \rm µ s$ . |
*At these times: | *At these times: | ||
| − | $$h(\tau = 0\,{\rm µ s},\hspace{0.05cm}t) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \frac{1}{ \sqrt{2}} = {\rm const.}$$ | + | :$$h(\tau = 0\,{\rm µ s},\hspace{0.05cm}t) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \frac{1}{ \sqrt{2}} = {\rm const.}$$ |
| − | $$h(\tau = 1\,{\rm µ s},\hspace{0.05cm}t) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \cos(2\pi \cdot {t}/{ T_0})\hspace{0.05cm}.$$ | + | :$$h(\tau = 1\,{\rm µ s},\hspace{0.05cm}t) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \cos(2\pi \cdot {t}/{ T_0})\hspace{0.05cm}.$$ |
| − | For all other values of $\tau$, we have $h(\tau, \hspace{0.05cm}t) \equiv 0$. | + | For all other values of $\tau$, we have $h(\tau, \hspace{0.05cm}t) \equiv 0$. |
We want to obtain the two-dimensional transfer function $H(f, \hspace{0.05cm} t)$ as the Fourier transform of $h(\tau, t)$ with respect to the delay $\tau$: | We want to obtain the two-dimensional transfer function $H(f, \hspace{0.05cm} t)$ as the Fourier transform of $h(\tau, t)$ with respect to the delay $\tau$: | ||
| Line 15: | Line 15: | ||
\hspace{0.2cm} \stackrel {f,\hspace{0.05cm}\tau}{\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ} \hspace{0.2cm} h(\tau,\hspace{0.05cm}t) | \hspace{0.2cm} \stackrel {f,\hspace{0.05cm}\tau}{\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ} \hspace{0.2cm} h(\tau,\hspace{0.05cm}t) | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| + | |||
| + | |||
''Notes:'' | ''Notes:'' | ||
* This task belongs to chapter [[Mobile_Communications/Multi-Path_Reception_in_Mobile_Communications| Multi–Path Reception in Mobile Communications]]. | * This task belongs to chapter [[Mobile_Communications/Multi-Path_Reception_in_Mobile_Communications| Multi–Path Reception in Mobile Communications]]. | ||
| − | * A similar problem is treated in [[Aufgaben:Exercise_2.5:_Scatter_Function| | + | * A similar problem is treated in [[Aufgaben:Exercise_2.5:_Scatter_Function| Exercize 2.5]] but with a different nomenclature. |
| Line 27: | Line 29: | ||
===Questionnaire=== | ===Questionnaire=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {What is the period $T_0$ of the function $h(\tau = 1 \ {\rm µ s},\hspace{0.05cm} t)$? Note that the graph shows the <u>magnitude</u> $|h(\tau, \hspace{0.05cm}t)|$ . | + | {What is the period $T_0$ of the function $h(\tau = 1 \ {\rm µ s},\hspace{0.05cm} t)$? Note that the graph shows the <u>magnitude</u> $|h(\tau, \hspace{0.05cm}t)|$ . |
|type="{}"} | |type="{}"} | ||
$T_0 \ = \ ${ 20 3% } $\ \ \rm ms$ | $T_0 \ = \ ${ 20 3% } $\ \ \rm ms$ | ||
| − | {At what times $t_1$ $($between $0$ and $10 \ \rm ms)$ and $t_2$ $($between $10 \ \ \rm ms$ and $20 \ \ \rm ms)$ is $H(f, \hspace{0.05cm}t)$ constant in | + | {At what times $t_1$ $($between $0$ and $10 \ \rm ms)$ and $t_2$ $($between $10 \ \ \rm ms$ and $20 \ \ \rm ms)$ is $H(f, \hspace{0.05cm}t)$ constant in $f$ ? |
|type="{}"} | |type="{}"} | ||
$t_1 \ = \ ${ 5 3% } $\ \ \rm ms$ | $t_1 \ = \ ${ 5 3% } $\ \ \rm ms$ | ||
$t_2 \ = \ ${ 15 3% } $\ \ \rm ms$ | $t_2 \ = \ ${ 15 3% } $\ \ \rm ms$ | ||
| − | {Calculate $H_0(f) = H(f, \hspace{0.05cm}t = 0)$. Which statements are true? | + | {Calculate $H_0(f) = H(f, \hspace{0.05cm}t = 0)$. Which statements are true? |
|type="[]"} | |type="[]"} | ||
| − | + We have $H_0(f) = H_0(f + i \cdot 1 \ {\rm MHz}), \ i = ±1, ±2, \ \ \text{...}$ | + | + We have $H_0(f) = H_0(f + i \cdot 1 \ {\rm MHz}), \ i = ±1, ±2, \ \ \text{...}$ |
+ We have approximately $0.293 ≤ |H_0(f)| ≤ 1.707$. | + We have approximately $0.293 ≤ |H_0(f)| ≤ 1.707$. | ||
| − | + $|H_0(f)|$ has a maximum at | + | + $|H_0(f)|$ has a maximum at $f = 0$ . |
| − | {Calculate $H_{10}(f) = H(f, \hspace{0.05cm}t = 10 \ \rm ms)$. Which statements are true? | + | {Calculate $H_{10}(f) = H(f, \hspace{0.05cm}t = 10 \ \rm ms)$. Which statements are true? |
|type="[]"} | |type="[]"} | ||
| − | + We have $H_{10}(f) = H_{10}(f + i \cdot 1 \ {\rm MHz}),\ i = ±1, ±2, \ \ \text{...}$ | + | + We have $H_{10}(f) = H_{10}(f + i \cdot 1 \ {\rm MHz}),\ i = ±1, ±2, \ \ \text{...}$ |
+ We have approximately $0.293 ≤ H_{10}(f) ≤ 1.707$. | + We have approximately $0.293 ≤ H_{10}(f) ≤ 1.707$. | ||
| − | - $|H_{10}(f)|$ has a maximum at | + | - $|H_{10}(f)|$ has a maximum at $f = 0$ . |
</quiz> | </quiz> | ||
Revision as of 17:04, 11 January 2021
The graph shows the two-dimensional impulse response $h(\tau, \hspace{0.05cm}t)$ of a mobile radio system in magnitude representation.
- It can be seen that the 2D impulse response only has components at delays $\tau = 0$ and $\tau = 1 \ \rm µ s$ .
- At these times:
- $$h(\tau = 0\,{\rm µ s},\hspace{0.05cm}t) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \frac{1}{ \sqrt{2}} = {\rm const.}$$
- $$h(\tau = 1\,{\rm µ s},\hspace{0.05cm}t) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \cos(2\pi \cdot {t}/{ T_0})\hspace{0.05cm}.$$
For all other values of $\tau$, we have $h(\tau, \hspace{0.05cm}t) \equiv 0$.
We want to obtain the two-dimensional transfer function $H(f, \hspace{0.05cm} t)$ as the Fourier transform of $h(\tau, t)$ with respect to the delay $\tau$:
- $$H(f,\hspace{0.05cm} t) \hspace{0.2cm} \stackrel {f,\hspace{0.05cm}\tau}{\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ} \hspace{0.2cm} h(\tau,\hspace{0.05cm}t) \hspace{0.05cm}.$$
Notes:
- This task belongs to chapter Multi–Path Reception in Mobile Communications.
- A similar problem is treated in Exercize 2.5 but with a different nomenclature.
Questionnaire
Solution
(2) At time $t_1 \ \underline {= 5 \ \ \rm ms}$ we have $h(\tau = 1 \ {\rm µ s}, t_1) = 0$. Accordingly, the following applies
- $$h(\tau = 1\,{\rm µ s},\hspace{0.05cm}t_1) = \frac{1}{ \sqrt{2}} \cdot \delta(\tau)\hspace{0.3cm}\Rightarrow \hspace{0.3cm} H(f,\hspace{0.05cm}t_1) = \frac{1}{ \sqrt{2}} = {\rm const.}$$
The same applies to $t_2 \ \underline {= 15 \ \ \rm ms}$:
- $$h(\tau = 1\,{\rm µ s},\hspace{0.05cm}t_2) = \frac{1}{ \sqrt{2}} \cdot \delta(\tau)\hspace{0.3cm}\Rightarrow \hspace{0.3cm} H(f,\hspace{0.05cm}t_2) = \frac{1}{ \sqrt{2}} = {\rm const.}$$
(3) At time $t = 0$ the impulse response with $\tau_1 = 1 \ \ \rm µ s$ is
- $$h(\tau,\hspace{0.05cm}t = 0) = \frac{1}{ \sqrt{2}} \cdot \delta(\tau)+ \delta(\tau - \tau_1)\hspace{0.05cm}.$$
Its Fourier transform is
- $$H_0(f) = H(f,\hspace{0.05cm}t = 0) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \frac{1}{ \sqrt{2}} + 1 \cdot {\rm e}^{- {\rm j}\cdot 2 \pi f \tau_1}=\frac{1}{ \sqrt{2}} + \cos( 2 \pi f \tau_1)- {\rm j}\cdot \sin( 2 \pi f \tau_1)$$
- $$\Rightarrow \hspace{0.3cm} |H_0(f)| \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \sqrt { \left [ {1}/{ \sqrt{2}} + \cos( 2 \pi f \tau_1) \right ]^2 + \left [\sin( 2 \pi f \tau_1)\right ]^2}= \sqrt { 0.5 + 1 + {2}/{ \sqrt{2}} \cdot \cos( 2 \pi f \tau_1)} = \sqrt { 1.5 + { \sqrt{2}} \cdot \cos( 2 \pi f \tau_1)}\hspace{0.05cm}.$$
Therefore,
- $H_0(f)$ is periodic with $1/\tau_1 = 1 \ \rm MHz$.
- For the maximum and minimum values, we have
- $${\rm Max}\, \left [ \, |H_0(f)|\, \right ] \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \sqrt { 1.5 + { \sqrt{2}} } \approx 1.707 \hspace{0.05cm},\hspace{0.5cm}{\rm Min}\, \left [ \, |H_0(f)|\, \right ] \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \sqrt { 1.5 - { \sqrt{2}} } \approx 0.293 \hspace{0.05cm}. $$
- At $f = 0$, $|H_0(f)|$ has a maximum.
Therefore, all three solution suggestions are correct.
(4) For the time $t = 10 \ \rm ms$ the following equations apply:
- $$h(\tau,\hspace{0.05cm}t = 10\,{\rm ms}) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \frac{1}{ \sqrt{2}} \cdot \delta(\tau)- \delta(\tau - \tau_1)\hspace{0.05cm},$$
- $$H_{10}(f) = H(f,\hspace{0.05cm}t = 10\,{\rm ms}) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \frac{1}{ \sqrt{2}} - \cos( 2 \pi f \tau_1)+ {\rm j}\cdot \sin( 2 \pi f \tau_1)\hspace{0.05cm},$$
- $$ |H_{10}(f)| \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \sqrt { 1.5 - { \sqrt{2}} \cdot \cos( 2 \pi f \tau_1)}\hspace{0.05cm}.$$
Solutions 1 and 2 are correct:
- The frequency period does not change from $t = 0$.
- The maximum value is still $1,707$ and the minimum value $0,293$ does not change compared to the subtask (3).
- For $f = 0$ there is now a minimum and not a maximum.
The graph on the right shows the magnitude $|H(f, t)|$ of the 2D transfer function.