Difference between revisions of "Aufgaben:Exercise 3.6: Even and Odd Time Signals"
m (Oezdemir moved page Aufgabe 3.6: Gerades/ungerades Zeitsignal to Exercise 3.6: Even/Odd Time Signal) |
|||
| Line 5: | Line 5: | ||
[[File:P_ID516__Sig_A_3_6_neu.png|250px|right|frame|„Keilfunktion” sowie ein gerades und ein ungerades Zeitsignal]] | [[File:P_ID516__Sig_A_3_6_neu.png|250px|right|frame|„Keilfunktion” sowie ein gerades und ein ungerades Zeitsignal]] | ||
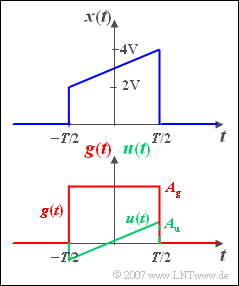
| − | + | We are looking for the spectrum $X(f)$ of the pulse-shaped signal $x(t)$ sketched opposite, which rises linearly from $2\,\text{ V}$ to $4\,\text{ V}$ in the range from $–T/2$ to $+T/2$ and is zero outside. | |
| − | + | The spectral functions of the signals $g(t)$ and $u(t)$ shown below are assumed to be known: | |
| − | * | + | *The even, rectangular time function $g(t)$ has the spectrum |
:$$G( f ) = A_g \cdot T \cdot {\mathop{\rm si}\nolimits}( { {\rm{\pi }}fT} ) \hspace{0.3cm} {\rm{mit}}\hspace{0.3cm} {\mathop{\rm si}\nolimits}( x ) = {\sin ( x )}/{x}.$$ | :$$G( f ) = A_g \cdot T \cdot {\mathop{\rm si}\nolimits}( { {\rm{\pi }}fT} ) \hspace{0.3cm} {\rm{mit}}\hspace{0.3cm} {\mathop{\rm si}\nolimits}( x ) = {\sin ( x )}/{x}.$$ | ||
| − | * | + | *The spectrum of the asymmetric function $u(t)$ is: |
:$$U( f ) = - {\rm{j}} \cdot \frac{ {A_u \cdot T}}{ {2{\rm{\pi }}fT}}\big[ {{\mathop{\rm si}\nolimits} ( { {\rm{\pi }}fT} ) - \cos ( { {\rm{\pi }}fT} )} \big].$$ | :$$U( f ) = - {\rm{j}} \cdot \frac{ {A_u \cdot T}}{ {2{\rm{\pi }}fT}}\big[ {{\mathop{\rm si}\nolimits} ( { {\rm{\pi }}fT} ) - \cos ( { {\rm{\pi }}fT} )} \big].$$ | ||
| Line 23: | Line 23: | ||
| − | '' | + | ''Hints:'' |
| − | * | + | *This exercise belongs to the chapter [[Signal_Representation/Fourier_Transform_Laws|Fourier Transform Laws]]. |
| − | * | + | *All of these laws are illustrated with examples in the learning video [[Gesetzmäßigkeiten_der_Fouriertransformation_(Lernvideo)|Gesetzmäßigkeiten der Fouriertransformation]] . |
| − | * | + | *Solve this task with the help of the [[Signal_Representation/Fourier_Transform_Laws#Mapping_theorem|mapping theorem]]. |
| − | * | + | *Use the signal parameters $A_u = 1\,\text{ V}$ and $T = 1\,\text{ ms}$ for the first two subtasks. |
| − | === | + | ===Questions=== |
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Calculate the (purely imaginary) spectral values of the unbalanced signal $u(t)$ at the frequencies $f = 0.5\,\text{kHz}$ and $f = 1\,\text{kHz}$. |
|type="{}"} | |type="{}"} | ||
${\rm Im}\big[U(f=0.5 \,\text{kHz})\big] \ = \ $ { -0.205--0.195 } $\text{mV/Hz}$ | ${\rm Im}\big[U(f=0.5 \,\text{kHz})\big] \ = \ $ { -0.205--0.195 } $\text{mV/Hz}$ | ||
${\rm Im}\big[U(f=1.0 \,\text{kHz})\big]\ = \ $ { 0.159 3% } $\text{mV/Hz}$ | ${\rm Im}\big[U(f=1.0 \,\text{kHz})\big]\ = \ $ { 0.159 3% } $\text{mV/Hz}$ | ||
| − | { | + | {What is the spectral value of $u(t)$ at the frequency $f = 0$? |
| − | '' | + | ''Hint'': Think before you calculate. |
|type="{}"} | |type="{}"} | ||
${\rm Im}\big[U(f=0)\big]\ = \ $ { 0. } $\text{mV/Hz}$ | ${\rm Im}\big[U(f=0)\big]\ = \ $ { 0. } $\text{mV/Hz}$ | ||
| − | { | + | {Using the result from '''(1)''' calculate the spectral value of the signal $x(t)$ at the frequency $f=0.5 \,\text{kHz}$. |
|type="{}"} | |type="{}"} | ||
${\rm Re}\big[X(f=0.5 \,\text{kHz})\big]\ = \ $ { 1.91 3% } $\text{mV/Hz}$ | ${\rm Re}\big[X(f=0.5 \,\text{kHz})\big]\ = \ $ { 1.91 3% } $\text{mV/Hz}$ | ||
| Line 53: | Line 53: | ||
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' For $f \cdot T = 0.5$ one obtains from the given equation: |
:$$U( {f = 0.5\;{\rm{kHz}}} ) = - {\rm{j}} \cdot \frac{ {A_u \cdot T}}{ {\rm{\pi }}} \cdot {\mathop{\rm si}\nolimits} ( {{ {\rm{\pi }}}/{2}} ) = - {\rm{j}} \cdot \frac{2}{ { {\rm{\pi }}^{\rm{2}} }} \cdot A_{\rm u} \cdot T.$$ | :$$U( {f = 0.5\;{\rm{kHz}}} ) = - {\rm{j}} \cdot \frac{ {A_u \cdot T}}{ {\rm{\pi }}} \cdot {\mathop{\rm si}\nolimits} ( {{ {\rm{\pi }}}/{2}} ) = - {\rm{j}} \cdot \frac{2}{ { {\rm{\pi }}^{\rm{2}} }} \cdot A_{\rm u} \cdot T.$$ | ||
| − | * | + | *The imaginary part is numerically ${\rm Im}[U(f=0.5 \,\text{kHz})]\; \underline{\approx 0.2 \,\text{mV/Hz}}$. |
| − | * | + | *In contrast, the si function at $f \cdot T = 1$ yields the value zero, while the cosine is equal to $-1$ . Thus, with $A_u = 1\,\text{V}$ and $T = 1\,\text{ms}$ one obtains: |
:$$U( {f = 1\;{\rm{kHz}}} ) = {\rm{j}} \cdot \frac{ {A_{\rm u} \cdot T}}{ { {\rm{2\pi }}}} \hspace{0.3 cm} \Rightarrow \hspace{0.3 cm} {\rm Re} [\text{...}] \hspace{0.15 cm}\underline{ = 0}, \hspace{0.3 cm}{\rm Im} [\text{...}] \hspace{0.15 cm}\underline{\approx 0.159 \;{\rm{mV/Hz}}}.$$ | :$$U( {f = 1\;{\rm{kHz}}} ) = {\rm{j}} \cdot \frac{ {A_{\rm u} \cdot T}}{ { {\rm{2\pi }}}} \hspace{0.3 cm} \Rightarrow \hspace{0.3 cm} {\rm Re} [\text{...}] \hspace{0.15 cm}\underline{ = 0}, \hspace{0.3 cm}{\rm Im} [\text{...}] \hspace{0.15 cm}\underline{\approx 0.159 \;{\rm{mV/Hz}}}.$$ | ||
| Line 67: | Line 67: | ||
| − | '''(2)''' | + | '''(2)''' According to the mapping theorem, an odd time function $u(t)$ always has an imaginary and at the same time odd spectrum |
| − | $U( { - f} ) = - U( f ).$ | + | $U( { - f} ) = - U( f ).$ With the boundary transition $f \rightarrow \infty$ follows from the given equation |
:$$U( f ) = - {\rm{j}} \cdot \frac{ {A_u \cdot T}}{ {2{\rm{\pi }}fT}}\big[ { {\mathop{\rm si}\nolimits} ( {{\rm{\pi }}fT} ) - \cos ( { {\rm{\pi }}fT} )} \big]$$ | :$$U( f ) = - {\rm{j}} \cdot \frac{ {A_u \cdot T}}{ {2{\rm{\pi }}fT}}\big[ { {\mathop{\rm si}\nolimits} ( {{\rm{\pi }}fT} ) - \cos ( { {\rm{\pi }}fT} )} \big]$$ | ||
| − | + | the result $U(f = 0) = 0$. Formally, one could confirm this result by applying l'Hospital's rule. | |
| − | + | We proceed a little more pragmatically. | |
| − | * | + | *For example, if we set $f \cdot T = 0.01$, we obtain: |
| − | + | $$U( {f \cdot T = 0.01}) = -{\rm{j}} \cdot \frac{ {A_{\rm u} \cdot T}}{{0.02{\rm{\pi }}}}\big[ {{\mathop{\rm si}\nolimits} ( {0.01{\rm{\pi }}} ) - \cos ( {0.01{\rm{\pi }}} )} \big ] = - {\rm{j}} \cdot \frac{ {A{\rm u} \cdot T}}{{0.02{\rm{\pi }}}}( {0.999836 - 0.999507} ) \approx - {\rm{j}} \cdot 5 \cdot 10^{ - 6} \;{\rm{V/Hz}}{\rm{.}}$$ | |
| − | * | + | *For even smaller frequency values, the result also becomes smaller and smaller. |
| − | * | + | *You get to the result $U(f = 0)\;\underline{ = 0}$, more quickly if you take into account that the integral over $u(t)$ disappears. |
| − | * | + | *So you don't have to calculate at all. |
| − | '''(3)''' | + | '''(3)''' The signal $x(t)$ can be divided into the even and the odd part, which lead to the even real part and the odd imaginary part of $X(f)$ : |
| − | * | + | *The even part is equal to the function $g(t)$ with $A_g = 3\,\text{V}$. From this follows for the real part of the spectral value at $f \cdot T = 0.5$: |
:$${\mathop{\rm Re}\nolimits} \left[ {X( {f \cdot T = 0.5} )} \right] = A_{\rm g} \cdot T \cdot {\mathop{\rm si}\nolimits} ( {{ {\rm{\pi }}}/{2}} ) \hspace{0.15 cm}\underline{= 1.91 \;{\rm{mV/Hz}}}{\rm{.}}$$ | :$${\mathop{\rm Re}\nolimits} \left[ {X( {f \cdot T = 0.5} )} \right] = A_{\rm g} \cdot T \cdot {\mathop{\rm si}\nolimits} ( {{ {\rm{\pi }}}/{2}} ) \hspace{0.15 cm}\underline{= 1.91 \;{\rm{mV/Hz}}}{\rm{.}}$$ | ||
| − | * | + | *The imaginary part results from the spectral function $U(f)$ with $A_u = 1\,\text{V}$. This was already calculated in subtask '''(1)''' : |
:$${\mathop{\rm Im}\nolimits} \left[ {X( {f \cdot T = 0.5} )} \right] \hspace{0.15 cm}\underline{\approx - 0.2 \;{\rm{mV/Hz}}}{\rm{.}}$$ | :$${\mathop{\rm Im}\nolimits} \left[ {X( {f \cdot T = 0.5} )} \right] \hspace{0.15 cm}\underline{\approx - 0.2 \;{\rm{mV/Hz}}}{\rm{.}}$$ | ||
Revision as of 18:36, 27 January 2021
We are looking for the spectrum $X(f)$ of the pulse-shaped signal $x(t)$ sketched opposite, which rises linearly from $2\,\text{ V}$ to $4\,\text{ V}$ in the range from $–T/2$ to $+T/2$ and is zero outside.
The spectral functions of the signals $g(t)$ and $u(t)$ shown below are assumed to be known:
- The even, rectangular time function $g(t)$ has the spectrum
- $$G( f ) = A_g \cdot T \cdot {\mathop{\rm si}\nolimits}( { {\rm{\pi }}fT} ) \hspace{0.3cm} {\rm{mit}}\hspace{0.3cm} {\mathop{\rm si}\nolimits}( x ) = {\sin ( x )}/{x}.$$
- The spectrum of the asymmetric function $u(t)$ is:
- $$U( f ) = - {\rm{j}} \cdot \frac{ {A_u \cdot T}}{ {2{\rm{\pi }}fT}}\big[ {{\mathop{\rm si}\nolimits} ( { {\rm{\pi }}fT} ) - \cos ( { {\rm{\pi }}fT} )} \big].$$
Hints:
- This exercise belongs to the chapter Fourier Transform Laws.
- All of these laws are illustrated with examples in the learning video Gesetzmäßigkeiten der Fouriertransformation .
- Solve this task with the help of the mapping theorem.
- Use the signal parameters $A_u = 1\,\text{ V}$ and $T = 1\,\text{ ms}$ for the first two subtasks.
Questions
Solution
- $$U( {f = 0.5\;{\rm{kHz}}} ) = - {\rm{j}} \cdot \frac{ {A_u \cdot T}}{ {\rm{\pi }}} \cdot {\mathop{\rm si}\nolimits} ( {{ {\rm{\pi }}}/{2}} ) = - {\rm{j}} \cdot \frac{2}{ { {\rm{\pi }}^{\rm{2}} }} \cdot A_{\rm u} \cdot T.$$
- The imaginary part is numerically ${\rm Im}[U(f=0.5 \,\text{kHz})]\; \underline{\approx 0.2 \,\text{mV/Hz}}$.
- In contrast, the si function at $f \cdot T = 1$ yields the value zero, while the cosine is equal to $-1$ . Thus, with $A_u = 1\,\text{V}$ and $T = 1\,\text{ms}$ one obtains:
- $$U( {f = 1\;{\rm{kHz}}} ) = {\rm{j}} \cdot \frac{ {A_{\rm u} \cdot T}}{ { {\rm{2\pi }}}} \hspace{0.3 cm} \Rightarrow \hspace{0.3 cm} {\rm Re} [\text{...}] \hspace{0.15 cm}\underline{ = 0}, \hspace{0.3 cm}{\rm Im} [\text{...}] \hspace{0.15 cm}\underline{\approx 0.159 \;{\rm{mV/Hz}}}.$$
(2) According to the mapping theorem, an odd time function $u(t)$ always has an imaginary and at the same time odd spectrum $U( { - f} ) = - U( f ).$ With the boundary transition $f \rightarrow \infty$ follows from the given equation
- $$U( f ) = - {\rm{j}} \cdot \frac{ {A_u \cdot T}}{ {2{\rm{\pi }}fT}}\big[ { {\mathop{\rm si}\nolimits} ( {{\rm{\pi }}fT} ) - \cos ( { {\rm{\pi }}fT} )} \big]$$
the result $U(f = 0) = 0$. Formally, one could confirm this result by applying l'Hospital's rule.
We proceed a little more pragmatically.
- For example, if we set $f \cdot T = 0.01$, we obtain:
$$U( {f \cdot T = 0.01}) = -{\rm{j}} \cdot \frac{ {A_{\rm u} \cdot T}}{{0.02{\rm{\pi }}}}\big[ {{\mathop{\rm si}\nolimits} ( {0.01{\rm{\pi }}} ) - \cos ( {0.01{\rm{\pi }}} )} \big ] = - {\rm{j}} \cdot \frac{ {A{\rm u} \cdot T}}{{0.02{\rm{\pi }}}}( {0.999836 - 0.999507} ) \approx - {\rm{j}} \cdot 5 \cdot 10^{ - 6} \;{\rm{V/Hz}}{\rm{.}}$$
- For even smaller frequency values, the result also becomes smaller and smaller.
- You get to the result $U(f = 0)\;\underline{ = 0}$, more quickly if you take into account that the integral over $u(t)$ disappears.
- So you don't have to calculate at all.
(3) The signal $x(t)$ can be divided into the even and the odd part, which lead to the even real part and the odd imaginary part of $X(f)$ :
- The even part is equal to the function $g(t)$ with $A_g = 3\,\text{V}$. From this follows for the real part of the spectral value at $f \cdot T = 0.5$:
- $${\mathop{\rm Re}\nolimits} \left[ {X( {f \cdot T = 0.5} )} \right] = A_{\rm g} \cdot T \cdot {\mathop{\rm si}\nolimits} ( {{ {\rm{\pi }}}/{2}} ) \hspace{0.15 cm}\underline{= 1.91 \;{\rm{mV/Hz}}}{\rm{.}}$$
- The imaginary part results from the spectral function $U(f)$ with $A_u = 1\,\text{V}$. This was already calculated in subtask (1) :
- $${\mathop{\rm Im}\nolimits} \left[ {X( {f \cdot T = 0.5} )} \right] \hspace{0.15 cm}\underline{\approx - 0.2 \;{\rm{mV/Hz}}}{\rm{.}}$$