Difference between revisions of "Signal Representation/Special Cases of Pulses"
m (Text replacement - "low pass" to "low-pass") |
|||
| Line 30: | Line 30: | ||
:$${\rm si}\hspace{-0.08cm}\left( x \right) = \sin \left( x \right)/x.$$}} | :$${\rm si}\hspace{-0.08cm}\left( x \right) = \sin \left( x \right)/x.$$}} | ||
| + | |||
| + | '''Zusätzlich:''' | ||
| + | |||
| + | :$${\rm sinc}\hspace{-0.08cm}( x ) = \frac {\sin (\pi x) }{\pi x }.$$ | ||
| Line 35: | Line 39: | ||
:$$X( f ) = A \cdot T \cdot {\rm si}\hspace{-0.08cm}\left( {\pi fT} \right).$$ | :$$X( f ) = A \cdot T \cdot {\rm si}\hspace{-0.08cm}\left( {\pi fT} \right).$$ | ||
| + | |||
| + | '''Zusätzlich:''' | ||
| + | |||
| + | :$$X( f ) = A \cdot T \cdot {\rm sinc}\hspace{-0.08cm}\left( {fT} \right).$$ | ||
As the graphic shows, $X(f)$ has the following properties: | As the graphic shows, $X(f)$ has the following properties: | ||
Revision as of 14:43, 28 January 2021
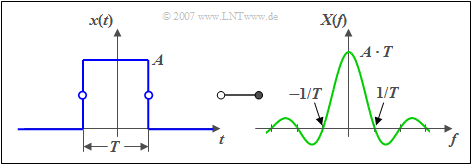
Rectangular Impulse
One speaks of a 'rectangle-pulse, if the following applies for the time domain:
- $$x(t) = \left\{ \begin{array}{l} \hspace{0.25cm}A \\ A /2 \\ \hspace{0.25cm} 0 \\ \end{array} \right.\quad \quad \begin{array}{*{20}c} {\rm{for}} \\ {\rm{for}} \\ {\rm{for}} \\ \end{array}\begin{array}{*{20}c} {\left| \hspace{0.05cm} t\hspace{0.05cm} \right| < T/2,} \\ {\left| \hspace{0.05cm}t\hspace{0.05cm} \right| = T/2,} \\ {\left|\hspace{0.05cm} t \hspace{0.05cm} \right| > T/2.} \\ \end{array}$$
$A$ denotes the amplitude of the pulse and $T$ the pulse duration.
The corresponding spectral function $X(f)$ is obtained by using the first Fourier integral:
- $$X(f) = \int_{ - T/2}^{+T/2} {A \cdot {\rm e}^{ -{\rm j}2\pi ft}\, {\rm d}t = A }\cdot \int_{ - T/2}^{+T/2} {\cos ( {2\pi}ft )\,{\rm d}t - {\rm j} \cdot A} \int_{ - T/2}^{+T/2} {\sin ( {2\pi ft} )}\,{\rm d}t .$$
- Here the integration limits $\pm T/2$ take into account that $x(t)$ is identical to zero outside the interval from $-T/2$ to $+T/2$ .
- The second integral disappears due to the odd integrand and you get
- $$X(f) = \frac{A \cdot \sin \left( {\pi fT} \right)}{\pi f}.$$
$\text{Definition:}$ For abbreviation we define the following function and call it si-function or also as splitting function:
- $${\rm si}\hspace{-0.08cm}\left( x \right) = \sin \left( x \right)/x.$$
Zusätzlich:
- $${\rm sinc}\hspace{-0.08cm}( x ) = \frac {\sin (\pi x) }{\pi x }.$$
By extending the numerator and denominator each with $T$ one can also write for the spectral function of the rectangular pulse:
- $$X( f ) = A \cdot T \cdot {\rm si}\hspace{-0.08cm}\left( {\pi fT} \right).$$
Zusätzlich:
- $$X( f ) = A \cdot T \cdot {\rm sinc}\hspace{-0.08cm}\left( {fT} \right).$$
As the graphic shows, $X(f)$ has the following properties:
- The maximum is at frequency $f=0$ and has the value $A \cdot T$ (area of the rectangle).
- For the frequencies $f_n = n/T$ with $n = ±1, ±2, ±3,\text{ ...} $ has the spectrum zeroes:
- $$X( {f = f_n } ) = 0.$$
- The following constraint applies to the magnitude spectrum:
- $$\left| {X( f )} \right| \le \frac{A}{\pi \cdot \left| f \right|}.$$
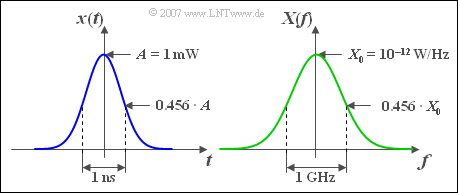
Gaussian Impulse
Another example of an aperiodic signal is the Gaussian pulse with the time
- $$x(t) = A \cdot {\rm e}^{ - \pi \left( {t/\Delta t} \right)^2 } .$$
This pulse is described by two parameters, namely
- the pulse amplitude $A$, and
- the equivalent pulse duration $\Delta t$.
$\text{Definition:}$ The term equivalent pulse duration is generally used to describe the duration of a rectangular pulse with the same amplitude and area as the given pulse-shaped signal $x(t)$:
- $$\Delta t = \frac{1}{A }\cdot \hspace{-0.15cm} \int_{ - \infty }^{ + \infty } {x( t )\, {\rm d}t.}$$
The Gaussian pulse $x(t)$ has the following properties $($see graphic in $\text{Example 1})$:
- The time function is for all times from $-\infty$ to $+\infty$ existent and positive.
- This means simultaneously: The absolute impulse duration is infinite.
- The pulse maximum $A$ is $t = 0$.
- At $t = \pm \Delta t/2$ , the impulse is decayed to $\text{e}^{-\pi/4} \approx 0.456$ of the Maximum. And at $t = \pm \Delta t$ , the signal value is less than $3.5 \cdot 10^{-6} \cdot A$.
- The spectral function $X(f)$ is also gaussian and has the same properties as the gaussian pulse $x(t)$:
- $$X(f) = A \cdot \Delta t \cdot {\rm e}^{ - \pi \left( {f \cdot \Delta t} \right)^2 }.$$
On the page reciprocity theorem the analogies of time domain and frequency domain of the Gaussian pulse are discussed in detail.
The following example illustrates the similarities and differences between the Gaussian pulse $x(t)$ and its spectrum $X(f)$
{{GraueBox|TEXT= $\text{Example 1:}$ The output power pulse $x(t)$ of a laser for digital optical transmission can be assumed to be Gaussian in the equivalent low-pass range with good approximation.
Let the signal parameters be $A = 1 \,\text{mW}$ and $\Delta t =1 \,\text{ns}$.
Damit erhält man im Spektralbereich die vergleichbaren Kenngrößen:
- das Maximum $X_0 = X(f=0) = A \cdot \Delta t = 10^{-12} \,\text{W/Hz}$,
- the equivalent bandwidth $\Delta f = 1/\Delta t = 1 \,\text{GHz}$.
Theoretically, the absolute frequency band extends to infinity. However, at $f = 2 \cdot \delta f = 2\,\text{GHz}$ the spectral function is already reduced by the factor $3.5 \cdot 10^{-6}$ compared to its maximum.}
We would like to draw your attention to two interactive applets on this topic with which you can display the time and frequency domain representations of the Gaussian pulse, rectangular pulse, triangular pulse, trapezoidal pulse and cosine rolloff pulse or the comparable quantities of an LZI–system parameterized:
It is also possible to display the so-called "dual correspondences".
Dirac Delta Impulse
In the chapter Periodic Signals the Dirac Function was already used to describe the spectrum of a DC signal or a harmonic oscillation.
However, in communications engineering it is also common and extremely advantageous to describe and analyze short-term impulse-like processes with the help of this mathematical function in the time domain.
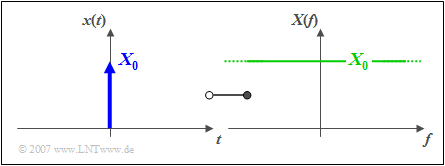
$\text{Definition:}$ One calls as Diracimpuls the time response
- $$x(t) = X_0 \cdot \delta (t),$$
which can be characterised as follows (see plot):
- The Dirac-pulse is infinitely narrow ⇒ it holds $x(t)$ = 0 for $t \neq 0$ and at time $t = 0$ the Dirac-pulse is infinitely high.
- I f $x(t)$ describes a voltage curve, so the pulse weight $X_0$ has the unit "Vs" (i.e. the unit "V/Hz" of a spectral function), since $\delta (t)$ itself has the unit "1/s".
- The spectral function of the Dirac impulse includes all frequencies $f$ equally:
- $$X(f) = X_0 = \rm const.$$
The properties mentioned here are shown in the german learning video Derivation and Visualisation of the Dirac Function .
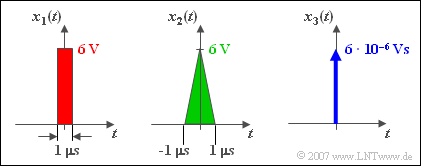
$\text{Example 2:}$ We consider a Network with low-pass–characteristic and very low cutoff frequency $f_{\rm G} = 10\,\text{ kHz}$. The output signal $y(t)$ does not (almost) change when one of the sketched signals $x_1(t)$, $x_2(t)$ or $x_3(t)$ is applied to the input.
This result can be interpreted as follows: equivalent pulse durations are the same in each case $(\Delta t = 1\, µ\text{s})$ and this is much smaller than $1/f_{\rm G} = 100 \, µ\text{s}$, the actual pulse shape (rectangle or triangle) has only a minor influence on the output signal $y(t)$.
- Both the rectangle $x_1(t)$ and the triangle $x_2(t)$ - can be approximated by the diraculse $x_3(t)$ .
- The impulse weight $X_0 = 6 - 10^{-6}\, \text{Vs}$ must be equal to the impulse areas of $x_1(t)$ and $x_2(t)$ . However, a sufficiently small cutoff frequency is required for this approximation. With $f_{\rm G} = 10 \, \text{MHz}$ ⇒ $1/f_{\rm G} = 100 \, \text{ns}$ this simplification would not be permitted.
- Even if the Dirac-pulse is drawn with the same height as the other two pulses, it still has an infinite value at the time $t = 0$ .
- The pulse area ("pulse weight") is always specified for the Dirac impulse. This differs from the other pulse amplitudes already in the unit (for example "Vs" instead of "V").
Exercises for the Chapter
Exercise 3.3: From The Signal to the Spectrum
Exercise 3.3Z: Rectangular- and Dirac Pulse